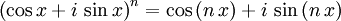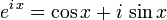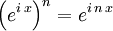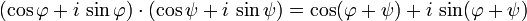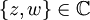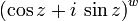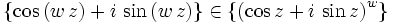Satz von De Moivre — Als Satz von De Moivre (nach Abraham de Moivre benannt) bezeichnet man: Satz von Moivre Laplace, Satz aus der Wahrscheinlichkeitstheorie über die Binomialverteilung Moivrescher Satz, Satz über die Beschreibung komplexer Zahlen Diese Seite … Deutsch Wikipedia
Formel von de Moivre — Der Moivresche Satz oder Satz von de Moivre, benannt nach Abraham de Moivre, besagt, dass für jede komplexe Zahl (und damit auch jede reelle Zahl) x und jede natürliche Zahl n der Zusammenhang gilt. Diese Formel verbindet die komplexen Zahlen mit … Deutsch Wikipedia
Satz von Moivre-Laplace — Plot der Dichte der Normalverteilung mit μ = 12 und σ = 3 und der Binomialverteilung mit n = 48 und p = 1/4 Der Satz von Moivre Laplace ist ein Satz aus der Wahrscheinlichkeitstheorie. Nach diesem Satz konvergiert die Binomialverteilung für … Deutsch Wikipedia
Moivrescher Satz — Der Moivresche Satz auch Satz von de Moivre oder Formel von de Moivre genannt, trägt seinen Namen zu Ehren von Abraham de Moivre[1], der diesen Satz im ersten Jahrzehnt des 18. Jahrhunderts fand.[2] Er besagt, dass für jede komplexe Zahl (und… … Deutsch Wikipedia
Moivre — [mwaːvr], Abraham de, französischer Mathematiker, * Vitry le François 26. 5. 1667, ✝ London 27. 11. 1754; emigrierte nach der Aufhebung des Edikts von Nantes (1685) nach England; Hauslehrer, später u. a. Mitglied der Royal Society. Moivre… … Universal-Lexikon
Moivre — (spr. mŭāwr ), Abraham de, Mathematiker, geb. 26. Mai 1667 in Vitry (Champagne), gest. 27. Nov. 1754 in London, wohin er als Hugenott 1687, nach Aufhebung des Edikts von Nantes (1685), geflohen war, und wo er sich durch Privatstunden ernährte.… … Meyers Großes Konversations-Lexikon
De Moivre — Abraham de Moivre Abraham de Moivre (* 26. Mai 1667 in Vitry le François; † 27. November 1754 in London) war ein französischer Mathematiker, der vor allem für den Satz von Moivre bekannt ist. Leben und Werk Moivre besuchte v … Deutsch Wikipedia
Abraham de Moivre — (* 26. Mai 1667 in Vitry le François; † 27. November 1754 in London) war ein französischer Mathematiker, der vor allem für den Satz von Moivre bekannt ist. Leben und Werk De Mo … Deutsch Wikipedia
Geschichte der Stochastik — Roulettespieler, um 1800. Das Glücksspiel war eine der frühesten Triebfedern der Wahrscheinlichkeitsrechnung … Deutsch Wikipedia
Geschichte der Wahrscheinlichkeitstheorie — Roulettespieler, um 1800. Das Glücksspiel war eine der frühesten Triebfedern der Wahrscheinlichkeitsrechnung … Deutsch Wikipedia
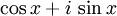 kann auch verkürzt als
kann auch verkürzt als 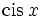 dargestellt werden.
dargestellt werden.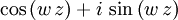 .
.