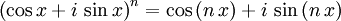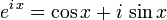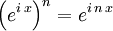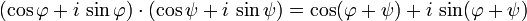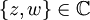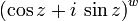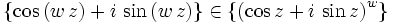Formel von Binet — Ein Kachelmuster aus Quadraten, deren Kantenlänge der Fiboncci Folge entspricht Die Fibonacci Folge ist eine unendliche Folge von Zahlen (den Fibonacci Zahlen), bei der sich die jeweils folgende Zahl durch Addition der beiden vorherigen Zahlen… … Deutsch Wikipedia
Satz von de Moivre — Der Moivresche Satz oder Satz von de Moivre, benannt nach Abraham de Moivre, besagt, dass für jede komplexe Zahl (und damit auch jede reelle Zahl) x und jede natürliche Zahl n der Zusammenhang gilt. Diese Formel verbindet die komplexen Zahlen mit … Deutsch Wikipedia
Cardanische Formel — Die cardanischen Formeln sind Formeln zur Lösung reduzierter kubischer Gleichungen (Gleichungen 3. Grades). Sie wurden, zusammen mit Lösungsformeln für quartische Gleichungen (Gleichungen 4. Grades), erstmals 1545 von dem Mathematiker Gerolamo… … Deutsch Wikipedia
De Moivre — Abraham de Moivre Abraham de Moivre (* 26. Mai 1667 in Vitry le François; † 27. November 1754 in London) war ein französischer Mathematiker, der vor allem für den Satz von Moivre bekannt ist. Leben und Werk Moivre besuchte v … Deutsch Wikipedia
Abraham de Moivre — (* 26. Mai 1667 in Vitry le François; † 27. November 1754 in London) war ein französischer Mathematiker, der vor allem für den Satz von Moivre bekannt ist. Leben und Werk De Mo … Deutsch Wikipedia
Moivrescher Satz — Der Moivresche Satz auch Satz von de Moivre oder Formel von de Moivre genannt, trägt seinen Namen zu Ehren von Abraham de Moivre[1], der diesen Satz im ersten Jahrzehnt des 18. Jahrhunderts fand.[2] Er besagt, dass für jede komplexe Zahl (und… … Deutsch Wikipedia
Fibonacci-Reihe — Ein Kachelmuster aus Quadraten, deren Kantenlänge der Fiboncci Folge entspricht Die Fibonacci Folge ist eine unendliche Folge von Zahlen (den Fibonacci Zahlen), bei der sich die jeweils folgende Zahl durch Addition der beiden vorherigen Zahlen… … Deutsch Wikipedia
Fibonacci-Zahl — Ein Kachelmuster aus Quadraten, deren Kantenlänge der Fiboncci Folge entspricht Die Fibonacci Folge ist eine unendliche Folge von Zahlen (den Fibonacci Zahlen), bei der sich die jeweils folgende Zahl durch Addition der beiden vorherigen Zahlen… … Deutsch Wikipedia
Fibonacci-Zahlen — Ein Kachelmuster aus Quadraten, deren Kantenlänge der Fiboncci Folge entspricht Die Fibonacci Folge ist eine unendliche Folge von Zahlen (den Fibonacci Zahlen), bei der sich die jeweils folgende Zahl durch Addition der beiden vorherigen Zahlen… … Deutsch Wikipedia
Fibonaccifolge — Ein Kachelmuster aus Quadraten, deren Kantenlänge der Fiboncci Folge entspricht Die Fibonacci Folge ist eine unendliche Folge von Zahlen (den Fibonacci Zahlen), bei der sich die jeweils folgende Zahl durch Addition der beiden vorherigen Zahlen… … Deutsch Wikipedia
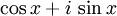 kann auch verkürzt als
kann auch verkürzt als 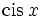 dargestellt werden.
dargestellt werden.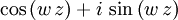 .
.