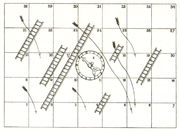
Snakes and Ladders

Leiterspiel oder weniger gebräuchlich Schlangen und Leitern (auf Englisch: Snakes and Ladders, in der Schweiz: Leiterlispiel) bezeichnet eine Familie von Brettspielen, die dem traditionellen indischen Spiel Moksha Patamu nachempfunden wurden. Hatte Moksha Patamu noch eine religiöse Bedeutung, so ist diese in den westlichen Versionen gänzlich verschwunden.^[1] Heute ist es in zahlreichen Varianten vor allem als Kinderspiel verbreitet.

Spielprinzip

Ein Leiterspiel-Spielplan enthält eine Kette von Spielfeldern, die von einem Start- zu einem Zielfeld führt und sich spiralförmig oder im Zickzack windet. An mehreren Stellen sind zwei nicht direkt aufeinanderfolgende Felder durch Schlangen, Leitern oder andere Zeichnungen verbunden.

Jeder Spieler beginnt mit einer Spielfigur auf dem Startfeld. Üblicherweise wird reihum ein einzelner Würfel geworfen. Dessen Ergebnis gibt an, wieviele Felder sich die Spielfigur vorwärtsbewegen darf. Endet ihr Zug auf dem Anfangsfeld einer Leiter, wird sie auf deren Endfeld vorgesetzt. Endet er auf einer Schlange, wird sie auf deren Endfeld versetzt, das wieder näher am Anfangsfeld liegt. Sieger ist, wer zuerst das Zielfeld erreicht.

Im Detail gibt es verschiedene Regeln zum punktgenauen Erreichen des Zielfeldes oder der Situation, dass das Endfeld einer Bewegung bereits von einer anderen Figur besetzt ist.

Varianten

Das Spiel ist in seiner Grundform ein reines Glücksspiel ohne strategische Elemente, weshalb es vor allem von und mit jüngeren Kindern gespielt wird. In der englischsprachigen Welt sind die ursprünglichen Leitern und Schlangen als Bilder auf dem Brett weit verbreitet geblieben, was vermutlich auf den immer noch gebräuchlichen Namen Snakes and Ladders zurückgeht. Im deutschen Sprachraum gibt es dagegen seltener Schlangen, sondern eher Alternativen wie Rutschen. Es gibt zahllose Varianten des Spielplanes mit unterschiedlicher Bahnlänge, Abkürzungszahl und -positionierung und zeichnerischer Gestaltung, oft mit bunten Hintergründen und thematisch angepassten Abkürzungen.

Das Grundprinzip des Spiels wird auch oft abgewandelt, indem etwa jeder Spieler mehrere Spielfiguren erhält oder einzelnen Feldern Spezialereignisse zugewiesen werden (rücke 3 Felder vor, setze eine Runde aus...). Das Leiterspiel ist auch eine beliebte Grundlage für Lernspiele, die einen thematischen Hintergrund setzen oder Wissensfragen einbauen.

Geschichte

1893 patentiertes Spielbrett

Das erste westliche Leiterspiel wurde 1892 von der Spielzeugfirma von Frederick Henry Ayres in England mit einem kreisförmigen Spielbrett auf den Markt gebracht. Im Uhrzeigersinn mussten die Spielfiguren bis in die Mitte gezogen werden. Das Spiel hatte insgesamt 100 Felder, auf denen fünf Schlangen und fünf Leitern eingezeichnet waren.^[1]

R. H. Harte entwickelte 1893 eine Variante auf einem rechteckigen Spielfeld. Aus dem gleichen Jahr stammt ein Patent eines ähnlichen rechteckigen Spielbrettes, das nur noch 34 Einzelfelder beinhaltete.^[2]

Um 1920 erschien bei Spear & Söhne ein Spiel mit dem Namen „Auf und Ab! Lustiges Leiterspiel“. Auf dem Brett befanden sich hier keine Schlangen mehr, sondern Zirkusszenen mit derselben Funktion.^[1]

Mathematische Behandlung

Das Leiterspiel lässt sich mathematisch vollständig als Markow-Kette formulieren und dadurch lässt sich ein Erwartungswert für die Spieldauer berechnen. Von jedem Feld aus ergibt sich eine vom Spielwürfel abhängige Wahrscheinlichkeit, welches das nächste Feld der Spielfigur sein wird. Da nur eine Spielfigur pro Spieler auf dem Brett ist, kommt es nicht auf die Entscheidung des Spielers, sondern nur auf die Augenzahl des Würfels an. Da die Figur durch die Schlangen zurückfallen kann, gibt es auch die Möglichkeit, dass eine Spielfigur praktisch ewig auf dem Spielbrett verbleibt. Durch das Gesetz der großen Zahlen kommt aber jede Spielfigur nach unendlich vielen Spielzügen sicher im Zielfeld an. Man kann nun die Wahrscheinlichkeiten ermitteln, die eine Spielfigur auf jedem einzelnen Feld hat, um ein nächstes Feld zu erreichen und wie groß wiederum die Wahrscheinlichkeiten von dort aus sind. Dadurch lässt sich die Kette bis zum letzten Feld erweitern und man hat so vom Start- bis zum Zielfeld eine komplette Wahrscheinlichkeitskette durchgerechnet. Durch diese Berechnung lässt sich nun ein durchschnittlicher Wert für die Anzahl der Spielzüge angeben, bis eine Spielfigur im Ziel ankommt. Die ermittelte durchschnittliche Zugzahl lässt sich zusätzlich mit der Monte-Carlo-Methode verifizieren.

Einzelnachweise

1. ↑ ^{a b c} Erwin Glonnegger, Das Spiele-Buch, Ravensburger Buchverlag, Ravensburg 1988, ISBN 3-473-42601-6
2. ↑ David Parlett, The Oxford History of Board Games, Oxford & New York, 1999, ISBN 0-19-212998-8