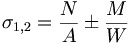- Spannungstrapezverfahren
-
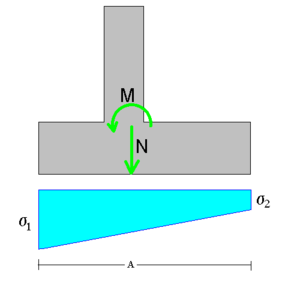
Das Kragträgerverfahren oder Spannungstrapezverfahren ist eine Berechnungsmethode der Statik (speziell der Baustatik). Es ist eine einfache und alte (klassische) zweidimensionale Methode zur Berechnung der Standsicherheit eines Fundaments, einer Stützwand, einer Staumauer oder etwas Vergleichbarem. Alle diese werden auf einen einfachen Balken zurückgeführt, der nur auf einer Seite eingespannt ist, nämlich unten. Diesen Balken nennt man auch Kragträger. Berechnet werden die Spannungen, die der Kragträger bzw. Balken (oder das ganze Bauwerk) bei der Belastung, der er unterworfen ist, auf seine Einspannung oder Aufstandsfläche ausübt. Der Verlauf der Spannungen wird als linear angenommen. Er nimmt die Form eines Trapezes an (daher der Name Spannungstrapezverfahren).
Die zugrunde liegende Formel für die Berechnung der Spannungen ist:
- σ1,2 = Spannungen auf den beiden Seiten,
- N - Normalkraft
- A - Aufstandsfläche
- M - Biegemoment
- W - Widerstandsmoment
Das Verfahren setzt - im Gegensatz zur Stabstatik - voraus, dass der Balken eine Ausdehnung in seiner Breite hat. Diese kann auch über der Höhe variieren. Außerdem wird vorausgesetzt, dass er sich zwar biegen darf, aber nicht in sich verformt, d. h. dass seine Querschnitte eben bleiben (Ebenbleiben der Querschnitte nach der Bernoulli-Hypothese).
Bei einem Fundament ist beispielsweise nachzuweisen, dass an jeder Stelle der Aufstandsfläche des darüber befindlichen Bauwerks Druckspannungen vorhanden sind. Sonst würde das Bauwerk an einer Seite abheben und umkippen.
In verfeinerten Versionen der Balkentheorie können auch die Hauptnormal- und Hauptschubspannungen sowie deren Verlauf bestimmt werden. In einem zusätzlichen Schritt weist man die Gleitsicherheit, die Kippsicherheit und die Sicherheit gegen Auftrieb nach.
Wenn das Kragträgerverfahren angewandt wird, sagt man in Fachkreisen auch, "es wird nach der Balkentheorie gerechnet".
Wikimedia Foundation.