Biegemoment

Als Biegemoment wird ein Drehmoment bezeichnet, das einen Stab, einen Balken, einen Träger oder eine Welle auf Biegung belastet. Es ist diejenige Schnittgröße, die zu bestimmen und mit der der Biegefall statisch zu berechnen ist.^[1]

Balken mit mittiger Einzel-Last

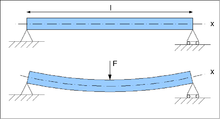
Ein im Querschnitt eines Balkens wirkendes Biegemoment entsteht typischerweise durch eine Kraft (Last), die außerhalb der Auflager quer auf ihn wirkt. Rechnerisch ist es das Produkt aus Kraft und Hebelarmlänge. Im abgebildeten Beispiel hat es seinen maximalen Wert an der Stelle, wo die Kraft F einwirkt, und ist das Produkt aus der sich durch die mittige Lage ergebenden Auflagekraft F / 2 und der sich ergebenden Hebelarmlänge l / 2 :

$M_y(x=l/2) = F/2 \cdot l/2 = Fl/4$ .

Der Index y zeigt an, dass die Biegung um die y -Achse (im Beispiel senkrecht auf der Bildebene) erfolgt.
Die Variable x ist die Koordinate in Längsrichtung des Balkens (x = 0 über einem der beiden Auflager).

Biegelinie

Die Form eines elastisch verbogenen schlanken (dünn relativ zur Länge) Bauteiles mit konstantem Querschnitt - seine Biegelinie w(x) - kann mit folgender Näherungs-Formel beschrieben werden:

$w''(x) = -{M_y(x) \over E I_y}$     (w'' ist die Krümmung der Biegelinie, die in der xz -Ebene (Bildebene) liegt) .

Der Elastizitätsmodul E ist eine Materialeigenschaft, I_y ist das axiale Flächenträgheitsmoment (eine rein geometrische Größe) des Balken-Querschnitts, von dem sein Verhalten bei Biegung um die y -Achse abhängt.

Im Beispiel ist das Biegemoment M_y in Balkenmitte (x=l/2) und damit auch die Krümmung w" der Biegelinie am größten:

$w'' = -{F\cdot l \over 4\cdot E I_y}$

Biegespannung und Festigkeit

Im Beispiel tritt in Balkenmitte nicht nur die maximale Krümmung (w'') der Biegelinie sondern auch die maximale Biegespannung σ_B auf:

$\sigma_B(z) = \frac{M_y(x=l/2)}{I_y} z$ .

Die Höhe der Biegespannung spielt eine Rolle, wenn zu untersuchen ist, ob der Balken die Beanspruchung aushält, sich nicht bleibend verformt oder gar bricht. Sie ist proportional zur Entfernung z von der neutralen Faser (in der Regel durch den Schwerpunkt des Querschnitts gehend). Beim maximalen z_r, das heißt in der oberen Randfaser (Bogeninnenseite) entsteht die größte Druck-Spannung, in der untersten Randfaser (Bogenaußenseite) die größte Zug-Spannung.

Weil bei konstantem Balkenquerschnitt das Flächenträgheitsmoment konstant ist, lässt sich sein Quotient mit dem Abstand der Randfaser z_r zum konstanten Widerstandsmoment

W_y = I_y / z_r

zusammen fassen. Für die in der Randfaser auftretende Biegespannung σ_r gilt damit die Formel:

$\sigma_r(x) = \frac{M_y(x)}{W_y}$ .

Im Beispiel (x=l/2: M_y= Fl/4) hat die die Dimensionierung des Balkens gegen Biege-Versagen bestimmende Spannung den Wert:

$\sigma_r = \frac{F\cdot l}{4\cdot W_y}$

Einzelnachweise

1. ↑ Holzmann / Meyer /Schumpich: Technische Mechanik / Statik, Vieweg+Teubner; Auflage 12., September 2009, ISBN 3834808253

Siehe auch

• Balkentheorie