Spieker-Punkt

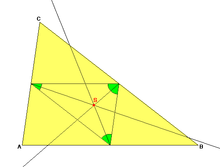
Als Spieker-Punkt oder Spieker-Zentrum eines Dreiecks bezeichnet man den Inkreismittelpunkt des zugehörigen Innendreiecks. Man findet den Spieker-Punkt also dadurch, dass man die Mittelpunkte der Seiten des gegebenen Dreiecks miteinander verbindet und die Winkelhalbierenden des entstandenen neuen Dreiecks (des Innendreiecks) zum Schnitt bringt. Der Spieker-Punkt ist benannt nach dem Gymnasiallehrer Theodor Spieker (1823-1913).^[1]

Der Spieker-Punkt ist rot und mit S markiert

Eigenschaften

• Der Spieker-Punkt eines Dreiecks stimmt mit dem Schwerpunkt des zugehörigen Dreiecksumfangs überein, d.h. also beispielsweise dem Schwerpunkt eines Drahtmodells des Dreiecks.
• Der Spieker-Punkt liegt mit dem Inkreismittelpunkt, dem Schwerpunkt und dem Nagel-Punkt auf einer Geraden. Er halbiert die Verbindungsstrecke zwischen dem Inkreismittelpunkt und dem Nagel-Punkt.
• Der Spieker-Punkt ist Mittelpunkt eines Kreises, der die drei Ankreise rechtwinklig schneidet.
• Der Spieker-Punkt liegt auf der Kiepert-Hyperbel.

Koordinaten

Spieker-Punkt (Spieker-Zentrum, X10)
Trilineare Koordinaten	$bc(b+c) \, : \, ca(c+a) \, : \, ab(a+b)$
Baryzentrische Koordinaten	$(b+c) \, : \, (c+a) \, : \, (a+b)$

WebLinks

• Eric W. Weisstein: Spieker Center. In: MathWorld. (englisch)
• Spiekerpunkt - eine Visualisierung mit GeoGebra, Spiekerpunkt, Inkreis und Schwerpunkt liegen auf einer Geraden
• Spiekerpunkt und Ankreise - eine Visualisierung mit GeoGebra, der Spiekerpunkt ist der Mittelpunkt eines Kreises, der die Ankreise des Dreiecks orthogonal (rechtwinklig) schneidet.

Einzelnachweise

1. ↑ Jürgen Flachsmeyer; Rudolf Fritsch; Hans-Christian Reichel (Hg.) MATHEMATIK-INTERDISZIPLINÄR