Standardisierung (Statistik)

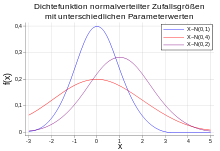Dichten einer standardisierten (blau) und zweier nicht standardisierter Normalverteilungen (rot und violett)

Unter Standardisierung oder z-Transformation versteht man in der mathematischen Statistik eine Transformation einer Zufallsvariablen, so dass die resultierende Zufallsvariable den Erwartungswert Null und die Varianz Eins besitzt. Die Standardabweichung entspricht der Wurzel der Varianz und ist somit auch gleich Eins.

Standardisierung ist z. B. notwendig um unterschiedlich verteilte Zufallsvariablen miteinander vergleichen zu können. Außerdem sind für einige statistische Verfahren, wie beispielsweise der Faktorenanalyse, standardisierte Zufallsvariablen notwendig.

Ist X eine Zufallsvariable mit Erwartungswert $\scriptstyle \operatorname{E}(X) = \mu$ und Varianz $\scriptstyle \operatorname{Var}(X) = \sigma^2$ (und dementsprechend Standardabweichung σ) so erhält man die zugehörige standardisierte Zufallsvariable durch:

$Z=\frac{X-\mu}{\sigma}.$

Für diese so erhaltene Zufallsvariable Z gilt dann:

• $\operatorname{E}(Z)= \operatorname{E}\left(\frac{X-\mu}{\sigma}\right)=\frac{1}{\sigma} \left( \operatorname{E}(X) - \mu\right) = 0$
• $\operatorname{Var}(Z)= \operatorname{Var}\left(\frac{X-\mu}{\sigma}\right)=\operatorname{Var}\left(\frac{X}{\sigma}\right) =\frac{1}{\sigma^2} \operatorname{Var}(X) = 1$

In vielen Statistikprogrammen wie SPSS und Statistica ist die Möglichkeit einer Standardisierung der Messergebnisse bereits eingebaut. Genau genommen sollte hier aber von einer Studentisierung gesprochen werden, da die genaue Verteilung der zugrundeliegenden Zufallsvariablen nicht bekannt ist und somit statt des Erwartungswerts das arithmetische Mittel und statt der Varianz die Stichprobenvarianz verwendet werden muss. Oftmals werden allerdings die Begriffe des Studentisierens und des Standardisierens synonym verwendet.

Der Begriff des z-Transformierens beziehungsweise die Verwendung des Buchstaben Z ist insofern gebräuchlich, als insbesondere im zentralen Grenzwertsatz (dieser beginnt mit einem Z) standardisierte Zufallsvariablen verwendet werden.

Quellen

• Bortz, Schuster Statistik für Human- und Sozialwissenschaftler, 7. Auflage, 2010, Springer
• Falk et al., Foundations of statistical analyses and applications with SAS, 2002, Birkhäuser