- Stichprobenvarianz
-
Die Stichprobenvarianz oder empirische Varianz ist ein Maß für die Streuung von Daten in der (deskriptiven) Statistik. Die Stichprobenstandardabweichung oder empirische Standardabweichung ist die Wurzel aus der Stichprobenvarianz und hat die gleiche Maßeinheit wie die Beobachtungsdaten.
Inhaltsverzeichnis
Berechnung der Stichprobenvarianz
In der Literatur werden zur Berechnung der Stichprobenvarianz verschiedene Formeln verwendet, die korrigierte Stichprobenvarianz
oder die unkorrigierten Stichprobenvarianzen
 oder
oder
mit
 die Beobachtungswerte und
die Beobachtungswerte und  das arithmetisches Mittel der Beobachtungswerte bzw. μ der wahre Mittelwert in der Grundgesamtheit. Welche der Berechnungsformeln benutzt werden kann, hängt von den Eigenschaften der Stichprobe ab.
das arithmetisches Mittel der Beobachtungswerte bzw. μ der wahre Mittelwert in der Grundgesamtheit. Welche der Berechnungsformeln benutzt werden kann, hängt von den Eigenschaften der Stichprobe ab.Stichprobe ist Mittelwert μ der
Grundgesamtheit istFormel für Stichprobenvarianz eine (einfache) Zufallsstichprobe unbekannt s2 bekannt 
eine Vollerhebung s'2 oder 
keine (einfache) Zufallsstichprobe s'2 oder s2 Stichprobe ist eine Zufallsstichprobe
Ist eine Stichprobe eine (einfache) Zufallsstichprobe dann ist das Ziel der Datenanalyse meist ein Rückschluss von der Stichprobe auf die Grundgesamtheit. In den Verfahren der induktiven Statistik für den Rückschluss (Statistische Tests, Konfidenzintervalle etc.) fließt oft die Varianz σ2 der Grundgesamtheit ein.
In der Praxis ist die Varianz der Grundgesamtheit jedoch unbekannt, so dass sie aus den Beobachtungsdaten geschätzt werden muss. Für die Schätzfunktionen
-


(falls μ ebenfalls geschätzt werden muss) 

(falls μ nicht geschätzt werden muss)
kann man zeigen, dass diese Schätzfunktionen erwartungstreu sind für die unbekannte Varianz σ2 der Grundgesamtheit:
 .
.Unter anderem deswegen wird im Rahmen der induktiven Statistik immer s2, falls μ geschätzt werden muss, bzw.
 , falls μ bekannt ist, genutzt.
, falls μ bekannt ist, genutzt.Stichprobe ist eine Vollerhebung
In diesem Fall enthält die Stichprobe alle Elemente der Grundgesamtheit, und s'2 und
 fallen zusammen. Der wahre Mittelwert der Grundgesamtheit μ berechnet sich aus allen Elementen der Grundgesamtheit als
fallen zusammen. Der wahre Mittelwert der Grundgesamtheit μ berechnet sich aus allen Elementen der Grundgesamtheit alsmit N die Anzahl der Elemente der Grundgesamtheit und n die Anzahl der Elemente in der Stichprobe. Bei einer Vollerhebung gelten natürlich N = n und damit
 . Die Varianz der Grundgesamtheit lässt sich dann als mittlere quadratische Abweichung vom Mittelwert berechnen
. Die Varianz der Grundgesamtheit lässt sich dann als mittlere quadratische Abweichung vom Mittelwert berechnen .
.
Stichprobe ist keine Zufallsstichprobe
Ist die Stichprobe keine Zufallsstichprobe, so ist es meist nicht möglich, auf einfache Weise die Varianz der Grundgesamtheit aus den Beobachtungsdaten zu schätzen. Daher dient die Stichprobenvarianz dann nur zur Beschreibung der Streuung der Daten im Sinne der mittleren quadratischen Abweichung vom Mittelwert. Daher sollte die Formel
genutzt werden zwecks eindeutiger Interpretation. Auf der anderen Seite wird im Fall Stichprobe ist eine Zufallsstichprobe die korrigierte Stichprobenvarianz eingesetzt
 ,
,
und bei der Nutzung dieser Formel wird die Stichprobenvarianz im Rahmen der deskriptiven und der induktiven Statistik auf gleiche Weise berechnet. Jedoch ist die Stichprobenvarianz hier nur noch approximativ die mittlere quadratische Abweichung vom Mittelwert.
Entschärft wird das Problem dadurch, dass der Unterschied zwischen s'2 und s2 bei großen Stichprobenumfängen nur klein ist. D.h. nur bei kleinen Stichprobenumfängen muss der Nutzer entscheiden, welche Formel er bevorzugt.
Beispiel
Als Beispiel werden aus einer Standardnormalverteilung n = 5 Zufallszahlen berechnet und es ergeben sich z.B. folgende Beobachtungswerte:
-
i 1 2 3 4 5 xi -0,8223 -0,2789 -0,2537 1,1041 1,5785
mit dem Mittelwert
 . Da die Daten aus einer Standardnormalverteilung stammen, kennt man den wahren Mittelwert von
. Da die Daten aus einer Standardnormalverteilung stammen, kennt man den wahren Mittelwert von  . Und damit ergibt sich
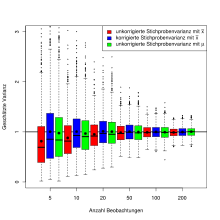
. Und damit ergibt sichDie Grafik rechts zeigt für verschiedene Stichprobenumfänge die geschätzten Varianzen für jeweils 1000 Stichproben mit standardnormalverteilten Daten. Die Farben stehen für verschiedene Schätzer:
 in Rot,
in Rot,  in Blau und
in Blau und  in Grün. Der schwarze Punkt im Boxplot ist der Mittelwert aus den 1000 Schätzungen. Man sieht deutlich, dass für weniger als 50–100 Beobachtungen in der Stichprobe s'2 (Rot) die wahre Varianz von σ2 = 1 unterschätzt wird.
in Grün. Der schwarze Punkt im Boxplot ist der Mittelwert aus den 1000 Schätzungen. Man sieht deutlich, dass für weniger als 50–100 Beobachtungen in der Stichprobe s'2 (Rot) die wahre Varianz von σ2 = 1 unterschätzt wird.
Wikimedia Foundation.