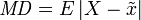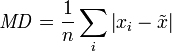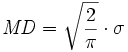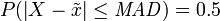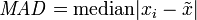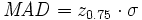Streuungsparameter

Unter Streuung fasst man in der deskriptiven Statistik verschiedene Maßzahlen zusammen zur Beschreibung der Streubreite von Werten einer Häufigkeitsverteilung um ihren Mittelwert. Die verschiedenen Berechnungsmethoden unterscheiden sich prinzipiell durch ihre Beeinflussbarkeit bzw. Empfindlichkeit gegenüber Ausreißern. Die Streuung der Häufigkeitsverteilung wird als Standardfehler bezeichnet.

Maßzahlen

Spannweite (engl.: range)

Die Spannweite ist das einfachste Streuungsmaß und berechnet sich einfach als Distanz zwischen dem größten und dem kleinsten Messwert:

• R = x_max − x_min

R ist aufgrund der Tatsache, dass, unabhängig von der Stichprobengröße, nur zwei Werte (die so genannten Extremwerte) berücksichtigt werden, nicht robust gegenüber Ausreißern.

Siehe auch gleitende Spannweite (engl. moving range).

(Inter-)Quartilabstand (engl.: interquartile range)

Hat man die Quartile Q_.25 und Q_.75 berechnet, so bezeichnet man deren Differenz als Interquartilabstand oder IQR:

• IQR = Q_.75 − Q_.25

Innerhalb des IQR liegen 50% aller Messwerte. Er ist – wie auch der Median bzw. Q_.50 – unempfindlich gegenüber Ausreißern. Es lässt sich zeigen, dass er einen Bruchpunkt von ε ^* = 0.25 hat.

Mittlere Abweichung (engl.: mean deviation from the median, MD)

Die mittlere Abweichung MD vom Median 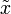$\tilde{x}$ ist definiert durch

• $\mathit{MD} = E\left|X - \tilde{x}\right|$

Im Falle einer konkreten Stichprobe wird sie errechnet durch

• $\mathit{MD} = \frac{1}{n}\sum_i \left|x_i - \tilde{x}\right|$

Durch die Definition ergibt sich im Falle von normalverteilten Daten folgender Zusammenhang zur Standardabweichung:

• $\mathit{MD} = \sqrt{\frac{2}{\pi}} \cdot \sigma$

Mittlere absolute Abweichung (engl.: median absolute deviation, auch: MedMed)

Die mittlere absolute Abweichung MAD ist definiert durch

• $P(\left|X - \tilde{x}\right| \leq \mathit{MAD}) = 0.5$

Im Falle einer konkreten Stichprobe wird sie errechnet durch

• $\mathit{MAD} = \mathrm{median}{\left|x_i - \tilde{x}\right|}$

Durch die Definition ergibt sich im Falle von normalverteilten Daten folgender Zusammenhang zur Standardabweichung:

• $\mathit{MAD} = z_{0.75} \cdot \sigma$

z_0.75 ist das 0.75-Quantil der Standardnormalverteilung und beträgt ca. 0,6745.

Die mittlere absolute Abweichung ist ein robuster Schätzer für die Standardabweichung. Es lässt sich zeigen, dass sie einen Bruchpunkt von 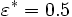$\varepsilon^*=0.5$ hat.

Varianz und Standardabweichung (engl.: variance bzw. standard deviation)

Dies sind die wichtigsten und am meisten verwendeten Streuungsmaße. Siehe separate Artikel zu Varianz, Standardabweichung.

Graphische Darstellungsformen

• Box-Whisker-Plot
• Streudiagramm

Siehe auch

• Moment (Stochastik)
• Homoskedastizität