- Strukturfaktor
-
Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.
Der Strukturfaktor ist ein Maß für das Streuvermögen einer Kristallbasis. Der Strukturfaktor Fhkl gibt die relative Intensität des durch die Millerschen Indizes h, k, l bestimmten Beugungsreflexes an.
- Röntgenbeugung: Die Streuung der elektromagnetischen Strahlung erfolgt an den Elektronen der Atome. Der Strukturfaktor ist die Fouriertransformierte der Elektronenverteilung innerhalb einer Elementarzelle.
- Elektronenbeugung: Die Elektronen werden durch Coulomb-Wechselwirkung an den Hüllenelektronen und den Atomkernen gestreut. Der Strukturfaktor ist die Fouriertransformierte der Ladungsverteilung innerhalb einer Elementarzelle.
- Neutronenbeugung: Neutronen wechselwirken durch starke Wechselwirkung mit den Atomkernen und wegen ihrem magnetischen Moment mit dem magnetischen Moment der Atome. Der Strukturfaktor ist die Fouriertransformierte der Kernverteilung (Nukleonenverteilung) und der magnetischen Struktur innerhalb einer Elementarzelle.
Die Bragg- bzw. äquivalent die Laue-Bedingung gehen vom reinen Kristallgitter (am Gitterpunkt ein punktförmiges Streuzentrum) aus und geben an, in welcher Richtung Beugungsreflexe beobachtet werden können. Die relative Intensität der Reflexe hängt vom Aufbau der Basis, dem Streuvermögen der Basisatome und von der thermischen Bewegung der Atome ab, dies wird durch den Strukturfaktor beschrieben.
Inhaltsverzeichnis
Beschreibung
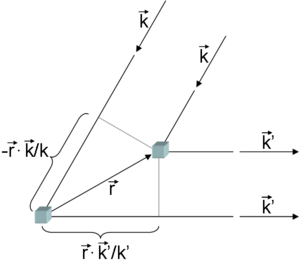
Man wählt einen Referenzpunkt innerhalb der Elementarzelle als Ursprung. Betrachtet werden zwei infinitesimale Volumenelemente dV als Streuzentren, eines am Referenzpunkt
 , eines bei
, eines bei  . Der Wellenvektor der einfallenden Strahlung sei
. Der Wellenvektor der einfallenden Strahlung sei  , der der gestreuten sei
, der der gestreuten sei  . Damit ergibt sich folgender Gangunterschied (Wegdifferenz):
. Damit ergibt sich folgender Gangunterschied (Wegdifferenz):Der Phasenunterschied beträgt (die Streuung sei elastisch, also k = k'):
Nach der Laue-Bedingung können Beugungsreflexe nur beobachtet werden, wenn die Änderung des Wellenvektors beim Streuprozess einem reziproken Gittervektor
 entspricht:
entspricht:  . Dies ergibt eingesetzt:
. Dies ergibt eingesetzt:Nun integriert man über das Volumen einer Elementarzelle VEZ und gewichtet die Phasenunterschiede
![\exp\left[i\,\varphi(\vec{r}\,)\right]](4/2445190bdbdef15f4e59e286694aef2c.png) mit dem Streuvermögen jedes Volumenelements
mit dem Streuvermögen jedes Volumenelements  . Das Streuvermögen ist je nach Beugungsexperiment (siehe oben) die Elektronendichte, die Ladungsdichte oder die Kerndichte.
. Das Streuvermögen ist je nach Beugungsexperiment (siehe oben) die Elektronendichte, die Ladungsdichte oder die Kerndichte.Die am Kristall gebeugte Welle hat eine Amplitude, die proportional zu eben berechneten Größe ist.
Fhkl bezeichnet man als Strukturfaktor. Dieser ist von den Millerschen Indizes h, k, l abhängig, da der reziproke Gittervektor gleich
 ist. Der Strukturfaktor ist somit die Fouriertransformierte des Streuvermögens (z.B. der Elektronendichte)
ist. Der Strukturfaktor ist somit die Fouriertransformierte des Streuvermögens (z.B. der Elektronendichte)  .
.Der Vektor
 lässt sich als Linearkombination der primitiven Gittervektoren
lässt sich als Linearkombination der primitiven Gittervektoren  schreiben:
schreiben:  . Mit der Relation
. Mit der Relation  lässt sich das Skalarprodukt im Exponenten auswerten (VEZ entspricht
lässt sich das Skalarprodukt im Exponenten auswerten (VEZ entspricht ![u_{i}\in [0;1]](4/53400aefa682dc6200b8d23b554acdcc.png) ):
):Der Strukturfaktor ist eine komplexe Größe F = ρeiγ. Als Ergebnis eines Beugungsexperiments beobachtet man die Intensität der gebeugten Welle, die proportional zum Betragsquadrat des Strukturfaktors ist:
Somit gehen alle Phaseninformationen γ verloren. Würde Fhkl als Ergebnis einer Messung zur Verfügung stehen, könnte man durch Fouriertransformation die gesuchte Größe
 finden:
finden:Da aber nur | Fhkl | 2 bekannt ist müssen Näherungsmethoden, wie die Patterson-Methode, verwendet werden um das Phasenproblem zu lösen.
Atomarer Streufaktor
Der Ortsvektor
 wird nun zerlegt in einen Anteil
wird nun zerlegt in einen Anteil  , der vom Bezugspunkt zum Kern des i-ten Atom zeigt, und einen Vektor
, der vom Bezugspunkt zum Kern des i-ten Atom zeigt, und einen Vektor  , der vom Kern des i-ten Atoms zum betrachteten Volumenelement zeigt.
, der vom Kern des i-ten Atoms zum betrachteten Volumenelement zeigt.In der Gleichung für den Strukturfaktor wird das Integral über die ganze Elementarzelle aufgespalten in eine Summe über kleinere Integrationsgebiete, nämlich die Volumina der einzelnen Atome
 . Dabei ist
. Dabei ist  das Streuvermögen (z.B. Elektronendichte) des i-ten Atoms. Die Summe läuft über alle Atome der Basis:
das Streuvermögen (z.B. Elektronendichte) des i-ten Atoms. Die Summe läuft über alle Atome der Basis:Das Integral wird atomarer Streufaktor (oder auch Atomformfaktor)
 des i-ten Atoms genannt:
des i-ten Atoms genannt:Damit schreibt sich der Strukturfaktor wie folgt:
Mit oben eingeführter Komponentenschreibweise:
Betrachtet man zusätzlich noch die thermische Bewegung der Atome, so ist
 zeitabhängig. Nun zerlegt man
zeitabhängig. Nun zerlegt man  in einen mittleren Aufenthaltsort
in einen mittleren Aufenthaltsort  (Gleichgewichtslage, ruhend) und der Auslenkung
(Gleichgewichtslage, ruhend) und der Auslenkung  (zeitabhängig). Letztere führt auf den Debye-Waller-Faktor.
(zeitabhängig). Letztere führt auf den Debye-Waller-Faktor.Beispiel
Als Beispiel wird der Strukturfaktor für eine Cäsiumchloridstruktur berechnet. Das Gitter ist also kubisch primitiv, die primitiven Gittervektoren sind
 ,
,  ,
, . Das eine Basisatom sitzt bei
. Das eine Basisatom sitzt bei  das andere bei
das andere bei  .
.Ist die Summe der Millerschen Indizes gerade, hat der gebeugte Röntgenstrahl eine hohe Intensität, bei ungerader Summe, ist die Intensität minimal. Haben beide Basisatome denselben atomaren Streufaktor f1 = f2 = :f, so ist bei ungerader Summe die Intensität gleich Null; man spricht von vollständiger Auslöschung. Dies trifft beim kubisch-raumzentrierten Gitter (bcc-Gitter) zu, wenn man es im System des kubisch primitiven Gitters mit zwei gleichen Basisatomen beschreibt:
Literatur
- Borchardt-Ott, Walter: Kristallographie: eine Einführung für Naturwissenschaftler. Springer Verlag.
- Massa, Werner: Kristallstrukturbestimmung. Teubner Verlag.
Wikimedia Foundation.




![\int_{V_{EZ}}n(\vec{r}\,)\,\exp\left[i\,\varphi(\vec{r}\,)\right]\mathrm{d}^{3}r=\int_{V_{EZ}}n(\vec{r}\,)\,\exp\left[i\,\vec{G}\cdot\vec{r}\right]\mathrm{d}^{3}r](2/9a278a7adf1b5d6c7df60fb3f9e3b491.png)
![F_{hkl}=\int_{V_{EZ}}n(\vec{r}\,)\,\exp\left[i\,\vec{G}\cdot\vec{r}\right]\mathrm{d}^{3}r](2/222f3c0dceb7f4057d81ccd4e2331684.png)
![F_{hkl}=\int^{1}_{0}\int^{1}_{0}\int^{1}_{0} n(u_{1},u_{2},u_{3})\,\exp\left[2\pi i\left(u_{1}h+u_{2}k+u_{3}l\right)\right]\mathrm{d}u_{1}\mathrm{d}u_{2}\mathrm{d}u_{3}](0/890804acedb7f0be9d4bce7c645670d6.png)

![n(\vec{r}\,)=n(u_{1},u_{2},u_{3})=\sum_{h,k,l=-\infty}^{\infty}F_{hkl}\,\exp\left[-2\pi i\left(u_{1}h+u_{2}k+u_{3}l\right)\right]](6/f36813b6b2ce30d762df4a2900c6bb0c.png)

![F_{hkl}=\sum_{i}\int_{V_{A_{i}}}n_{i}(\vec{\tilde{r}}\,)\,\exp\left[i\,\vec{G}\cdot(\vec{r}_{i}+\vec{\tilde{r}}\,)\right]\mathrm{d}^{3}\tilde{r}=\sum_{i}\exp\left[i\,\vec{G}\cdot\vec{r}_{i}\right]\int_{V_{A_{i}}}n_{i}(\vec{\tilde{r}}\,)\,\exp\left[i\,\vec{G}\cdot\vec{\tilde{r}}\right]\mathrm{d}^{3}\tilde{r}](3/3239b55643305a07fb95fae8b67752a7.png)
![f_{i}=\int_{V_{A_{i}}}n_{i}(\vec{\tilde{r}}\,)\,\exp\left[i\,\vec{G}\cdot\vec{\tilde{r}}\right]\mathrm{d}^{3}\tilde{r}](0/3402d26cd6124192c08717342d52d196.png)
![F_{hkl}=\sum_{i}f_{i}\,\exp\left[i\,\vec{G}\cdot\vec{r}_{i}\right]](a/0cabe3dfff2a3eb3e6fb8a0a508776c0.png)
![F_{hkl}=\sum_{i}f_{i}\,\exp\left[2\pi i\,\left(u_{i,1}h+u_{i,2}k+u_{i,3}l\right)\right]](b/6eb59ebc9086feece90832356ced4a9e.png)
![\begin{align}
F_{hkl} & = \sum_{i=1}^{2}f_{i}\,\exp\left[2\pi i\,\left(u_{i,1}h+u_{i,2}k+u_{i,3}l\right)\right] \\
& = f_{1}\,\exp\left[2\pi i\,\left(0\cdot h+0\cdot k+0\cdot l\right)\right] + f_{2}\,\exp\left[2\pi i\,\left(\frac{1}{2}h+\frac{1}{2}k+\frac{1}{2}l\right)\right] \\
& = f_{1} + f_{2} \,\exp\left[\pi i\,\left(h+k+l\right)\right] \\
& = f_{1} + f_{2} (-1)^{h+k+l} \\
\end{align}](6/d262ba2c032e396d9e15f491687803de.png)

