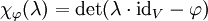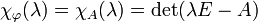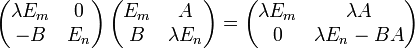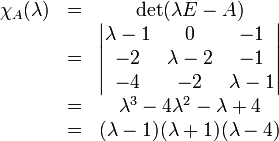- Säkulargleichung
-
Das charakteristische Polynom (Abk.: CP) einer linearen Abbildung, manchmal auch Säkulargleichung genannt, ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Dieses Polynom, das nur für Endomorphismen von endlich dimensionalen Vektorräumen definiert ist, gibt Auskunft über einige Eigenschaften der linearen Abbildung.
Inhaltsverzeichnis
Definition
Sei V ein endlichdimensionaler Vektorraum der Dimension
 und
und 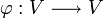 ein Endomorphismus. Dann ist das charakteristische Polynom
ein Endomorphismus. Dann ist das charakteristische Polynom 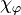 gegeben durch (s. auch Herleitung):
gegeben durch (s. auch Herleitung):Zur Berechnung des charakteristischen Polynoms benötigt man eine Darstellungsmatrix A der linearen Abbildung
 . Dann lässt sich das charakteristische Polynom wie folgt berechnen:
. Dann lässt sich das charakteristische Polynom wie folgt berechnen:Hierbei ist E die n-dimensionale Einheitsmatrix und det steht für die Determinante.
Das charakteristische Polynom ist ein normiertes Polynom n-ten Grades aus K[λ]. Die Notation für das charakteristische Polynom ist sehr uneinheitlich, andere Varianten sind beispielsweise CPA(λ) oder bei Bourbaki PcA(λ).
Die auch gebräuchliche Definition det(A − λE) ist etwas ungeschickter, da dann der Leitkoeffizient bei ungeradem n zu -1 wird und das Polynom dann nicht mehr normiert ist.
Zusammenhang mit Eigenwerten
Das charakteristische Polynom spielt eine wichtige Rolle bei der Bestimmung der Eigenwerte einer Matrix, denn die Eigenwerte sind genau die Nullstellen des charakteristischen Polynoms. Auch wenn man zum expliziten Berechnen des charakteristische Polynoms immer eine Basis und damit eine Darstellungsmatrix auswählt, hängt das Polynom, wie auch die Determinante nicht von dieser Wahl ab.
Um zu zeigen, dass die Eigenwerte gerade die Nullstellen des charakteristischen Polynoms sind, geht man folgendermaßen vor:
Es sei
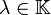 und A eine
und A eine  -Matrix über
-Matrix über 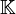 . Dann gelten die folgenden Äquivalenzen:
. Dann gelten die folgenden Äquivalenzen:-
- λ ist ein Eigenwert von A.
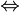 Es gibt ein
Es gibt ein 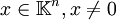 mit Ax = λx.
mit Ax = λx.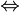 Es gibt ein
Es gibt ein 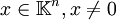 mit (λE − A)x = 0.
mit (λE − A)x = 0.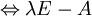 ist nicht invertierbar.
ist nicht invertierbar.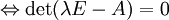
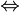 λ ist Nullstelle des charakteristischen Polynoms von A.
λ ist Nullstelle des charakteristischen Polynoms von A.
Formeln
Schreibt man das charakteristische Polynom in der Form
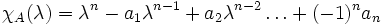 ,
,
so ist stets a1 die Spur und an die Determinante von A.
Speziell für 2 x 2-Matrizen hat das charakteristische Polynom also die besonders einfache Form
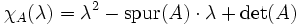 .
.
Für 3 x 3-Matrizen ergibt sich die Form:
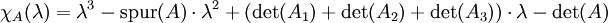 .
.
Hierbei ist Ai die
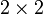 -Matrix, die man durch Streichen der i-ten Zeile und der i-ten Spalte erhält (ein Minor).
-Matrix, die man durch Streichen der i-ten Zeile und der i-ten Spalte erhält (ein Minor).Eigenschaften
- Die charakteristischen Polynome zweier ähnlicher Matrizen sind gleich. Die Umkehrung ist jedoch im Allgemeinen nicht richtig.
- Die Matrix A und ihre Transponierte besitzen das gleiche charakteristische Polynom.
- Nach dem Satz von Cayley-Hamilton ist eine Matrix Nullstelle ihres charakteristischen Polynoms:
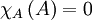 .
.
- Das Minimalpolynom einer linearen Abbildung teilt deren charakteristisches Polynom.
- Ist A eine
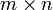 -Matrix und B eine
-Matrix und B eine 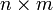 -Matrix so gilt
-Matrix so gilt 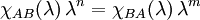 .
.
Beweis:
- Aus den Matrixgleichungen
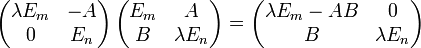
- sowie der Regel
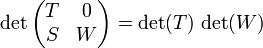
- folgt
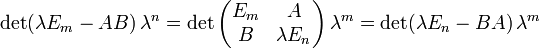 .
.
Beispiel
Gesucht ist das charakteristische Polynom der Matrix
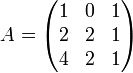 .
.
Gemäß der obigen Definition rechnet man wie folgt:
Damit sind 1, -1 und 4 die Nullstellen des charakteristischen Polynoms χA(λ) und somit auch die Eigenwerte der Matrix A.
Weblinks
Wikimedia Foundation.