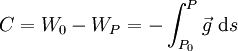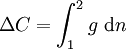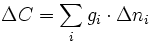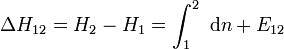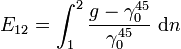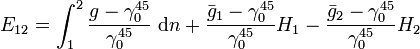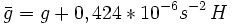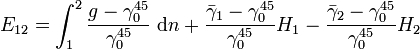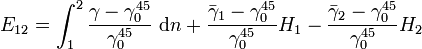Theoretischer Schleifenabschlussfehler

Eine Höhe ist in der höheren Geodäsie die Positionsangabe des lotrechten Abstands von einer Referenzfläche. Man benutzt als Höhenreferenzfläche ein Geoid, Quasigeoid oder auch ein geodynamisch angepasstes Referenzellipsoid. Die Höhe dieser Bezugsflächen wird an einem mittlerem Meeresspiegel (auch Pegel genannt) festgemacht. Je nach Land oder Anwendung werden unterschiedliche Höhendefinitionen und unterschiedliche Pegel verwendet (siehe Höhe über dem Meeresspiegel).

Die wichtigsten Höhendefinitionen: ellipsoidische Höhe h, Normalhöhe H_N und orthometrische Höhe H

Höhendefinitionen

Im Allgemeinen wird erwartet, dass

1. eine Höhe eine geometrische Größe ist und in Längeneinheiten gemessen wird und
2. zwischen Punkten gleicher Höhe kein Wasser fließt.

Dass Höhen nicht gleichzeitig geometrisch (1) und physikalisch (2) korrekt sein können, kann man sich wie folgt verdeutlichen: Zu Punkt (2) müssten die Punkte das gleiche Schwerepotential aufweisen und somit auf einer Äquipotentialfläche der Schwere liegen. Aufgrund der Erdrotation und lokaler Unregelmäßigkeiten im Masseaufbau der Erde verlaufen die Äquipotentialflächen jedoch nicht parallel. So ist die Schwerkraft aufgrund der Erdrotation an den Polen 1/200 größer als am Äquator, die Potentialflächen liegen damit an den Polen um 1/200 enger beisammen.

Es werden daher einige rein geometrisch bzw. physikalisch definierte Höhen verwendet:

1. ellipsoidische Höhen (GPS-Höhen) als rein geometrische definierte Höhen, ausgedrückt in einer Längeneinheit,
2. Geopotentielle Koten als rein physikalische Höhen, die Differenz zweier Schwerepotentiale.

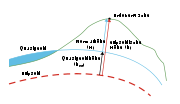
Beim Nivellement erhält man abweichende Höhendifferenzen, wenn man entlang verschiedener Wege nivelliert. Grund für den sogenannten theoretischen Schleifenabschlussfehler ist, dass die Höhenübertragung entlang der nicht parallelen Äquipotentialflächen erfolgt, die Differenzen aber in Meter gemessen werden. Um die Widersprüche zu beseitigen, ist für ausgedehnte Gebiete mit größeren Höhendifferenzen eine Berücksichtigung des Schwerefeldes notwendig. Für die Praxis sind verschiedene metrische Höhensysteme, die die Schwere berücksichtigen, entwickelt worden:

• orthometrische Höhen,
• Normalhöhen,
• normal-orthometrische bzw. normal-sphäroidische Höhen.

Zwischen den Höhensystemen bestehen merkliche Unterschiede, die im Hochgebirge Größenordnungen von Zentimetern bis Dezimetern pro Kilometer erreichen können. Die Unregelmäßigkeiten im Erdschwerefeld werden seit etwa 100 Jahren unter den Begriffen Lotabweichung bzw. Schwereanomalie und Geoid erforscht und heute ausreichend genau messtechnisch erfasst.

Ellipsoidische Höhen

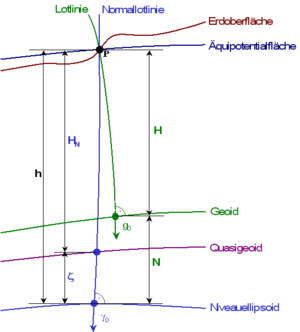
Geometrisch definierte Höhen werden heute als ellipsoidische Höhe h bezeichnet. Diese geben den Abstand eines Punktes von einem geodynamisch definierten Referenzellipsoiden entlang der Ellipsoidnormalen an. Zwei Punkte gleicher ellipsoidischer Höhe liegen jedoch nicht auf derselben Äquipotentialfläche, sodass zwischen ihnen Wasser fließen kann.

Ellipsoidische Höhen können direkt mittels GPS bestimmt werden. Eine einfache Umrechnung von nivellierten in ellipsoidische Höhen ohne Kenntnis der Schwerestörungen ist nicht möglich. Alternativ können ellipsoidische Höhen durch Anlegen eines Raumpolygonzuges bestimmt werden.

Geopotentielle Koten

Eine Geopotentielle Kote C ist die negative Schwerepotentialdifferenz des Punktes zum Geoid. Punkte gleicher geopotentieller Kote liegen somit auf einer Äquipotentialfläche.

$C=W_0-W_P=-\int_{P_0}^{P}\vec g\ \mathrm ds$

Da es sich um eine Schwerepotentialdifferenz handelt ist die SI-Einheit Joule pro Kilogramm (J/kg) bzw. (m²/s²). Zum Teil werden auch geopotential units (gpu) als Einheit verwendet (1 gpu = 10 J/kg). Früher wurden geopotentielle Koten auch in der Einheit geopotentieller Meter (gpm) angegeben. 1 gpm entspricht 9,80665 J/kg. Der Betrag entspricht dem der dynamischen Höhe. Geopotentielle Koten können aus nivellierten Höhenunterschieden Δn und Schweremessungen g bestimmt werden.

$\Delta C=\int_1^2 g \ \mathrm dn$

bzw.

$\Delta C=\sum_i g_i\cdot\Delta n_i$

Dynamische Höhen

Dynamische Höhen H_Dyn werden aus den Geopotentiellen Koten in der Regel mit der Normalschwere auf Meeresniveau bei 45° Breite 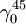$\gamma_0^{45}$ in die Dimension Meter umgerechnet. Sie drücken den Abstand aus, den die Äquipotentialflächen bei 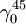$\gamma_0^{45}$ hätten. Der tatsächliche (metrische) Abstand variiert allerdings aufgrund der geringeren Schwerebeschleunigung am Äquator gegenüber den Polen um etwa 5 / 1000.

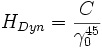$H_{Dyn}=\frac{C}{\gamma_0^{45}}$ mit $\gamma_0^{45}=9{,}80665\, \mathrm {\frac{m}{s^2}}$

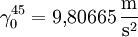
Dynamische Höhen sind wegen der großen dynamischen Korrektionen für die Praxis unbrauchbar. Sie ergeben sich aber direkt durch eine "Umskalierung" der geopotentiellen Kote.

Orthometrische Höhen

Die orthometrische Höhe H resultiert aus dem Abstand entlang der gekrümmten Lotlinie zwischen einem Punkt auf der Erdoberfläche und dem Geoid. Die geopotentiellen Koten werden mit der mittleren Schwerebeschleunigung 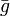$\bar g$ entlang der Lotlinie umgerechnet. Die Schwere kann im Erdinneren nicht gemessen werden, so dass sie nur durch Aufstellen einer Hypothese über die Masseverteilung berechnet werden kann. Orthometrische Höhen sind somit hypothesenbehaftet. Punkte gleicher orthometrischer Höhe liegen in der Regel nicht auf der gleichen Niveaufläche.

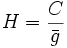$H=\frac{C}{\bar g}$ mit $\bar g=\frac{1}{H} \int_{0}^{H}g\ \mathrm dH$

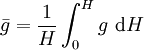
Die Abweichung zwischen der ellipsoidischen und der orthometrischen Höhe wird Geoidundulation N genannt. Sie beträgt global bis zu 100 m, innerhalb der Schweiz z. B. maximal 5 m.

N = h − H

Normalhöhen

Normalhöhe, Quasigeoid und Höhenanormalie

Normalhöhen H_N beschreiben den Abstand eines Punktes entlang der leicht gekrümmten normalen Lotlinie vom Quasigeoid. Für die Umrechnung der geopotentiellen Koten wird die mittlere Normalschwere 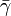$\bar\gamma$ benutzt. Die Normalhöhe ist anders als die orthometrische Höhe hypothesenfrei bestimmbar. Sie wurden von dem sowjetischen Geophysiker Michail Sergejewitsch Molodenski entwickelt.

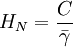$H_{N}=\frac{C}{\bar\gamma}$ mit $\bar\gamma=\frac{1}{H_N}\int_0^{H_N}\gamma\, \mathrm d{H_N}$

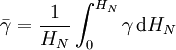
Die Abweichung zwischen der ellipsoidischen Höhe und der Normalhöhe wird Höhenanomalie oder Quasigeoidhöhe ζ genannt. Sie beträgt in Deutschland zwischen 36 und 50 m. Normalhöhen und orthometrische Höhen unterscheiden sich wegen Abweichung der tatsächlichen Schwere von der Normalschwere. Die Unterschiede können im Hochgebirge bis zu einem Meter oder mehr betragen, im Flachland liegen sie oft nur im Millimeterbereich. In den alten Bundesländern betragen sie -5 bis +4 cm.

ζ = h − H_N

Normal-orthometrische Höhen

Liegen keine Schweremessungen vor, kann die Schwerekorrektur der beobachteten Höhenunterschiede nur mit der Normalschwere durchgeführt werden. Die abgeleiteten Höhen nennt man dann normal-orthometrische Höhen oder sphäroidisch-orthometrische Höhen H_Sph. Die Abweichungen zu Normalhöhen fallen gering aus, da sich die Korrekturen nur wegen des kleinen Anteil des Oberflächenfreiluftgradienten unterscheiden.

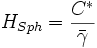$H_{Sph}=\frac{C^{*}}{\bar\gamma}$ mit $C^{*}=\int_0^1\gamma \ \mathrm dn$

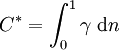
Korrektionen

Die eigentliche Messgröße der Höhenmessung sind keine Höhen über dem Meeresspiegel, sondern Höhenunterschiede ΔH. Diese werden in der Landesvermessung üblicherweise durch Nivellement bestimmt. Um die gemessenen Höhenunterschiede dn in eine der Höhendefinitionen umzurechnen sind Korrektionen E anzubringen.

$\Delta H_{12} = H_2-H_1=\int_1^2\ \mathrm dn+E_{12}$

dynamische Korrektion

Durch dynamische Korrektion lassen sich die nivellierten Höhenunterschiede in dynamische Höhenunterschiede umrechnen.

$E_{12}=\int_1^2\frac{g-\gamma_0^{45}}{\gamma_0^{45}} \ \mathrm dn$

orthometrische Korrektion

Bei der orthometrischen Korrektion kommen zum streng bestimmbaren dynamischen Anteil zwei hypothesenbehaftete ortsabhänge Anteile.

$E_{12}=\int_1^2\frac{g-\gamma_0^{45}}{\gamma_0^{45}}\ \mathrm dn + \frac{\bar g_1-\gamma_0^{45}}{\gamma_0^{45}}H_1 - \frac{\bar g_2-\gamma_0^{45}}{\gamma_0^{45}}H_2$

Unter der Annahme der mittleren Erdkrustendichte von 2,67 g/cm³ gilt für die mittleren Schwere $\bar g$:

$\bar g=g+0,424*10^{-6}s^{-2}\,H$

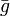normale Korrektion

Analog dazu können mit der normalen Korrektion Normalhöhenunterschiede berechnet werden. Hier werden anstelle der mittleren Schweren 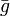$\bar g$ die hypothesefreien mittleren Normalschweren 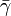$\bar\gamma$ verwendet.

$E_{12}=\int_1^2\frac{g-\gamma_0^{45}}{\gamma_0^{45}} \ \mathrm dn + \frac{\bar\gamma_1-\gamma_0^{45}}{\gamma_0^{45}}H_1 - \frac{\bar\gamma_2-\gamma_0^{45}}{\gamma_0^{45}}H_2$

normal-orthometrische Korrektion

Bei der normal-orthometrischen Korrektion wird anstelle der gemessenen Schwere g die Normalschwere γ zur dynamischen Korrektion benutzt.

$E_{12}=\int_1^2\frac{\gamma-\gamma_0^{45}}{\gamma_0^{45}}\ \mathrm dn + \frac{\bar\gamma_1-\gamma_0^{45}}{\gamma_0^{45}}H_1 - \frac{\bar\gamma_2-\gamma_0^{45}}{\gamma_0^{45}}H_2$

Übersicht

Name	Geopotentielle Kote	Dynamische Höhe	Orthometrische Höhe	Normalhöhe	normal-ortho- metrische Höhe	Nivellierte Höhe	Ellipsoidische Höhe
Kürzel	C	HDyn	H	HN	HSph		h
Einheit	m²/s² = J/kg = 0,1 gpu	m	m	m	m	m	m
Bezugsfläche	Geoid	Geoid	Geoid	Quasigeoid			Referenzellipsoid
Bestimmung	Nivellement	Nivellement	Nivellement	Nivellement	Nivellement	Nivellement	GPS / Raumpolygon
Schweremessungen notwendig	ja	ja	ja	ja	nein	nein	nein
Hypothese für die Dichteverteilung im Erdinneren notwendig	nein	nein	ja	nein	nein	nein	nein
Nivellementschleifen- abschlussfehler	nein	nein	nein	nein auf der Oberfläche	ja (-)	ja (--)
Äquipotentialflächen	alle Höhen	alle Höhen	bei Höhe null	keine (genähert bei Höhe null)	keine (-)	keine (--)	keine (---)

physikalisch (schwerebezogen) ↔ geometrisch

Siehe auch

• Höhe, Höhenmessung

Literatur

• Wolfgang Torge: Geodäsie. 2. Auflage. Walter de Gruyter, Berlin u.a. 2003, ISBN 3-11-017545-2

Weblinks

• Höhenreferenzsysteme. Deutsches Bundesamt für Kartographie und Geodäsie
• Abbildung: Höhen und Bezugsflächen