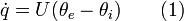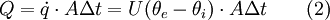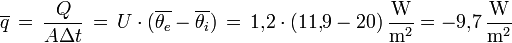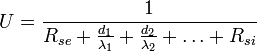Thermische Leitfähigkeit

Der Wärmedurchgangskoeffizient U (auch Wärmedämmwert, U-Wert, früher k-Wert^[1]) ist ein Maß für den Wärmestromdurchgang durch eine ein- oder mehrlagige Materialschicht, wenn auf beiden Seiten verschiedene Temperaturen anliegen. Er gibt die Energiemenge (in Joule=Wattsekunden) an, die in einer Sekunde durch eine Fläche von 1 m² fließt, wenn sich die beidseitig anliegenden Lufttemperaturen stationär um 1 K unterscheiden. Der Wärmedurchgangskoeffizient in W/(K·m²) ist eine spezifische Kennzahl der Materialzusammensetzung eines Bauteils.

Anmerkung: Für die Messung sind stationäre Temperaturen wichtig, damit die Wärmespeicherfähigkeit der Materialien bei Temperaturänderungen das Messergebnis nicht verfälscht. Bei der Betrachtung eines längeren Zeitraums sollten sich auftretende Fehler aber weitestgehend ausgleichen.

Der Kehrwert des Wärmedurchgangskoeffizienten ist der Wärmedurchgangswiderstand R_T in (K·m²)/W.^[1]

• Je höher der Wärmedurchgangskoeffizient, desto schlechter ist die Wärmedämmeigenschaft des Stoffs
• Je höher der Wärmedurchgangswiderstand, desto besser ist die Wärmedämmeigenschaft.

Besonders weit verbreitete Anwendung findet der Wärmedurchgangskoeffizient im Bauwesen, wo er zur Bestimmung der Transmissionswärmeverluste durch Bauteile hindurch dient.

Definition und Bedeutung

Die Wärmestromdichte 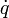$\dot{q}$ (SI-Einheit Watt/Meter²) durch ein Bauteil, das auf der einen Seite der Außenlufttemperatur θ_e und auf der anderen Seite der Innenlufttemperatur θ_i ausgesetzt wird, ist im stationären Zustand proportional zur Temperaturdifferenz θ_e − θ_i, mit der Proportionalitätskonstanten U:

$\dot{q} = U (\theta_{e} - \theta_{i})\qquad (1)$

Die abgeleitete SI-Einheit des U-Wertes ist W/(m²·K) mit den Einheitenzeichen W für die Maßeinheit Watt und K für Kelvin.

Er beschreibt somit die Menge der Wärmeenergie in Joule (=Wattsekunden), die im Zeitraum von einer Sekunde, über eine Fläche von einem Quadratmeter durch eine Trennwand zwischen zwei Räumen durchgelassen wird, wenn sich die beiderseits anliegenden Temperaturen stationär (also nicht nur während der Meßsekunde) um 1 K (= 1 °C) unterscheiden. Die Einheit Wattsekunden der Energie kommt in der endgültigen Einheit des U-Wertes nicht mehr ausdrücklich vor, da sich die Zeitkomponente („-sekunden“) in der Energieeinheit gegen die Zeitkomponente im Nenner („je Sekunde“) wegkürzt. Man könnte die Einheit von U demnach auch als J/(s·m²·K) auffassen.

Der so definierte U-Wert ist daher ein Maß für die „Wärmedurchlässigkeit“ bzw. die Wärmedämmeigenschaften von Bauteilen, also zum Beispiel einer bestimmten Verglasung eines Fensters. Ein Bauteil mit einem kleinen U-Wert lässt dabei weniger Wärme durch als ein Bauteil mit einem größeren U-Wert. Die während der Zeitspanne Δt durch die Fläche A getretene Wärmemenge Q ist

$Q = \dot{q} \cdot A \Delta t = U (\theta_{e} - \theta_{i}) \cdot A \Delta t \qquad (2)$

Betrachtet wird hier die Wärmestromdichte zwischen den beiderseits an einem Bauteil anliegenden Medien (z.B. Innenluft zu Außenluft). Möchte man nicht die Eigenschaften des gesamten Bauteils, sondern die der verwendeten Materialien ermitteln (z.B. Oberflächentemperatur innen zu außen), so ist anstelle des Wärmedurchgangskoeffizienten des Bauteils sein Wärmedurchlasskoeffizient zu benutzen (siehe auch unten).

Einschränkungen der Definition

Die Definitionsgleichung (1) setzt stationäre Verhältnisse voraus und ist nicht geeignet, die jeweils momentane Wärmestromdichte 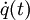$\dot{q}(t)$ bei zeitlich veränderlichen Temperaturen zu berechnen. So treten etwa bei einem Erwärmungsvorgang aufgrund der Wärmespeicherfähigkeit des Bauteils Verzögerungseffekte ein, die beim Versuch, die Oberflächenwärmeströme mittels Gleichung (1) zu berechnen, unberücksichtigt bleiben. Beim darauffolgenden Abkühlvorgang tritt der Fehler jedoch im umgekehrten Sinne auf. Wenn Erwärmen und Abkühlen symmetrisch zueinander erfolgen, heben sich die beiden Fehler auf. 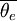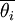Wie sich zeigen lässt ^[2], gilt im Fall streng periodisch verlaufender Temperaturänderungen Gleichung (2) nach wie vor, wenn sie zur Berechnung der während einer Periodendauer Δt verlorenen Wärmemenge Q verwendet wird und die über die Periode gemittelten Temperaturmittelwerte $\overline{\theta_{e}}$ und $\overline{\theta_{i}}$ angesetzt werden:

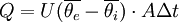$Q = U (\overline{\theta_{e}} - \overline{\theta_{i}}) \cdot A \Delta t$    (für periodische Temperaturänderungen)

Die in der Realität auftretenden Temperaturänderungen sind nie streng periodisch, der dadurch verursachte Fehler hängt jedoch lediglich mit den leicht unterschiedlichen Wärmeinhalten des Bauteils zu Beginn und am Ende der betrachteten Zeitspanne zusammen und bleibt daher begrenzt. Er ist gegenüber dem mit zunehmend längerer Betrachtungsdauer Δt ständig anwachsenden Gesamtwärmeverlust Q schließlich völlig vernachlässigbar ^[3][4], sofern das Gebäude Klimabedingungen ausgesetzt ist, unter denen es im längerfristigen Mittel einen Transmissionswärmeverlust erleidet:

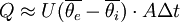$Q \approx U (\overline{\theta_{e}} - \overline{\theta_{i}}) \cdot A \Delta t$    (für beliebige Temperaturänderungen und hinreichend große Δt)

Der U-Wert ist daher trotz seiner zunächst auf stationäre Verhältnisse beschränkten Definition auch unter realen instationären Bedingungen ein geeignetes Maß für die über eine längere Zeitspanne summierten Transmissionswärmeverluste durch den Regelquerschnitt eines Bauteils, welche durch unterschiedliche mittlere Temperaturen der Innen- und Außenluft verursacht werden. Darauf beruht seine Bedeutung als ein wichtiges Kriterium bei der energetischen Bewertung eines Gebäudes.

Vergleich von stationärem und instationärem Verhalten

Vergleich des instationären Wärmestroms mit dem anhand des U-Wertes bestimmten mittleren Wärmestrom

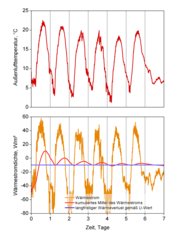
In der nebenstehenden Abbildung sind diese Zusammenhänge an einem konkreten Beispiel illustriert. Betrachtet wird ein 40 cm dickes Vollziegelmauerwerk mit einem U-Wert von 1,2 W/(m²K), das auf der Außenseite den im oberen Bildteil wiedergegebenen Außenlufttemperaturen ausgesetzt ist, während auf der Innenseite konstant eine Temperatur von 20°C anliegt. Bei den Außenlufttemperaturen handelt es sich um reale fünfminütliche Messdaten von sieben Tagen im Mai 2006.

Die orange Kurve im unteren Bildteil zeigt den Wärmestrom durch die Außenoberfläche der Wand, wie er mittels eines instationären Berechnungsprogramms ebenfalls in Fünf-Minuten-Schritten aus den vorliegenden Daten ermittelt wurde (positive Ströme fließen in die Wand hinein, negative Ströme heraus). Die starken Schwankungen des Wärmestroms zeigen den deutlich instationären Charakter der Situation. Der Mittelwert der Außenlufttemperatur während der betrachteten sieben Tage beträgt 11,9°C. Der U-Wert sagt daher einen mittleren Wärmeverlust

$\overline{q} \, = \, \frac{Q}{A \Delta t} \, = \, U \cdot (\overline{\theta_{e}} - \overline{\theta_{i}}) \, = \, 1{,}2 \cdot (11{,}9 - 20) \, \mathrm{\frac{W}{m^2}} = -9{,}7 \, \mathrm{\frac{W}{m^2}}$

voraus. Dieser Wert ist als blaue Linie eingetragen. Die rote Kurve im unteren Bildteil zeigt den kumulierten Mittelwert des Wärmestroms, also nacheinander den Mittelwert über fünf Minuten, über zehn Minuten, über fünfzehn Minuten usw., bis auf der rechten Seite schließlich der Mittelwert über die ganzen sieben Tage erreicht ist. Wie sich deutlich erkennen lässt, mitteln sich mit zunehmendem Mittelungszeitraum die instationären Schwankungen des Wärmestroms rasch weg und nähern sich innerhalb der sieben Tage bereits beinahe perfekt dem vom U-Wert vorhergesagten Mittelwert an.

Das kumulierte Mittel liegt anfangs systematisch über dem U-Wert-Resultat, weil nach vorhergehenden kühleren Tagen (hier nicht dargestellt) das Aufwärmen der Wand zunächst einen überdurchschnittlichen Wärmestrom in die Wand hinein erforderte. Selbst diese Abweichung spielt nach mehreren Tagen Mittelwertbildung keine Rolle mehr.

Der Einfachheit halber wurden Wärmeeinträge durch Sonnenstrahlung hier nicht angesetzt. Sie könnten beispielsweise durch geeignete Erhöhung der Außenlufttemperaturen (zu so genannten Strahlungslufttemperaturen oder kombinierten Außentemperaturen) berücksichtigt werden. An den mathematischen Zusammenhängen und dem generellen Verhalten ändert sich dadurch nichts ^[5].

Berechnung des U-Werts von Bauteilen und Materialien

Die Berechnung des Wärmedurchgangskoeffizienten für den öffentlich-rechtlichen Nachweis im Bauwesen erfolgt nach den Berechnungsschritten gemäß ISO 6946, wo auch kompliziertere baurelevante Fälle behandelt sind. Die erforderlichen Bemessungswerte sind in EN 12524 und DIN 4108-4 festgelegt.

Ideale Wand

Im Falle einer ebenen, unendlich ausgedehnten Wand, welche sich aus hintereinander liegenden Schichten der Dicken d_i und der Wärmeleitfähigkeiten λ_i zusammensetzt, berechnet sich die Proportionalitätskonstante nach:

$U = \frac{1}{R_{se} + \frac{d_1}{\lambda_1} + \frac{d_2}{\lambda_2} + \dots + R_{si}}$

mit

U: Wärmedurchgangskoeffizient in W/(K·m²)

R_se: äußerer Wärmeübergangswiderstand in (K·m²)/W

d₁: Schichtdicke der ersten Schicht in m

λ₁: spezifische Wärmeleitfähigkeit der ersten Schicht in W/(K·m)

d₂: Schichtdicke der zweiten Schicht in m

λ₂: spezifische Wärmeleitfähigkeit der zweiten Schicht in W/(K·m)

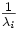$\tfrac{1}{\lambda_i}$: R_λ, der spezifische Wärmewiderstand der i-ten Schicht in (K·m)/W

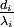$\tfrac{d_i}{\lambda_i}$: R, der Wärmedurchlasswiderstand dieser Schicht in (K·m²)/W

R_si: innerer Wärmeübergangswiderstand in (K·m²)/W

Bauteile

Der Wärmedurchgang eines Bauteils hängt ab von den Wärmeleitfähigkeiten der verwendeten Materialien und deren Schichtdicken sowie von der Bauteilgeometrie (ebene Wand, zylindrisch gekrümmte Rohrwandung, etc.) und den Übergangsbedingungen an den Bauteiloberflächen.

Generell setzt sich der Wärmedurchgangswiderstand aus der Summe der Wärmedurchlasswiderstände der einzelnen hintereinander liegenden Bauteilschichten sowie der Wärmeübergangswiderstände zu den umgebenden Fluiden (Luft, Wasser, etc.) an den beiden Oberflächen zusammen:

Wärmedurchgangswiderstand = Wärmedurchlasswiderstände + Wärmeübergangswiderstände.

Der Wärmedurchgangskoeffizient ist dann das Reziproke des so berechneten Wärmedurchgangswiderstands.

Messung des U-Wertes von Bauteilen und Materialien

Die Ermittlung genauer Wärmedurchlasskoeffizienten ist sehr aufwendig. Die Versuche zur Zertifizierung von Baustoffkennwerten werden von Materialforschungs- und Prüfanstalten im Auftrag der Hersteller an komplexen Prüfeinrichtungen vorgenommen, um vergleichbaren Bedingungen zu garantieren.

U-Wert Messgerät

Mit einem speziellen Temperaturfühler zur U-Wert Bestimmung, einem kompatiblen Messgerät und einem weiteren Temperaturfühler kann der Wärmedurchgangskoeffizient (U-Wert) eines Bauteiles am Einsatzort (z. B. Baustelle) zerstörungsfrei ermittelt werden. Der U-Wert ist ein wichtiger Indikator für die Beurteilung der wärmetechnischen Eigenschaften der Gebäudehülle. Für die Messung des U-Wertes werden ermittelt:

• Oberflächentemperatur T_w des Bauteiles (innen)
• Innentemperatur T_i
• Außentemperatur T_a

Zur Messung der Außentemperatur wird ein Funkfühler verwendet. Alle Daten werden über ein Messprogramm im Messgerät aufgezeichnet, gespeichert und anschließend mit Hilfe der Software ausgewertet und dokumentiert.

Die Vornahme einer solchen Messung ist sehr einfach. Für einigermaßen zuverlässige Messergebnisse müssen folgende Voraussetzungen erfüllt werden:

• Temperaturdifferenz zwischen Innen und Außen, ideal >15 K
• konstante Bedingungen
• keine Sonneneinstrahlung
• keine Heizstrahlung im Messbereich

Es eignen sich daher vornehmlich die Nacht- oder frühen Morgenstunden vor Sonnenaufgang. Dies gilt auch für die Thermografie, welche in der Vergangenheit ebenfalls für die überschlägige Ermittlung des U-Wertes angewandt wurde.

Die Vergleichbarkeit der Ergebnisse sowie die Relevanz des U-Wertes für die Beurteilung der Wärmeverluste eines Gebäudes wird trotz eindeutiger Messungen von Einigen bestritten, z.B. ^[6], sogar dann, wenn sie selbst an den Messungen teilgenommen haben (Bossert) ^[7].

Typische Werte des Bauwesens

Beispielwerte von Wärmedurchgangskoeffizienten

Baustoff	Wandstärke	U-Wert in W/(m²K)
Außenwand aus Beton ohne Wärmedämmung	25 cm	3,3
Außenwand aus Mauerziegeln	24 cm	ca. 1,5
Außenwand aus Mauerziegeln	36,5 cm	ca. 0,8
Außenwand aus Mauerziegeln (36,5 cm) mit Wärmedämmverbundsystem (PUR)	49 cm	ca. 0,32
Außenwand aus hochporösem Hochlochziegel, unverputzt	50 cm	0,17 - 0,23
Außenwand Holzrahmenbau, wohnungstypischer Aufbau	25 cm	0,15 - 0,20
Außenwand aus Massivholz (ohne Wärmedämmung)	20,5 cm	0,5
Innenwand aus Mauerziegeln	11,5 cm	3,0
Innenwand aus Porenbeton	28 cm	ca. 0,6
Außentür aus Holz oder Kunststoff	-	3,49
Acrylglas (Plexiglas)	5 mm	5,3
Einfachfenster	-	5,9
Doppelfenster	-	3,0
Fenster mit Isolierverglasung	-	2,8-3,0
Fenster mit Wärmeschutzverglasung	-	ca. 1,1
Lichtbauelement aus Polycarbonat	5 cm	ca. 0,83
Fenster im Passivhausstandard	-	0,5-0,8

Bedeutung für den Wärmeschutz

Nach der am 1. Februar 2002 in Deutschland in Kraft getretenen und zum 7. Dezember 2004 novellierten Energieeinsparverordnung (EnEV) müssen der Jahres-Primärenergiebedarf Q_P und der spezifische Transmissionswärmeverlust H_T' eines Gebäudes bestimmte Grenzwerte einhalten. U-Werte gehen in die Berechnung des Transmissionswärmeverlustes ein und dieser wiederum in die Berechnung des Primärenergiebedarfs. Ferner schreibt die EnEV Grenzwerte des Wärmedurchgangskoeffizienten bestimmter Bauteile vor, wenn diese neu eingebaut oder ausgetauscht werden.

Siehe auch

• Metalle
• Elektrischer Leiter
• Bändermodell
• Wärmedurchgang
• Wärmedurchlasskoeffizient
• Thermografie

Normen

• EN ISO 6946, als DIN :1996-11 Bauteile – Wärmedurchlaßwiderstand und Wärmedurchgangskoeffizient - Berechnungsverfahren
• EN ISO 7345, als DIN :1996-01 Wärmeschutz – Physikalische Größen und Definitionen (ersetzt DIN 4108-1)
• EN ISO 9346, als DIN :1996-08: Wärmeschutz – Stofftransport – Physikalische Größen und Definitionen
• EN 12524 Baustoffe und -produkte – Wärmeschutztechnische Eigenschaften – Tabellierte Bemessungswerte
• DIN 4108 Wärmeschutz im Hochbau, stellt weitere Anforderungen an U-Werte von Bauteilen, jedoch nicht mit dem Ziel der Energieeinsparung, sondern der Vermeidung von Bauschäden (Mindestwärmeschutz)

Literatur

• W. Heindl: Der Wärmeschutz einer ebenen Wand bei periodischen Wärmebelastungen (1. Teil). Die Ziegelindustrie, Heft 18, 1966, S. 685–693
• W. Heindl: Zum instationären Wärmeverhalten von Wärmebrücken - Oder: Hat die Wärmespeicherfähigkeit von Bauteilen bei mehrdimensionaler Wärmeleitung einen Einfluß auf die Transmissionswärmeverluste?. BAUPHYSIK, Heft 4, 1982, S. 145f.
• M. Reick, S. Palecki: Auszug aus den Tabellen und Formeln der DIN EN ISO 6946. Institut für Bauphysik und Materialwissenschaft. Universität GH Essen. Stand: 10-1999. (Webdokument, PDF 168 KB)
• T. Richter, S. Winkelmann-Fouad: Anwendung des U-Wertes als Kenngröße für Wärmetransportvorgänge. In: E. Cziesielski (Hrsg.): Bauphysikkalender 2005. Ernst & Sohn, Berlin 2005, ISBN 3-433-01722-0

Weblinks

• Einfach zu bedienende U-Wert-Berechnung auf www.energiesparhaus.at

Einzelnachweise

1. ↑ ^{a b} EN ISO 6946 nach Reick, Palecki; siehe Normen und Literatur
2. ↑ W. Heindl: Der Wärmeschutz einer ebenen Wand bei periodischen Wärmebelastungen (1. Teil). Die Ziegelindustrie, Heft 18, 1966, S. 685–693
3. ↑ W. Heindl: Zum instationären Wärmeverhalten von Wärmebrücken - Oder: Hat die Wärmespeicherfähigkeit von Bauteilen bei mehrdimensionaler Wärmeleitung einen Einfluß auf die Transmissionswärmeverluste?. BAUPHYSIK, Heft 4, 1982, S. 145f
4. ↑ Ebel, J.: Der U-Wert: nur stationär oder auch instationär. bauzeitung 56(2002) H. 3, S. 56 - 60
5. ↑ Ebel, J.: EnEV, Solarstrahlung und Boltzmannsche Emission. Bauphysik 25(2003) H. 5, S. 306 - 310
6. ↑ Bausanierung von Guido F. Moschig, Vieweg+Teubner Verlag 2008, ISBN 3835101838, S.101f
7. ↑ EMPA: Einfluß der Wärmespeicherfähigkeit der Aussenwand auf den Sonnenenergiegewinn. EMPA-Untersuchungsbericht Nr. 136'788. Dezember 1994