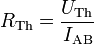Thevenin-Theorem

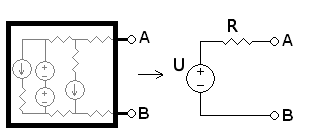
In der Theorie linearer elektrischer Netzwerke besagt das Thévenin-Theorem (auch Helmholtz-Thévenin-Theorem), dass jede mögliche Kombination von Spannungsquellen, Stromquellen und Widerständen bezüglich zweier Klemmen elektrisch äquivalent zu einer Reihenschaltung aus einer Spannungsquelle und einem Widerstand R ist. Diese Ersatzschaltung wird Thévenin-Äquivalent oder im deutschen Sprachraum Ersatzspannungsquelle genannt. Dieses Theorem wird zum Beispiel zur Vereinfachung in der Schaltkreisanalyse verwendet.

Jede elektrische Schaltung, die ausschließlich aus Spannungsquellen, Stromquellen und Widerständen besteht, kann in ein Thévenin-Äquivalent umgewandelt werden.

Berechnung des Thévenin-Äquivalents

Das Thévenin-Äquivalent besteht aus einem Widerstand R_Th und einer Spannungsquelle U_Th. Um die zwei Unbekannten R_Th und U_Th zu bestimmen, benötigt man zwei Gleichungen. Diese Gleichungen können auf verschiedene Art und Weise erstellt werden. Meistens gebraucht man jedoch folgende:

• Die Ausgangsspannung U_AB bei offenen Klemmen A-B, d. h. ohne Lastwiderstand, bestimmen. Diese Leerlaufspannung ist die Thévenin-Äquivalentspannung U_Th.

Um den Thévenin-Äquivalentwiderstand R_Th zu bestimmen, benutzt man meistens eine der drei folgenden Methoden:

• Man ersetzt alle unabhängigen Spannungsquellen durch Kurzschlüsse (behält jedoch die Innenwiderstände) und streicht alle unabhängigen Stromquellen (d. h. man ersetzt sie durch Open Circuits bzw. Unterbrechungen). Gesteuerte (abhängige) Strom- bzw. Spannungsquellen sind jedoch in der Schaltung zu belassen! Dann berechnet man den Ersatzwiderstand. Dieser ist gleich dem Thévenin-Äquivalentwiderstand.
• Wenn man den Kurzschlussstrom I_AB kennt, benutzt man das Ohmsche Gesetz, um R_Th zu bestimmen:

$R_\mathrm{Th} = \frac{U_\mathrm{Th}}{I_\mathrm{AB}}$

• Man schließt einen Widerstand mit bekanntem Wert an A-B an. Mit Hilfe des Spannungsteilergesetzes kann man dann den Thévenin-Äquivalentwiderstand R_Th bestimmen.

Eine geläufige Variante dieser Methode ist die der Halb-Spannung: Man schließt einen veränderbaren Widerstand (ein Potentiometer) an A-B an und misst die Spannung. Dann variiert man den Wert des veränderbaren Widerstandes, bis man die Hälfte der Leerlaufspannung U_Th über A-B misst. Der veränderliche Widerstand ist dann gleich dem Thévenin-Äquivalentwiderstand R_Th.

Beweis des Thévenin-Theorems

Der Beweis des Thévenin-Theorems basiert auf dem Überlagerungsprinzip.

In diesem Artikel oder Abschnitt fehlen folgende wichtige Informationen: siehe Diskussion Du kannst Wikipedia helfen, indem du sie recherchierst und einfügst.

Umsetzung zwischen Norton- und Thévenin-Äquivalent

Norton-Thévenin-Äquivalent-Umwandlung

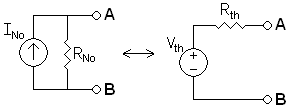
Ein Norton-Äquivalent kann in ein Thévenin-Äquivalent umgewandelt werden anhand folgender Gleichungen:

R_Th = R_No

U_Th = I_NoR_No

Erweiterung für Wechselstrom

Das Norton-Theorem kann auch auf Einfrequenz-Wechselstromsysteme verallgemeinert werden, indem man statt der ohmschen Widerstände eine Impedanz verwendet.

Geschichte

Das Thévenin-Theorem wurde zuerst vom deutschen Wissenschaftler Hermann von Helmholtz 1853 entdeckt. Es wurde dann 1883 vom französischen Ingenieur Léon Charles Thévenin (1857-1926) wiederentdeckt.

Siehe auch

• Elektrizität
• Norton-Theorem
• Kirchhoffsche Regeln
• Ohmsches Gesetz
• Überlagerungsprinzip
• Millman-Theorem
• Open circuit
• Spannungsteiler
• Parallelschaltung
• Reihenschaltung
• Stern-Dreieck-Transformation