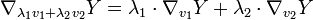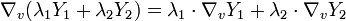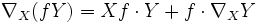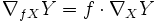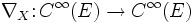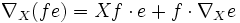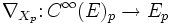- Affiner Zusammenhang
-
Im mathematischen Teilgebiet der Differentialgeometrie ist ein Zusammenhang ein Hilfsmittel, um Richtungsänderungen im Laufe einer Bewegung zu quantifizieren und Richtungen in verschiedenen Punkten miteinander in Beziehung zu setzen.
Dieser Artikel behandelt im Wesentlichen den Spezialfall des affinen Zusammenhangs auf einer differenzierbaren Mannigfaltigkeit und daneben den des linearen Zusammenhangs auf einem Vektorbündel. Allgemeiner existieren Zusammenhänge auf Faserbündeln.
Inhaltsverzeichnis
Definition: Zusammenhang auf dem Tangentialbündel (affiner Zusammenhang)
Ein Zusammenhang auf einer differenzierbaren Mannigfaltigkeit M wird dadurch angegeben, dass man angibt, was die Richtungsableitung eines Vektorfelds in Richtung eines Tangentialvektors sein soll. Demgemäß definiert man einen Zusammenhang auf dem Tangentialbündel von M als eine Abbildung
 , die einem Tangentialvektor
, die einem Tangentialvektor 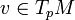 in einem Punkt
in einem Punkt 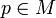 und einem in einer Umgebung von p definierten differenzierbaren Vektorfeld Y einen Tangentialvektor
und einem in einer Umgebung von p definierten differenzierbaren Vektorfeld Y einen Tangentialvektor 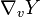 (die kovariante Ableitung von Y an der Stelle p in Richtung von v) zuordnet, so dass die folgenden Bedingungen erfüllt sind:
(die kovariante Ableitung von Y an der Stelle p in Richtung von v) zuordnet, so dass die folgenden Bedingungen erfüllt sind: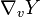 hängt linear und differenzierbar von
hängt linear und differenzierbar von 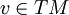 ab.
ab.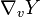 ist
ist  -linear in Y.
-linear in Y.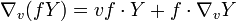
-
- für jede in einer Umgebung von p definierte differenzierbare Funktion f.
Ausführlicher formuliert besteht die erste Bedingung aus den folgenden beiden Punkten:
-
- für
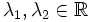 und
und 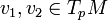
- für
- Ist X ein differenzierbares lokales Vektorfeld, so ist
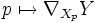 ein differenzierbares Vektorfeld.
ein differenzierbares Vektorfeld.
Die zweite Bedingung bedeutet:
-
- für
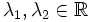 und lokale Vektorfelder Y1,Y2.
und lokale Vektorfelder Y1,Y2.
- für
Die dritte Bedingung entspricht der Produktregel beim Differenzieren. Mit vf wird dabei die Richtungsableitung der Funktion f in Richtung des Vektors v bezeichnet. Insgesamt verhält sich ein Zusammenhang also so, wie man es von einem Ableitungsoperator erwartet.
Eine äquivalente Beschreibung charakterisiert Zusammenhänge als Abbildungen
 , die zwei lokalen differenzierbaren Vektorfeldern X,Y ein lokales differenzierbares Vektorfeld
, die zwei lokalen differenzierbaren Vektorfeldern X,Y ein lokales differenzierbares Vektorfeld 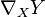 zuordnet, so dass
zuordnet, so dass 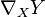
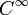 -linear in X und
-linear in X und  -linear in Y ist, und so dass
-linear in Y ist, und so dassfür lokale differenzierbare Funktionen f gilt. Dabei bedeutet
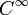 -linear, dass
-linear, dass 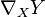 additiv in X ist und
additiv in X ist undfür lokale differenzierbare Funktionen f gilt.
Wichtigstes Beispiel für einen Zusammenhang ist der Levi-Civita-Zusammenhang, der es einem auf riemannschen Mannigfaltigkeiten erlaubt, ein Vektorfeld in Richtung eines anderen zu abzuleiten.
Darstellung in Koordinaten: Christoffel-Symbole
Bilden die lokalen Vektorfelder
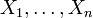 in jedem Punkt eine Basis des Tangentialraums, so sind die Christoffel-Symbole definiert durch
in jedem Punkt eine Basis des Tangentialraums, so sind die Christoffel-Symbole definiert durch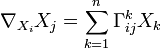 bzw.
bzw. 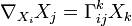 in einsteinscher Summenkonvention.
in einsteinscher Summenkonvention.
Haben die Vektorfelder X und Y bezüglich dieser Basis die Gestalt X = xiXi und Y = yjXj, so gilt für die Komponenten zk von
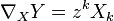
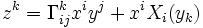 ,
,
wobei Xi(yk) die Richtungsableitung der Funktion yk in Richtung des Vektors Xi bezeichnet.
Wählt man als Basisvektorfelder speziell die durch eine Karte gegebenen Vektorfelder
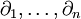 , so erhält man die Koordinatendarstellung
, so erhält man die Koordinatendarstellung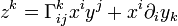 .
.
Definition: Zusammenhang auf einem Vektorbündel (linearer Zusammenhang)
Ist M eine differenzierbare Mannigfaltigkeit und E ein Vektorbündel auf M, so ist ein Zusammenhang auf E eine Abbildung
 , die einem lokalen differenzierbaren Vektorfeld X von Tangentialvektoren der Mannigfaltigkeit M eine
, die einem lokalen differenzierbaren Vektorfeld X von Tangentialvektoren der Mannigfaltigkeit M eine  -lineare Abbildung
-lineare Abbildungzuordnet, die
für lokale Funktionen f und lokale Schnitte e erfüllt. Außerdem soll
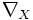 ,
, 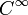 -linear in X sein.
-linear in X sein.Ähnlich wie oben ist auch eine lokalisierte Version dieser Definition mithilfe von Abbildungen
für Tangentialvektoren
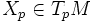 möglich.
möglich.Siehe auch
Wikimedia Foundation.