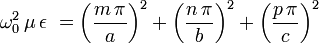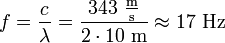Beckenresonator

Ein Hohlraumresonator verwendet Resonanz zur Verstärkung einer Welle. Dabei sind die Innenwände derart ausgerichtet, dass Reflexion einer Welle zwischen ihnen möglich ist. Wenn eine mit dem Hohlraum resonante Welle in diesen eintritt, wird sie im Hohlraum verlustarm hin und her reflektiert (siehe: Beckenschwingung, Stehende Welle). Je mehr Wellenenergie in den Hohlraum gelangt, desto besser überträgt sich diese auf die stehende Welle und verstärkt deren Intensität.

Beispiele für Hohlraumresonatoren:

• Mikrowellen: Ein- und Auskoppel-Resonatoren in Klystrons, Wellenmesser
• Luft-Schall: Die Rohre von Flöten und anderen Blasinstrumenten, Bassreflexbox, Resonanzen in Wohnräumen, Helmholtz-Resonator, Kundtsches Rohr, Orgelpfeifen

Hohlraumresonatoren in der Hochfrequenztechnik

Hohlraumresonatoren spielen in der Hochfrequenztechnik eine wichtige Rolle. Mit Hilfe von Hohlraumresonatoren lassen sich gute Filter auch für sehr hohe Frequenzen entwickeln.

Die Resonanzfrequenzen eines rechteckigen Hohlraumresonators lassen sich mit folgender Gleichung berechnen:

$\omega_0^2 \, \mu \, \epsilon\ = \left( \frac{m\,\pi}{a}\right)^2+\left(\frac{n\,\pi}{b}\right)^2+\left(\frac{p\,\pi}{c}\right)^2 \,$

wobei einer der positiv ganzzahligen Parameter m, n, oder p auf Null gesetzt werden darf und a, b und c die Abmessungen sind.

Ein Hohlraumresonator hat somit eine unendliche Anzahl von Resonanzfrequenzen.

Die niedrigsten Resonanzfrequenzen lassen sich noch gut trennen. Höhere Resonanzfrequenzen liegen jedoch immer dichter beieinander und gehen sogar ineinander über. Dadurch ist eine Trennung aufgrund der endlichen Bandbreite nicht mehr möglich.

Man nennt dieses die Resonanzfrequenzdichte.

Um eine Resonanz im Hohlraumresonator hervorzurufen, muss Energie zugeführt werden. Da Hohlraumresonatoren eine Dämpfung besitzen, klingt diese Resonanz wieder ab, wenn keine Energie mehr zugeführt wird. Die Energie wird in der Regel durch eine Form des Wellenleiters zugeführt. Die Ankopplung des Wellenleiters ist abhängig von der Art des Wellenleiters und der Modi, die angeregt werden sollen und lässt sich in kapazitive und induktive Ankopplung einteilen.

Beispiel-Berechnung der Resonanzfrequenzen:

Hohlraumresonator mit den Abmessungen: a = 30 cm, b = 20 cm und c = 10 cm

m	n	p	f0
1	1	0	901,4 MHz
2	1	0	1,25 GHz
1	0	1	1,58 GHz
0	1	1	1,68 GHz
3	1	0	1,68 GHz

Licht und Laser

In einem Laser, wird Licht einer bestimmten Frequenz in einem Hohlraumresonator verstärkt, der gewöhnlich aus einer Anordnung aus zwei oder – bei gefaltetem Resonator – aus mehreren Spiegeln besteht. Hier wie auch beim Fabry-Pérot-Interferometer läuft das Licht nur in einer Richtung zwischen den Spiegeln hin- und her. Die Eigenresonanzen heißen beim Laser Longitudinalmoden. Liegen mehrere dieser Moden innerhalb des Verstärkungsbereiches des aktiven Mediums des Lasers, kann dieser zugleich oder wahlweise auf einer dieser diskreten Moden bzw. Frequenzen arbeiten. Bei der Modenkopplung (mode locking) sind mehrerer dieser Moden synchronisiert und überlagern sich zu einem hin- und herlaufenden Impuls.

Hohlraumresonatoren in der Akustik

In der Akustik spielen beidseitig und einseitig offene sowie geschlossene Hohlraumresonatoren eine große Rolle.

Beidseitig offene Rohre besitzen ihre Grundresonanz bei der halben Schallwellenlänge.

Beispiele für beidseitig offene Resonatoren sind:

• Flöte: durch Blastechnik und Griffe können die Grundwelle und geradzahlige Harmonische (eine oder mehrere Oktaven höher) angeregt werden. Die effektive Rohrlänge wird durch die mit den Fingern hintereinander geschlossenen Löcher bestimmt.
• Resonanzrohre unter den Tönen von Xylophonen und Metallophonen
• Kundtsches Rohr

Einseitig offene Rohre besitzen ihre Grundresonanz bei einem Viertel der Schallwellenlänge:

• gedackte Orgelpfeifen, Posaunen, Trompeten; hier sind ungeradzahlige Oberwellen bzw. geradzahlige Harmonische anregbar.

Geschlossene Resonatoren:

• Resonanzen in geschlossenen Räumen: während kleine Räume ausgesprochen diskrete Eigenfrequenzen aufweisen, überlagern sich bei großen Räumen (z.B. Kirchen) alle Moden zu einem Kontinuum - es tritt Hall auf.

Beim Helmholtz-Resonator und bei Bassreflexboxen unterliegen die Grundresonanzen anderen Gesetzen; hier schwingt die Luftmasse im Hals bzw. im Bassreflexrohr gegen die Elastizität des Volumens, die Grundresonanzen sind niedriger als es die geometrischen Abmessungen erwarten lassen.

Orgelpfeifen gibt es in zwei Ausführungen: am Ende offen oder geschlossen (gedackt).

Eine 10 m lange, offene Pfeife erzeugt einen Ton mit einer Frequenz von

$f = \frac{c}{\lambda} = \frac{343~\frac{\rm m}{\rm s}}{2 \cdot 10~{\rm m}}\approx 17~{\rm Hz} \,$

(f = Frequenz, c = Schallgeschwindigkeit 343 m/s bei 20°C und λ = Wellenlänge). Eine gedackte Pfeife muss nur halb so lang sein, um einen Ton mit der gleichen Frequenz zu erzeugen. Sie entwickelt jedoch andere Obertöne bzw. Harmonische: während eine offene Pfeife alle Harmonische bzw. Obertöne enthält, sind es bei einer gedacken Orgelpfeife ungradzahlige Teiltöne (Partialtöne, Harmonische), also Vielfache der Grundfrequenz 3f, 5f, 7f, … bzw. geradzahlige Obertöne, die herausragen. Ungeradzahlige Harmonische, Partialtöne oder Teiltöne sind eben geradzahlige Obertöne.

Resonanz bei Oberflächenwellen

Bei Wasserwellen und anderen Oberflächenwellen (Schwerewellen bzw. Rayleigh-Wellen) kann in ähnlicher Weise von einem zweidimensionalen Resonator gesprochen werden, wenn die Flächen reflektierend begrenzt sind:

Für Tideresonanz stellt die in einer Bucht schwingfähige Wassermasse einen sogenannten Beckenresonator dar; siehe auch Beckenschwingung, Seiche.

Bei Wellenresonanzen können vom erregenden Wellenspektrum gleichzeitig mehrere Eigenfrequenzen einer zwischen der Küste und vorgelagerten Riffen schwingfähigen Wassermasse getroffen werden, sodass dieselbe Wassermasse unterschiedliche Beckenresonanzen ausführt.

Resonanz und Interferenz akustischer Wellen in Festkörpern werden in Schwingquarzen und Oberflächenwellenfiltern genutzt.

Schwingquarze und keramische Resonatoren können auch auf ihren Harmonischen zum Schwingen angeregt werden.