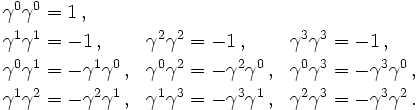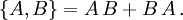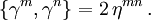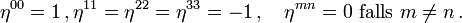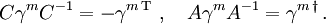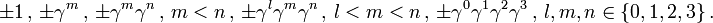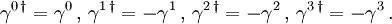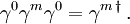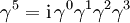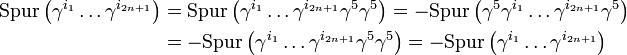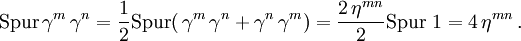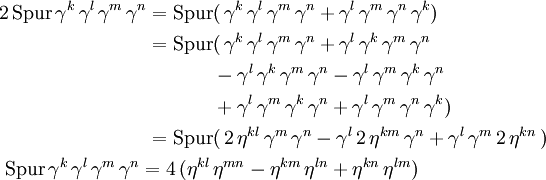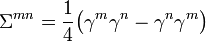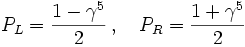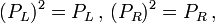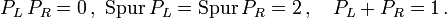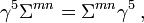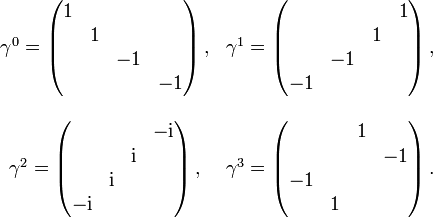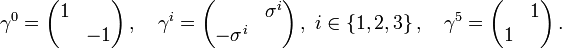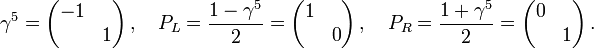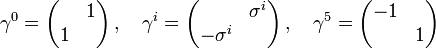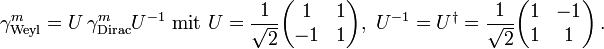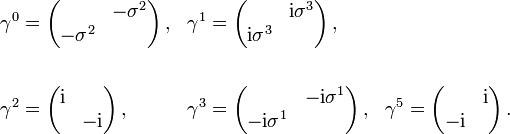Weyl-Darstellung

Die Dirac-Matrizen (auch Gamma-Matrizen genannt) sind vier Matrizen, die der Dirac-Algebra genügen. Sie treten in der Dirac-Gleichung auf.

Definition

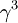Die Dirac-Matrizen $\gamma^0,\,\gamma^1\,,\gamma^2\,$ und $\,\gamma^3\,$ erfüllen definitionsgemäß die Dirac-Algebra, das heißt, die algebraischen Bedingungen

$\begin{align} \gamma^0\gamma^0 &= 1\,, &&&&&\\ \gamma^1\gamma^1 &= -1\,,&\gamma^2\gamma^2 &= -1\,,&\gamma^3\gamma^3 &= -1\,,\\ \gamma^0\gamma^1 &= -\gamma^1\gamma^0\,, & \gamma^0\gamma^2 &= -\gamma^2\gamma^0\,, & \gamma^0\gamma^3 &= -\gamma^3\gamma^0\,, \\ \gamma^1\gamma^2 &= -\gamma^2\gamma^1\,, & \gamma^1\gamma^3 &= -\gamma^3\gamma^1\,, & \gamma^2\gamma^3 &= -\gamma^3\gamma^2\,. \end{align}$

Diese Bedingungen betreffen Antikommutatoren, also die Summe der Produkte zweier Matrizen in beiden Reihenfolgen,

$\{ A , B \} = A\,B + B\,A\,.$

In Indexnotation, in der m und n für Zahlen aus {0,1,2,3} stehen, schreiben sich die Bedingungen an die Dirac-Matrizen zusammenfassend als

$\{ \gamma^m , \gamma^n \} = 2\,\eta^{mn}\,.$

Dabei sind η^mn die Komponenten der Minkowski-Metrik

$\eta^{00}=1\,,\eta^{11}=\eta^{22}=\eta^{33}=-1\,,\quad \eta^{mn}=0\text{ falls }m\ne n\,.$

Eigenschaften

Die Gamma-Matrizen erzeugen eine Clifford-Algebra. Jede irreduzible Darstellung dieser Algebra durch Matrizen besteht aus 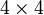$4\times 4$-Matrizen. Die Elemente des Vektorraumes, auf den sie wirken, heißen Spinoren. Verschiedene Darstellungen der Dirac-Algebra sind einander äquivalent, das heißt, sie unterscheiden sich nur durch die gewählte Basis. Insbesondere sind die negativen transponierten Matrizen 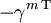$-\gamma^{m\,\text{T}}$ und die hermitesch adjungierten Matrizen 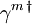$\gamma^{m\,\dagger}$ den Matrizen 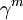$\,\gamma^m\,$ äquivalent, denn sie erfüllen ebenfalls die Dirac-Algebra. Es gibt daher eine Matrix A und eine Matrix C, so dass

$C \gamma^m C^{-1}=-\gamma^{m\,\text{T}}\ ,\quad A \gamma^m A^{-1}=\gamma^{m\,\dagger}\,.$

Die Matrix A ist zur Konstruktion von Skalaren, Vektoren und Tensoren aus Spinoren wichtig, die Matrix C tritt bei der Ladungskonjugation auf.

Jedes Produkt mehrerer Dirac-Matrizen lässt sich bis auf ein Vorzeichen als Produkt verschiedener Dirac-Matrizen in lexographischer Ordnung schreiben, denn das Produkt zweier verschiedener Gamma-Matrizen kann auf Kosten eines Vorzeichens umgeordnet werden. Zudem ist das Quadrat jeder Gamma-Matrix 1 oder -1. Die Produkte verschiedener Gamma-Matrizen bilden zusammen mit der Eins-Matrix und den negativen Matrizen eine Gruppe mit den 32 Elementen,

$\pm 1\,,\, \pm \gamma^m\,,\, \pm \gamma^m \gamma^n\,,\,m<n\,,\, \pm \gamma^l \gamma^m \gamma^n \,,\,l<m<n\,,\, \pm \gamma^0 \gamma^1 \gamma^2 \gamma^3\,,\,l,m,n\in\{0,1,2,3\}\,.$

Da jede Darstellung einer endlichen Gruppe bei geeigneter Basiswahl unitär ist, ist auch jede Darstellung der Gamma-Matrizen bei geeigneter Wahl der Basis unitär. Zusammen mit der Dirac-Algebra heißt dies, dass γ⁰ hermitesch und die drei anderen γ-Matrizen antihermitesch sind,

$\gamma^{0\,\dagger}=\gamma^0\,,\,\gamma^{1\,\dagger}=-\gamma^1\,,\,\gamma^{2\,\dagger} =-\gamma^2\,,\,\gamma^{3\,\dagger}=-\gamma^3\,.$

In unitären Darstellungen bewirkt A = γ⁰ die Äquivalenztransformation zu den adjungierten Matrizen

$\gamma^0 \gamma^m \gamma^0=\gamma^{m\,\dagger}\,.$

Die Matrix

$\gamma^5=\mathrm i\, \gamma^0 \gamma^1 \gamma^2 \gamma^3$

ist ihr eigenes Inverses, 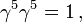$\gamma^5 \gamma^5 = 1\,,$ ist hermitesch, antivertauscht mit den Gamma-Matrizen, γ⁵γ^m = − γ^mγ⁵, und demnach mit jedem Produkt von Gamma-Matrizen mit einer ungeraden Anzahl von Faktoren.

Daher verschwindet die Spur jedes Produktes von Gamma-Matrizen mit einer ungeraden Anzahl von Faktoren.

$\begin{align} \text{Spur}\, \bigl(\gamma^{i_1}\dots \gamma^{i_{2n+1}}\bigr)&= \text{Spur}\, \bigl(\gamma^{i_1}\dots \gamma^{i_{2n+1}}\gamma^5\gamma^5\bigr)= -\text{Spur}\, \bigl(\gamma^5\gamma^{i_1}\dots \gamma^{i_{2n+1}}\gamma^5\bigr)\\ &= -\text{Spur}\, \bigl(\gamma^{i_1}\dots \gamma^{i_{2n+1}}\gamma^5\gamma^5\bigr)= -\text{Spur}\, \bigl(\gamma^{i_1}\dots \gamma^{i_{2n+1}}\bigr) \end{align}$

Im vorletzten Schritt haben wir dabei verwendet, dass die Spur eines Produktes sich bei zyklischer Vertauschung der Faktoren nicht ändert und demnach 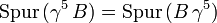$\text{Spur}\,(\gamma^5\,B)= \text{Spur}\,(B\,\gamma^5)$ gilt.

Für die Spur eines Produktes von zwei Gamma-Matrizen gilt (weil die Spur zyklisch ist)

$\text{Spur}\,\gamma^{m}\,\gamma^{n} = \frac 1 2 \text{Spur}(\,\gamma^{m}\,\gamma^{n} +\gamma^{n}\,\gamma^{m}) = \frac{2\, \eta^{mn}}{2} \text{Spur 1} = 4 \,\eta^{mn}\,.$

Die Spur von vier Gamma-Matrizen reduziert man mit der Dirac-Algebra auf die Spur von zwei.

$\begin{align} 2\,\text{Spur}\,\gamma^k \,\gamma^l\,\gamma^{m}\,\gamma^{n}= \text{Spur}&(\,\gamma^k \,\gamma^l\,\gamma^{m}\,\gamma^{n}+\gamma^l\,\gamma^{m}\,\gamma^{n}\,\gamma^k )\\ = \text{Spur}&(\,\gamma^k \,\gamma^l\,\gamma^{m}\,\gamma^{n} + \gamma^l \,\gamma^k\,\gamma^{m}\,\gamma^{n}\\ & -\gamma^l \,\gamma^k\,\gamma^{m}\,\gamma^{n} -\gamma^l \,\gamma^m\,\gamma^k\,\gamma^{n}\\ &+\gamma^l \,\gamma^m\,\gamma^k\,\gamma^{n} +\gamma^l \,\gamma^m\,\gamma^n\,\gamma^{k})\\ = \text{Spur}&(\, 2\,\eta^{kl}\,\gamma^m\,\gamma^n - \gamma^l\,2\,\eta^{km}\,\gamma^n +\gamma^l\,\gamma^m\,2\,\eta^{kn}\, )\\ \text{Spur}\,\gamma^k \,\gamma^l\,\gamma^{m}\,\gamma^{n}= 4\, (\eta^{kl}\,&\eta^{mn} -\eta^{km}\,\eta^{ln} +\eta^{kn}\,\eta^{lm}) \end{align}$

Falls also verschiedene Dirac-Matrizen in einem Produkt nicht paarweise auftauchen, verschwindet die Spur des Produktes. Daraus folgt unter anderem, dass die sechzehn Matrizen, die man als Produkt von Null bis vier verschiedenen Gamma-Matrizen erhält, linear unabhängig sind.

Zusammenhang zu Lorentztransformationen

Die sechs Matrizen

$\Sigma ^{mn} = \frac{1}{4}\bigl( \gamma^m \gamma^n - \gamma^n \gamma^m\bigr)$

bilden die Basis einer Lie-Algebra, die der Lie-Algebra der Lorentztransformationen isomorph ist. Sie erzeugen die zu Lorentztransformationen (die stetig mit der 1 zusammenhängen) gehörigen Transformationen der Spinoren ψ.

Aus (γ⁵)² = 1 und 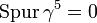$\text{Spur}\,\gamma^5=0$ folgt, dass die Matrizen

$P_L = \frac{1-\gamma^5}{2}\,,\quad P_R = \frac{1+\gamma^5}{2}$

Projektoren sind,

$(P_L)^2=P_L\,,\,(P_R)^2=P_R\,,$

die auf zueinander komplementäre, zweidimensionale Unterräume projizieren,

$P_L\,P_R=0\,,\ \text{Spur}\,P_L=\text{Spur}\,P_R=2\,,\quad P_L+P_R=1\,.$

Weil γ⁵ mit den Erzeugenden von Spinortransformationen vertauscht,

$\gamma^5 \Sigma^{mn}= \Sigma^{mn}\gamma^5\,,$

sind die Unterräume, auf die P_L und P_R projizieren, invariant unter den von Σ^mn erzeugten Lorentztransformationen, mit anderen Worten: Die links- und rechtshändigen Anteile, ψ_L = P_Lψ und ψ_R = P_Rψ, eines Spinors ψ transformieren getrennt voneinander.

Die Spinortransformation führt bei Größen, die man aus 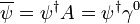$\overline{\psi}=\psi^\dagger A=\psi^\dagger \gamma^0$, Gamma-Matrizen und einem eventuell von ψ verschiedenen Spinor χ zusammensetzt, zu einem Transformationsgesetz, das am Indexbild ablesbar ist. Es transformieren

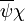• $\overline \psi \chi$ wie ein Skalar,
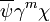• $\overline \psi\gamma^m \chi$ wie die Komponenten eines Vierervektors,
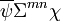• $\overline \psi\Sigma^{mn} \chi$ wie die Komponenten eines antisymmetrischen Tensors,
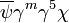• $\overline \psi\gamma^m\gamma^5 \chi$ wie die Komponenten eines axialen Vierervektors,
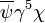• $\overline \psi\gamma^5 \chi$ wie ein Pseudoskalar.

Dirac-Darstellung

In einer geeigneten Basis haben die Gamma-Matrizen die auf Dirac zurückgehende Form (wir schreiben verschwindende Matrixelemente nicht aus)

$\begin{array}{c c} \gamma^0 = \begin{pmatrix} 1 & & & \\ & 1 & & \\ & & -1 & \\ & & & -1 \end{pmatrix}\,,& \gamma^1 = \begin{pmatrix} & & & 1 \\ & & 1 & \\ & -1 & & \\ -1 & & & \end{pmatrix}\,,\\ \,& \,\\ \gamma^2 = \begin{pmatrix} & & & -\mathrm i \\ & & \mathrm i & \\ & \mathrm i & & \\ -\mathrm i & & & \end{pmatrix}\,, & \gamma^3 = \begin{pmatrix} & & 1 & \\ & & & -1 \\ -1 & & & \\ & 1 & & \end{pmatrix} \,. \end{array}$

Diese Matrizen lassen sich kompakter mit Hilfe der Pauli-Matrizen schreiben (jeder Eintrag steht hier für eine $2 \times 2$-Matrix):

$\gamma^0 = \begin{pmatrix} 1 & \\ & -1 \end{pmatrix}\,,\quad \gamma^i = \begin{pmatrix} & \sigma^i \\ -\sigma^i & \end{pmatrix}\, ,\;i\in\{1,2,3\}\,,\quad \gamma^5 = \begin{pmatrix} & 1 \\ 1 & \end{pmatrix}\,.$

Weyl-Darstellung

Die nach Hermann Weyl benannte Weyl-Darstellung heißt auch chirale Darstellung. In ihr ist γ⁵ diagonal,

$\gamma^5 = \begin{pmatrix} -1 & \\ & 1 \end{pmatrix}\,,\quad P_L = \frac{1-\gamma^5}{2} = \begin{pmatrix} 1 & \\ & 0 \end{pmatrix}\,,\quad P_R = \frac{1+\gamma^5}{2} = \begin{pmatrix} 0 & \\ & 1 \end{pmatrix}\,.$

Im Vergleich zur Dirac-Darstellung ist einfach γ⁰ durch γ⁵ und γ⁵ durch − γ⁰ ausgetauscht:

$\gamma^0 = \begin{pmatrix} & 1 \\ 1 & \end{pmatrix}\,,\quad \gamma^i = \begin{pmatrix} & \sigma^i \\ -\sigma^i & \end{pmatrix}\,,\quad \gamma^5 = \begin{pmatrix} -1 & \\ & 1 \end{pmatrix}$

Die Weyldarstellung ergibt sich durch einen unitären Basiswechsel aus der Dirac-Darstellung,

$\gamma^m_{\text{Weyl}}=U\,\gamma^m_{\text{Dirac}}U^{-1}\text{ mit } U= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1\\ -1 & 1 \end{pmatrix},\ U^{-1}=U^\dagger= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & -1\\ 1 & 1 \end{pmatrix}\,.$

Spinortransformationen transformieren in der Weyl-Basis die ersten beiden und die letzten beiden Komponenten des Dirac-Spinors getrennt.

Die chirale Darstellung ist von besonderer Bedeutung in der Weyl-Gleichung, der masselosen Dirac-Gleichung.

Majorana-Darstellung

In der Majorana-Darstellung sind alle Gamma-Matrizen imaginär. Dann ist die Dirac-Gleichung ein reelles Differentialgleichungssystem,

$\begin{align} \gamma^{0} &= \begin{pmatrix} & -\sigma^2 \\ -\sigma^2 & \end{pmatrix}\,,& \gamma^{1} &= \begin{pmatrix} &\mathrm i\sigma^3 \\ \mathrm i\sigma^3 & \end{pmatrix}\,,&\\ &\, & &\\ \gamma^{2}&= \begin{pmatrix} \mathrm i & \\ & -\mathrm i \end{pmatrix}\,,& \gamma^{3} &= \begin{pmatrix} & -\mathrm i\sigma^1 \\ -\mathrm i\sigma^1 & \end{pmatrix}\,,& \gamma^{5} &= \begin{pmatrix} & \mathrm i \\ -\mathrm i & \end{pmatrix}\,. \end{align}$

Dirac-Algebra in höheren Dimensionen

• Ferdinando Gliozzi, Joel Sherk and David Olive, Supersymmetry, Supergravity Theories and the Dual Spinor Model, Nucl. Phys. B122, 253-290, 1977

Bücher

• James Bjorken und Sidney Drell: Relativistische Quantenmechanik, BI-Wissenschaftsverlag, Mannheim, 1990, (BI-Hochschultaschenbuch Band 98), ISBN 3-411-00098-8
• Michael Peskin and Daniel V. Schroeder: An Introduction to Quantum Field Theory, Addison-Wesley Publishing Co., New York, 1995, ISBN 0-201-50397-2
• J. M. Jauch and F. Rohrlich: The theory of photons and electrons, Addison-Wesley Publishing Co., New York, 1955