Nachkommastellen

Die signifikanten Stellen einer Zahl sind die angegebenen Ziffern ohne führende Nullen. Ob endende Nullen signifikant sind, muss fallweise hinterfragt werden; durch geeignete Schreibweise soll hier für Klarheit gesorgt werden.
Die Signifikanz einer Zahl ist die Anzahl der signifikanten Stellen. Sie ist eine Angabe zur Genauigkeit.

Zahlenschreibweise im Zehnersystem

Signifikante Stellen einer Zahl mit Nachkommastellen

Als Nachkommastellen werden die in der dezimalen Darstellung einer Zahl verwendeten Ziffern rechts vom Komma bezeichnet.
Die Anzahl der Nachkommastellen ist zu unterscheiden von der Anzahl der signifikanten Stellen. Aber jede verantwortlich an die Zahl angehängte (nicht leichtfertig vom Taschenrechner übernommene) Nachkommastelle ist eine signifikante Stelle.

Beispiele für Stellen einer Zahl

Zahl	Signifikante Stellen	Nachkommastellen
98,76	4	2
0,009876	4	6

Signifikante Stellen einer ganzen Zahl

Ganze Zahlen haben keine Nachkommastellen.

Schwieriger ist die Aussage zu den signifikanten Stellen: Besitzt „20“ eine, zwei oder sogar mehr signifikante Stellen? Je nach Zusammenhang ist eine Zahl exakt zu werten, wenn sie z. B. als natürliche Zahl verwendet wird; oder sie ist als gerundete Zahl zu werten, wenn sie als Zahlenwert zu einer physikalischen Größe verwendet wird.
Zu einer exakten Zahl stellt sich die Frage nach der Signifikanz nicht, da sie mit beliebig vielen Nachkomma-Nullen verlängert werden kann.
Um zu einer mittels Messtechnik ermittelten Größe beim Zahlenwert „20“ eine Mehrdeutigkeit zu vermeiden, soll man die wissenschaftliche Schreibweise mit Zehnerpotenz-Faktor wählen. Dadurch kann eine endende Null auf eine Nachkommastelle verschoben werden. Eine nicht signifikante Null wird weggelassen; durch das Schreiben der Null wird sie als signifikant gekennzeichnet:

• eine signifikante Stelle: 2 · 10¹
• zwei signifikante Stellen: 2,0 · 10¹
• drei signifikante Stellen: 20,0

Zahl	Signifikante Stellen	Nachkommastellen
9876000,00 · 10−2	9	2
9876000	ungeklärt: 4 bis 7	0
98760 · 102	ungeklärt: 4 oder 5	0
987,6 · 104	4	1
9,876 · 106	4	3
0,09876 · 108	4	5

Definition und Kommaregel

DIN 1333 definiert die signifikanten Stellen als die erste von Null verschiedene Stelle bis zur Rundungsstelle. Diese ist die letzte Stelle, die nach dem Runden noch angegeben werden kann.

Die durch Rundung wegzulassenden Ziffern sollen nicht durch Nullen aufgefüllt werden. Durch Kommaverschiebung und Zehnerpotenz-Faktor ist die Rundungsstelle auf die Einerstelle oder eine Nachkommastelle zu verschieben, siehe auch Messwert.

In der Messtechnik kann die Kommastellung nicht nur durch den Zehnerpotenz-Faktor, sondern auch durch die Wahl der Einheit (z. B. bei Länge mm → cm → m → km) angepasst werden.
Beispiel: Wer statt 20 km lieber 20 000 m schreibt, hat mit endenden Nullen aufgefüllt, die nicht signifikant sind. Falls die Länge doch bis auf wenige Meter genau angebbar ist, wäre zuvor 20,000 km zu schreiben (alle Stellen bis zur Rundungsstelle).

Ergebnis einer Rechnung

Das Ergebnis einer Rechnung ist von der Zahl der signifikanten Stellen, mit denen die Rechnung durchgeführt wird, abhängig:

Zahlen	Signifikante Stellen	Ergebnis
20,567 + 0,0007	5	20,568 (Runden!)
10 + 1,2345	2	11
10,00 + 1,2345	4	11,23
10,000 + 1,2345	5	11,235
1,234 · 3,33	3	4,11

Das Ergebnis ist davon abhängig, ob eine der Zahlen exakt ist, und ob die Anzahl der Stellen vor oder nach der Rechnung fixiert wird:

Zahlen	Signifikante Stellen	Ergebnis
3 · 1,234	1	3 (Vor der Rechnung: 1,234 ≈ 1)
		4 (Nach der Rechnung: 3,702 ≈ 4)
	4	3,702

Welche der Zahlen für die Anzahl der signifikanten Stellen als Maß genommen wird, hängt von ihrer Wertigkeit ab. Im letzten Beispiel etwa kann 3 ein als exakt zu bewertender Parameter sein, und die signifikanten Stellen ergeben sich aus dem Wert 1,234 im Sinne eines Messwertes. Oder die Zahl 1,234 ist der Parameter, dann sind die Stellen der Zahl 3 signifikant, so dass es im Ergebnis auch nur eine signifikante Stelle gibt. Sind die Zahlen beide nicht exakt, muss das Ergebnis auf die niedrigste vorhandene Signifikanz gebracht werden. Oder: Wenn das Ergebnis 3,702 verantwortlich angegeben werden soll, muss für die 3 eine 3,000 verantwortlich angebbar sein!

• Wird etwa ein Durchmesser eines Kreises auf Millimeter genau gemessen, errechnet man den Umfang trotzdem mit einer möglichst genauen Annäherung an Pi, und nicht mit der Zahl 3 oder 3,142. Der Umfang kann trotz der Rechnung mit dem genauen Faktor wieder nur millimetergenau angegeben werden.
• Wird eine Zeichnung etwa im Maßstab 10:1 vergrößert, und die Koordinaten sind millimetergenau gemessen, ist die Vergrößerung zentimetergenau. Signifikante Stellen sind die der Koordinaten, nicht die des Maßstabsfaktors.
• Wird aus zwei gemessenen Seiten eines Dreiecks die dritte Seite errechnet, ist die Signifikanz des schlechteren der beiden Messwerte entscheidend.

Signifikante Stellen in der Messtechnik

Für die Messtechnik ist es immer die sicherste Methode, die Fehlergrenzen der Eingangsdaten zu beachten und ihre Auswirkungen auf das Ergebnis einer Rechnung zu bestimmen, siehe Fehlerfortpflanzung. Exakte Zahlen haben die Fehlergrenze null. Die Fehlergrenze des Ergebnisses liefert die Angabe, wie weit niederwertige Stellen signifikant sind.

Beispiel

Ein Kreisradius wird gemessen zu 17,5 cm. Gesucht wird der Umfang U = 2πr. Im Gegensatz zu oben soll hier π nicht mit sehr vielen Nachkommastellen angegeben werden, sondern nur mit einer Signifikanz passend zur Signifikanz von r.

Exakt: $2 = 2{,}000 \cdot ( 1 \pm 0 %)$

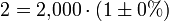
Gerundet: $\pi = 3{,}14 \pm 0{,}005 = 3{,}14 \cdot (1 \pm 0,2 %)$

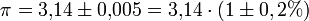
Eine gerundete Zahl kann auf der ersten weggeschnittenen Stelle um ±5 falsch sein.

Gemessen: $r = 17{,}5\,\mathrm{cm} \pm 0{,}1\,\mathrm{cm} = 17{,}5\,\mathrm{cm} \cdot (1 \pm 0{,}6 %)$

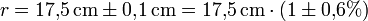
Vom Messwert wird angenommen, dass die niederwertigste Stelle um ±1 falsch angegeben sein kann.

Rechnung: $U = 109{,}90\,\mathrm{cm} \cdot (1 \pm (0 + 0{,}2 + 0{,}6) %) = 109{,}90\,\mathrm{cm} \pm 0{,}9\,\mathrm{cm}$

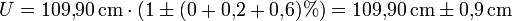
Ergebnis: 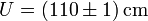$U = (110 \pm 1)\,\mathrm{cm}$, etwas Genaueres lässt sich nicht angeben, denn in diesem Fall ist die erste Nachkommastelle mit ±9 bereits maximal ungewiss. Besser gibt man also an, dass die nächst höhere Stelle um höchstens ±1 falsch sein kann: Das Ergebnis ist maximal zentimetergenau.

Oder anders ausgedrückt: Die endende Null auf der Einerstelle von 110 ist in diesem Fall signifikant. Um das deutlich zu machen, ohne die Fehlergrenzen mitzuschreiben, schreibt man besser 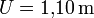$U = 1{,}10\,\mathrm{m}$, weil die ausdrückliche Angabe der Nachkommastelle zeigt, dass sie in dieser Rechnung als signifikant ermittelt wurde. 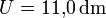$U = 11{,}0\,\mathrm{dm}$ hätte denselben Zweck. 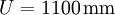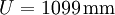Nicht geschrieben werden darf $U = 1100\,\mathrm{mm}$ oder $U = 1099\,\mathrm{mm}$, da die endende Null oder endende Neun aufgrund der Fehlergrenze keine signifikante Stelle ist.

Selbst ein exakteres π hätte nur ein Ergebnis von 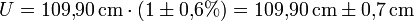$U = 109{,}90\,\mathrm{cm} \cdot (1 \pm 0{,}6 %) = 109{,}90\,\mathrm{cm} \pm 0{,}7\,\mathrm{cm}$ erbracht, die Signifikanz des Ergebnisses wäre dieselbe.

Dass in diesem Beispiel das Ergebnis nur zentimetergenau ist, obwohl die ursprüngliche Messung millimetergenau ausgeführt wurde, zeigt die Bedeutung der Stellensignifikanz für messtechnische Probleme: Weil das Ergebnis um grob eine Zehnerpotenz größer ist als die Angabe, und der Fall hier ungünstig liegt, verschiebt sich auch die Genauigkeit um eine Zeherpotenz von Millimeter auf Zentimeter. Die Größenordnung der Genauigkeit bleibt während der multiplikativen Rechnung nur relativ zum jeweiligen Wert konstant, die millimetergenaue Messung garantiert kein millimetergenaues Ergebnis. In komplizierteren Rechnungen lässt sich die Genauigkeit über die Anzahl signifikanter Stellen nicht mehr abschätzen, aber nur eine korrekte Fehlerfortpflanzungsrechnung garantiert die Verlässlichkeit eines Ergebnisses. Die nachträglich ermittelte Stellensignifikanz repräsentiert dann das Ergebnis der Fehleranalyse.

Weblinks

• Tipps zur Angabe von signifikanten Stellen bei Hausaufgaben
• Lösung mit MS Excel