- Zinseszinsformel
-
Der Zinseszins ist der Zins, der für bereits gutgeschriebene Zinsen eines früheren Berechnungszeitraumes gezahlt wird.
Das Verlangen nach Zinseszins wird als Anatozismus (v. griech.: anatokismós „Nehmen von Zinseszins“, aus aná „auf“ und tókos „Zins“) bezeichnet. Mit der Berechnung des Zinseszinses in Abhängigkeit vom Zinssatz sowie der Höhe und Dauer einer Kapitalanlage beschäftigt sich die Zinseszinsrechnung, ein Teilgebiet der Finanzmathematik.
Inhaltsverzeichnis
Zinseszinsrechnung
Die Zinseszinsrechnung beantwortet die Frage, auf welches Endkapital Kn ein anfängliches Kapital K0 nach insgesamt n Zeiträumen (kann auch ein Teilwert sein, s. Aufzinsung, Aufzinsfaktor) angewachsen ist, wenn in jedem dieser Zeiträume mit dem festen Zinssatz von p Prozent verzinseszinst wird.
- Zinseszinsformel:
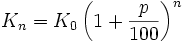
mit Kn = Endkapital; K0 = Anfangskapital; p = Zinssatz; n = Anzahl der geltenden Zeiträume/Jahre
Die Formel leitet sich aus folgendem Zusammenhang her: Ein Sparer tätigt eine einmalige Kapitalanlage auf einem Konto eines Kreditinstituts in Höhe eines anfänglichen Kapitals. Dieses Kapital wird während einer bestimmten Anlagedauer mit Zinseszins verzinst. Die Anlagedauer bestehe aus mehreren gleich langen Zeiträumen, die mit Hilfe der Natürlichen Zahlen fortlaufend durchgezählt werden. Man sagt auch, die Zeiträume werden mit dem Index i fortlaufend von i = 1 bis i = n durchnummeriert. Damit kann man die Anlagedauer als Summe aller n Zeiträume formulieren:
Zu Beginn des ersten Zeitraums (i = 1) liegt auf dem Konto des Sparers das anfängliche Kapital, das durch den Buchstaben K mit angehängtem Indexwert i = 0 dargestellt wird:
- Anfangskapital zu Beginn von Zeitraum1:K0
Wichtig sind die beiden verwendeten Indexwerte. Der erste Zeitraum erhält den Indexwert i = 1, während das Anfangskapital mit i = 0 nummeriert wird.
Der Sparer hat sich entschieden, für die Anlagedauer nicht auf sein Kapital zuzugreifen. Dafür „belohnt“ ihn das Kreditinstitut mit einer Gutschrift von Zinsen. Übliche Praxis ist nun, dass wiederholt jeweils am Ende von jedem der n Zeiträume innerhalb der Anlagedauer jeweils Zinsen gutgeschrieben werden.
Es wird also z. B. für den ersten Zeitraum der Zinswert Z1 vergütet:
Die konkrete Höhe des Zinswertes Z1 im ersten Zeitraum bestimmt sich wie folgt: Das Kreditinstitut drückt die „Belohnung“ des Sparers für die Überlassung des Kapitals in prozentualer Form aus, also z. B. „sechs Prozent“ (6 % = 6/100). Die reine Zahl, die vor dem Prozentzeichen steht, wird Zinssatz p genannt. Der am Ende des ersten Zeitraums gutgeschriebene Zinswert Z1 verhält sich zum anfänglichen Kapitalwert K0 genau so, wie sich der Zinssatz p zum Wert 100 verhält. Dieser Zusammenhang stellt eine Verhältnisgleichung dar.
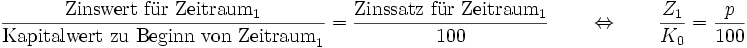 .
.
Diese Verhältnisgleichung erscheint viel theoretischer als das, was sie im praktischen Einsatz tatsächlich leistet. Sie besagt ganz einfach, dass ein z. B. mit sechs Prozent verzinstes Anfangskapital von 1.000 Euro im ersten Zeitraum einen Zinswert von genau 60 Euro „erwirtschaften“ muss, damit die gesuchten Verhältnisse stimmen:
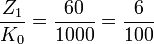 .
.
Diese Festlegung für das Verhältnis zwischen Zinswert und Kapitalwert im ersten Zeitraum lässt sich so verallgemeinern, dass für jedes Verhältnis von Zinswert Zi zu Kapitalwert K(i − 1) in jedem i-ten Zeitraum die Verhältnisgleichung gilt:
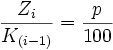 .
.
Nach Umstellung erhält man für den Zinswert Zi die Formel
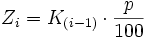 .
.
Für positive Zinssätze p > 0 gilt stets
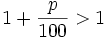 ,
,
weshalb dieser Term Aufzinsfaktor genannt wird. Bis hierhin wird deutlich, was mit „Verzinsung für einen Zeitraum“ gemeint ist.
Zur Betrachtung des Zinseszinses muss erneut berücksichtigt werden, dass der Sparer für das „zur Verfügung stellen“ des anfänglichen Kapitals K0 nach Maßgabe der obigen Zinswert-Formel „belohnt“ wird. Seinem Konto wird am Ende des ersten Zeitraums also folgender Zinswert Z1 gutgeschrieben:
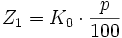 .
.
Somit wächst das anfängliche Kapital K0 bis zum Ende des ersten Zeitraums genau um diesen Zinswert Z1. Beide zusammen bilden also den neuen Kontostand. Diese Summe nennt man auch das (vorläufige) Endkapital K1, das folgerichtig mit dem Indexwert i = 1 versehen wird:
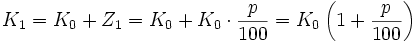 .
.
Dieses (vorläufige) Endkapital K1 ist nun zugleich das Anfangskapital für den zweiten Zeitraum (i = 2). Es „erwirtschaftet“ darin den Zinswert Z2, der erneut hinzuaddiert wird:
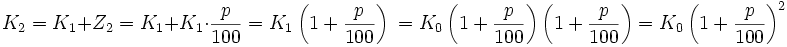 .
.
Damit wirkt bereits während des zweiten Zeitraums der Zinseszins-Effekt: Das Anfangskapital K0 im ersten Zeitraum wächst mit dem Aufzinsungsfaktor 1 + p/100 auf das (vorläufige) Endkapital K1. Auf die gleiche Weise steigt das Kapital K1 im zweiten Zeitraum mit demselben Aufzinsungsfaktor auf das (vorläufige) Endkapital K2. Über beide Zeiträume hinweg betrachtet ist das anfängliche Kapital K0 jedoch überproportional, nämlich mit dem Quadrat des Aufzinsungsfaktors, auf das (vorläufige) Endkapital K2 angewachsen.
Verallgemeinert bedeutet dies, dass sich am Ende der Anlagedauer, also nach insgesamt n Zinszeiträumen, schließlich das Endkapital Kn durch n-maliges Multiplizieren des Anfangskapitals K0 mit dem Aufzinsungsfaktor
ergibt.
Beispiel
Ein Betrag von 1000 Euro wird 10 Jahre lang zu einem jährlichen Zinssatz von fünf Prozent fest angelegt. Am Ende des ersten Jahres beträgt der Zins 1.000 € * 0,05 = 50 €. Für das zweite Jahr beträgt der Zins (1.000 € + 50 €) * 0,05 = 50 € + 2,50 €. Der Zinseszins-Effekt erwirtschaftet also einen Mehrertrag von 2,50 Euro im Vergleich zu einer Verzinsung ohne Zinseszins. Nach 10 Jahren ist das Anfangskapital durch Zinseszins angewachsen auf das Endkapital
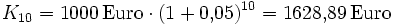 .
.
Aus den Zinseszins-Formeln kann man auch ableiten, wann sich ein Investment (Anlage eines Betrages zu einem Zinssatz) verdoppelt hat: 72er-Regel.
Exponentielles Wachstum
Ein weiteres einfaches Zinseszinsbeispiel soll die Problematik des mit dem Zinseszins verbundenen exponentiellen Wachstums verdeutlichen. Angenommen, im Jahr 1 unserer Zeitrechnung wird ein kleines Edelmetallkügelchen von 1 mm Durchmesser mit nur 3,55 % tatsächlich erzielbaren Zinsen, also einem Aufzinsungsfaktor von 1,0355, bei jährlicher Verzinsung in einer über die Laufzeit fix verzinsten Sparform angelegt. Es erfolgen keinerlei weitere Zahlungen, die Wertsteigerung erfolgt lediglich durch den Zinsgewinn. Der Wert definiert sich durch das Volumen der Edelmetallkugel, welche der Vorstellung wegen aus Gold sein kann. Ein Stück Gold wird deswegen in diesem Beispiel verwendet, um unabhängig von konkreten Währungen und deren Werten zu sein.
Durch den Zinseszins ist dieses kleine Goldkügelchen aus dem Jahr 1 mit nur 1 mm Durchmesser im Jahr 2001 auf eine stattliche Goldkugel mit einem Durchmesser von rund 12.600 km angewachsen - eine Goldkugel, welche fast so groß wie die Erde ist. Dies zeigt die praktische Unmöglichkeit, die sich bei längeren Anlageformen ergibt.
Rechengang, wobei D1 der Durchmesser der Edelmetallkugel im Jahr 1, D2001 der gesuchte Durchmesser im Jahr 2001, q der Aufzinsungsfaktor und l die Laufzeit in Jahren ist:
Recht
Im deutschen Zivilrecht ordnet § 248 Abs. 1 BGB an, dass eine im Voraus getroffene Vereinbarung, wonach Zinsen wieder Zinsen tragen sollen, nichtig ist. Die Vorschrift bezweckt einen Schutz des Schuldners vor der Kumulation von Zinsen. Gemäß Absatz 2 dieser Vorschrift gilt eine Ausnahme für Sparkassen, Kreditanstalten und Inhaber von Bankgeschäften. Diese können wirksam die Zahlung von Zinseszinsen versprechen. Auch beim handelsrechtlichen Kontokorrent können gem. § 355 HGB Zinseszinsen vereinbart werden. In § 289 BGB ist für den gesetzlichen Anspruch auf Zinsen als Ersatz des Verzugsschadens geregelt, dass von Zinsen keine Verzugszinsen zu entrichten sind. In § 353 S.2 HGB ist dieses noch einmal klarstellend dargelegt.
Siehe auch
- Josephspfennig
- Rentenrechnung
- Sparkassenformel
- Zinsrechnung (in diesem Artikel finden sich auch weitere Formeln zur Zinseszinsrechnung)
Weblinks
- § 248 BGB
- § 289 BGB
- § 353 HGB
- § 355 HGB
- Javascript zur Lösung von Standardaufgaben zur Zinseszinsrechnung: Berechnung von Anfangskapital, Endkapital, Zeit, Rate, Zinssatz
- Onlinerechner zur Zinseszinsrechnung für regelmäßige Sparraten mit Dynamikoption
- Erklärungen für Schüler
- Tutorial zur Zinsrechnung mit Übungsbeispielen und Lösungen
Bitte beachte den Hinweis zu Rechtsthemen! - Zinseszinsformel:
Wikimedia Foundation.

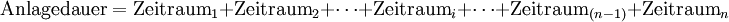
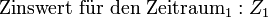
![D_{2001} = D_{1} \cdot \sqrt[3]{q^{l}} = 0{,}001\,\mathrm{m} \cdot \sqrt[3]{1{,}0355^{2000}} = 12.591.249{,}21\,\mathrm{m}](/pictures/dewiki/53/568d02163c0ab439d1b4b0a4757dbcc5.png)