Zweigstromanalyse

Als Netzwerkanalyse bezeichnet man in der Elektrotechnik die Vorgehensweise in einem Netzwerk (siehe Bild) aus den bekannten Werten der Schaltelemente sowie den vorgegebenen Quellgrößen alle Ströme und Spannungen zu berechnen. Von Hand und mit analytischen Methoden können mit realistischem Aufwand nur lineare Systeme untersucht werden. Die rechnergestützte Schaltungssimulation dagegen beruht vorwiegend auf iterativen Näherungsverfahren, benötigt sehr viele Rechenschritte, kann aber auch mit nichtlinearen Bauelementen umgehen.

Allgemein

In einem Netzwerk sind die Zusammenhänge zwischen allen auftretenden Strömen bzw. allen auftretenden Spannungen durch die nach dem deutschen Physiker Gustav Robert Kirchhoff benannten kirchhoffschen Regeln beschrieben. Der Zusammenhang zwischen Strom und Spannung ist durch das ohmsche Gesetz beschrieben, welche die Bauelementegleichung von Widerständen beschreibt. Voraussetzung sind reelle lineare Schaltelemente, d. h. kein kapazitiver oder induktiver Anteil und eine gerade Kennlinie im Gegensatz z. B. zur Diode.

Bei nicht reellen Widerständen wird die sog. komplexe Rechnung erforderlich. So lässt sich auch eine Analyse für Wechselspannung durchführen, wobei jede betrachtete Frequenz einzeln zu berechnen ist.

Damit eine Netzwerkanalyse möglich ist, werden in dem Netzwerk Knotenpunkte, Zweige und Maschen definiert. Mithilfe der kirchhoffschen Regeln können ihnen dann Gleichungen zugeordnet werden. Damit die mathematischen Gleichungssysteme zu einer eindeutigen Lösung führen, müssen die jeweiligen Gleichungen voneinander unabhängig sein.

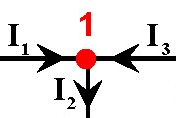
Ein Knotenpunkt ist dabei ein Punkt im Netzwerk, in dem eine Stromverzweigung auftritt. Ein Netzwerk beinhaltet dann k Knotenpunkte.

Insgesamt gibt es (k − 1) unabhängige Knotengleichungen, eine hiervon in dem gezeigten Beispiel ist

I₁ − I₂ + I₃ = 0.

Ein Zweig ist die Verbindung zweier Knoten durch Zweipolelemente.

Insgesamt gibt es z unabhängige Zweiggleichungen.

Im dargestellten Beispiel sind die Zweiggleichungen nach Ausnutzung der Bauelementgleichungen:

$U_{z1}=R_1 \cdot I_1 - U_{q1}$

$U_{z2}=R_2 \cdot I_2$

$U_{z3}=R3 \cdot I_3 + R4 \cdot I_3 - U_{q2}$

Als Baum bezeichnet man ein Gerüst aus Zweigen, welches alle Knoten verbindet, wobei kein Knoten zweimal berührt werden darf. Anschaulich ausgedrückt, die gebildete Struktur darf keine Möglichkeiten bieten, um im Kreis zu gehen. Für den Baum sind verschiedene Varianten möglich. Insgesamt sind bei einem vollständig vermaschten Netzwerk (jeder Knoten hat einen Zweig zu jedem anderen Knoten) k^{k − 2} Varianten denkbar. Im vorliegenden Beispiel ergeben sich drei unterschiedliche Bäume, da mehr als ein Zweig zwei Knoten miteinander verbindet.

Die einzelnen Zweige im Baum werden Baumzweige oder Äste genannt. Wegen des Aufbaus des Baumes gibt es a = k − 1 Äste.

Alle Zweige, die nicht zum Baum gehören, bezeichnet man als Sehnen oder auch Verbindungszweige. Dies entspricht der Zahl unabhängiger Maschengleichungen (z − (k − 1)), mit denen ein Gleichungssystem aufgestellt werden kann.

Somit existieren k - 1 unabhängige Knotengleichungen und m = z − (k − 1) unabhängige Maschengleichungen.

Eine Masche ist ein über Zweige geschlossener Umlauf. Für eine einfache Analyse sollte stets ein Umlauf über nur eine Sehne bzw. einen Verbindungszweig gewählt werden. Für den Fortlauf wird dieser Weg genutzt.

Der Umlaufsinn der m unabhängigen Maschen kann willkürlich festgelegt werden, ist jedoch relevant für spätere Berechnungen.

Im Beispiel sind die folgenden zwei Maschenumläufe gewählt.

$M1:\ -U_{q1} + U_1 + U_2 = 0$

$M2:\ U_{q2} - U_3 - U_4 - U_2 = 0$

Zweigstromanalyse

Zur Lösung mittels Zweigstromanalyse werden alle unabhängigen Knotengleichungen und die unabhängigen Maschengleichungen aufgestellt. Anschließend werden diese sortiert, indem man diese nach Strom/Widerstand auf der einen Seite der Gleichung und Spannungen auf der anderen Seite aufreiht. Als Ergebnis erhält man ein lineares Gleichungssystem.

Im gezeigten obigen Beispiel folgt hiermit dann in geordneter Reihenfolge (Knotengleichung 1, Maschengleichung 1 und Maschengleichung 2):

$I_1 - I_2 + I_3= 0,\quad\quad I_1 R_1+ I_2 R_2= U_{q1}, \quad\quad- I_2 R_2 - I_3 R_3 - I_3 R_4= -U_{q2}$

In Matrixschreibweise lautet nun das Gleichungssystem:

$\begin{pmatrix} 1 & -1 & 1 \\ R_1 & R_2 & 0 \\ 0 & - R_2 & - R_3 - R_4 \end{pmatrix} \cdot \begin{pmatrix} I_1 \\ I_2 \\ I_3 \end{pmatrix} = \begin{pmatrix} 0 \\ U_{q1} \\ -U_{q2} \end{pmatrix}$

Zur Lösung des linearen Gleichungssystems (Lineare Algebra) gibt es Standardmethoden die hierfür genutzt werden können. Kleinere Gleichungssysteme lassen sich analytisch „von Hand“ lösen, für umfangreichere Schaltkreise werden numerische Methoden (Computerprogramme) verwendet. (Ein Beispiel ist auf der Diskussionsseite)

Überlagerungsverfahren nach Helmholtz

Das Überlagerungsverfahren beruht auf dem Superpositionsprinzip bei linearen Systemen.

Vorgehen

• Bis auf eine Quelle werden alle anderen entfernt. Spannungsquellen werden durch Kurzschlüsse ersetzt bzw. Stromquellen als Unterbrechung gesehen. Die Innenwiderstände der Quellen verbleiben jedoch in der Schaltung.
• Die gesuchten Teilströme mit der verbliebenen Quelle berechnen.
• Das Vorgehen für jede andere Quelle wiederholen.
• Zum Schluss die vorzeichenrichtige Addition der errechneten Teilströme für die betrachteten Zweige durchführen.

Ergebnis

Der gesuchte Teilstrom wurde ermittelt.

Maschenstromverfahren

Mit zunehmender Komplexität steigt der Aufwand zur Berechnung des Netzwerks mit der Zweigstromanalyse. Eine Reduzierung des Rechenaufwands ergibt sich durch das Maschenstromverfahren.

Wien-Brücke

In das Baum-Diagramm eingezeichnete Maschen

Vorgehen (Kurzform)

1. Netzwerk vereinfachen
2. Baum wählen, ideale Stromquellen als Sehne
3. Nicht Ideale Stromquellen in eine äquivalente Spannungsquelle umwandeln
4. Maschen festlegen
5. Matrix aufstellen:

   $\begin{pmatrix} r_{11} & \dots & r_{1n} \\ \vdots & \ddots & \vdots \\ r_{n1} & \dots & r_{nn} \end{pmatrix} \cdot \begin{pmatrix} i_{M1} \\ \vdots \\ i_{Mn} \end{pmatrix} = \begin{pmatrix} u_{qM1} \\ \vdots \\ u_{qMn} \end{pmatrix}$

   $r_{ii} = \sum R\ in\ M_i$

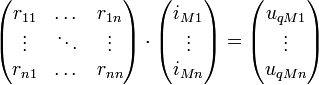
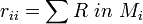
   $r_{ij} = r_{ji} = \sum [R\ in\ M_i\ und\ M_j \cdot Umlaufsinn(M_i,M_j)]$

   $u_{qMi} = \sum [U_q\ in\ M_i \cdot -1 \cdot Pfeil(U_q,M_i)]$

   Sonderfall ideale Stromquellen (I_q)

   $u_{qMi} = \sum [U_q\ in\ M_i \cdot -1 \cdot Pfeil(U_q,M_i)] - I_q \cdot \sum [R\ in\ M_i\ und\ M_{Iq} \cdot Umlaufsinn(M_i,M_{Iq})]$

6. Gleichungssystem lösen
7. Zweigströme berechnen anhand der Summe der Maschenströme

   I₁ = I_M1 + I_M2 − I_M3

Knotenpotentialverfahren

Wie beim Maschenstromverfahren ergibt sich beim Knotenpotentialverfahren ein reduziertes lineares Gleichungssystem.

Vorgehen (Kurzform)

1. Spannungsquellen in äquivalente Stromquelle umwandeln
2. Bezugsknotenpotential ("Masse") wählen, ideale Spannungsquellen an Bezugspotential angeschlossen (ansonsten mit dieser Anleitung nicht lösbar)
3. Restliche Knoten durchnummerieren
4. Matrix aufstellen, Knoten mit idealer Spannungsquelle weglassen

   $\begin{pmatrix} g_{11} & \dots & g_{1n} \\ \vdots & \ddots & \vdots \\ g_{n1} & \dots & g_{nn} \end{pmatrix} \cdot \begin{pmatrix} u_{10} \\ \vdots \\ u_{n0} \end{pmatrix} = \begin{pmatrix} i_{q1} \\ \vdots \\ i_{qn} \end{pmatrix}$

   $g_{ii} = \sum G\ mit\ Knoten\ i\ verbunden$

   $g_{ij} = g_{ji} = -1 \cdot \sum G\ zwischen\ den\ Knoten\ i\ und\ j\ (Koppelleitwerte)$

   $i_{qi} = \sum I_q\ an\ Knoten{,}\ I_q\ vom\ Knoten\ weg\ flie \beta end\ sind\ negativ$

5. Bei mit idealer Spannungsquelle gekoppelter Knoten, Spannungsquelle mit Koppelleitwert multiplizieren und zum Stromvektor addieren, wenn der Spannungspfeil zum Bezugsknotenpotential hin zeigt, andernfalls abziehen.
6. Gleichungssystem lösen.
7. Zweigspannung U_ij = u_i0-u_j0 aus den Knotenpotentialen ermitteln und daraus den Zweigstrom erreichen.

Literatur

• Singhal, K. Vlach, J.: Computer Methods for Circuit Analysis and Design. Verlag Springer US, ISBN 978-0-442-01194-9, 2. Aufl. 1993
• Führer, Heidemann, Nerreter – Grundgebiete der Elektrotechnik, Band 1: Stationäre Vorgänge, Carl Hanser Verlag München 1986, ISBN 3-446-13677-0
• Elschner, H., Moeschwitzer, A., Reibiger, A.: Rechnergestuetzte Analyse in der Elektronik. Reihe Informationselektronik. Verlag Technik Berlin, 1977
• Nagel, L.W.: Spice 2 - A Computer Programm to Simulate Semiconductor Circuits. University of Cal., Berkeley, CA, USA, Erl-Memorandum, Nr. Erl-M520, May 1975
• Nagel, L. W., Rohrer, R. A.: Computer Analysis of Nonlinear Circuits, Excluding Radiation. IEEE Journal of Solid State Circuits SC-6: 166–182, Aug. 1971

Siehe auch

• Schaltungssimulation, rechnergestütze Netzwerkanalyse
• Netzwerk (Elektrotechnik)
• Norton-Theorem, Ersatzstromquelle
• Thévenin-Theorem, Ersatzspannungsquelle
• Netzwerkanalysator SPICE