Bravaisgitter

Die Bravais-Gitter (nach Auguste Bravais) oder auch Raumgitter stellen die Menge aller im Raum möglichen Einheitszellen der Kristalle dar, die folgende Eigenschaften besitzen:

1. Die Einheitszelle ist die einfachste sich wiederholende Einheit in einem Kristall.
2. Gegenüberstehende Flächen einer Einheitszelle sind parallel.
3. Der Rand der Einheitszelle verbindet äquivalente Stellen.

Ein Bravais-Gitter besteht nur aus einer Teilchensorte. So ergibt sich z. B. das NaCl-Gitter durch Translation je eines kubisch-flächenzentrierten Gitters aus Na-Kationen und Cl-Anionen. Nach dieser Definition existieren 14 verschiedene Bravais-Gitter.

Verwendung

Der eigentlich rein mathematische Begriff des Bravais-Gitters findet oft Verwendung in den Naturwissenschaften, wie etwa der Kristallographie, Mineralogie, Materialwissenschaft, Festkörperchemie oder der Festkörperphysik, da sich so die Anordnung der Atome innerhalb eines Kristalls systematisch beschreiben lässt. Hierbei ist jedoch nicht notwendigerweise jeder Gitterpunkt durch ein Atom repräsentiert: Das Bravais-Gitter liefert ausschließlich das mathematische Gerüst, das in einer Kristallstruktur durch Atome (die Basis) aufgefüllt wird. Dieser Zusammenhang wird in der Kristallographie als fundamentales Prinzip verstanden: Kristall = Gitter + Basis.

Eine besondere Bedeutung hat es bei der Strukturaufklärung von Kristallen. Anhand der Metrik der Reflexe im reziproken Raum und deren systematischer integraler Auslöschung kann das Bravais-Gitter des Kristalls bestimmt werden.

Klassifikation

Die Bravais-Gitter werden anhand ihrer Punktgruppe den sieben Kristallsystemen zugeordnet. Entspricht die reduzierte Zelle des Bravais-Gitters dem Koordinatensystem des Kristallsystems, spricht man von einem primitiven Gitter.

Die weitere Differenzierung der sieben Kristallsysteme zu den 14 Bravais-Gittern erfolgt durch Anordnung weiterer Gitterpunkte, entweder in der Raummitte (raumzentriert oder innenzentriert), auf den Mittelpunkten aller Begrenzungsflächen (flächenzentriert) oder auf den Mittelpunkten der zwei Basisflächen (basiszentriert) der Elementarzelle.

Ein Gitter zusammen mit einer Basis, die aus einem Atom oder auch einer Atomgruppe bestehen kann, stellt eine Kristallstruktur dar.

Im Folgenden sind die Bravais-Gitter nach den Kristallsystemen, mit abnehmender Symmetrie, geordnet.

Rechtwinklige (orthogonale) Achsensysteme

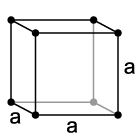
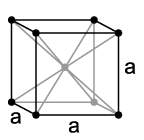
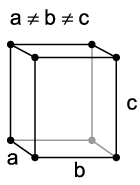
Kubisches Kristallsystem

• höchste Symmetrie
• drei gleichlange Achsen im 90°-Winkel

Kubisch-Primitives Gitter (sc)	Kubisch-Raumzentriertes Gitter (bcc)	Kubisch-Flächenzentriertes Gitter (fcc)

Tetragonales Kristallsystem

• zwei gleichlange Achsen, drei 90°-Winkel

Tetragonal-Primitives Gitter	Tetragonal-Raumzentriertes Gitter

Rhombisches Kristallsystem

• auch orthorhombisches Kristallsystem
• drei 90°-Winkel, keine gleichlangen Achsen

Rhombisch-Primitives Gitter	Rhombisch-Basiszentriertes Gitter	Rhombisch-Raumzentriertes Gitter	Rhombisch-Flächenzentriertes Gitter

Schiefwinklige Achsensysteme

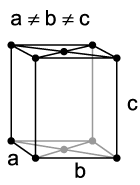
Hexagonales Kristallsystem

• zwei gleichlange Achsen in einer Ebene im 120°-Winkel, die dritte Achse senkrecht dazu

Hexagonal-Primitives Gitter

Trigonales Kristallsystem

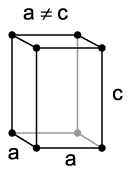
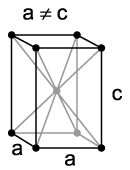
• Trigonale Kristallstrukturen können ebenfalls im hexagonalen Gitter beschrieben werden:

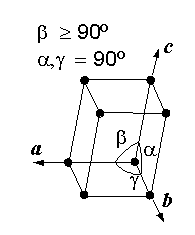
- hexagonale Aufstellung: a = b ≠ c , α = β = 90° , γ = 120° (siehe Abbildung oben)

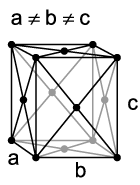
• Als Spezialfall kann eine rhomboedrische Zentrierung auftreten:

- drei gleichlange Achsen, drei gleiche Winkel ungleich 90° (siehe Abbildung unten)

- nicht mit dem orthorhombischen Kristallsystem zu verwechseln

Rhomboedrisches Gitter

Monoklines Kristallsystem

• zwei 90°-Winkel, keine gleichlangen Achsen

Monoklin-Primitives Gitter	Monoklin-Basiszentriertes Gitter

Triklines Kristallsystem

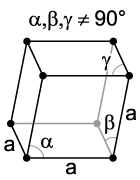
• geringste Symmetrie aller Gitter
• keine gleichen Winkel, keine gleichlangen Achsen

Triklin-Primitives Gitter

Bravais-Gitter in nicht-dreidimensionalen Räumen

Im Zweidimensionalen gibt es fünf Bravais-Gitter^[1]: das schiefwinklige Gitter sowie vier spezielle Typen: das quadratische, das rechteckige, das hexagonale sowie das zentriert-rechteckige Gitter. Die Oberfläche aller dreidimensionalen Gittertypen besteht aus diesen zweidimensionalen Gittertypen. Sie haben daher in der Oberflächenphysik sowie der Nanotechnologie eine große Bedeutung.

Die fünf zweidimensionalen Bravais-Gitter: 1 schiefwinklig, 2 rechtwinklig, 3 rechtwinklig zentriert, 4 hexagonal, und 5 quadratisch

Im Vierdimensionalen gibt es 52 Bravais-Gitter, von denen 21 primitiv sind.^[2] .

Einzelnachweise

1. ↑ Martin Henzler, Wolfgang Göpel: Oberflächenphysik des Festkörpers. Teubner, Stuttgart 1994, ISBN 3-519-13047-5. 
2. ↑ Mackay AL and Pawley GS: Bravais Lattices in Four-dimensional Space. In: Acta. cryst.. 16, 1963, S. 11–19. doi:10.1107/S0365110X63000037