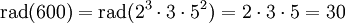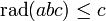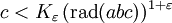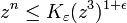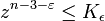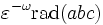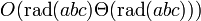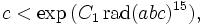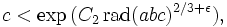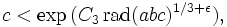Abc-Vermutung

Die abc-Vermutung ist eine 1985 von Joseph Oesterlé und David Masser aufgestellte mathematische Vermutung. Dabei geht es um eine Eigenschaft von Tripeln von untereinander teilerfremden natürlichen Zahlen, bei denen die dritte die Summe der beiden anderen ist. Die Vermutung ist bisher weder bewiesen noch widerlegt. Es sind allerdings bereits eine Anzahl weitreichender zahlentheoretischer Aussagen bekannt, die aus der Gültigkeit der abc-Vermutung folgen würden.

Formulierung

Ein Tripel (a,b,c) heißt abc-Tripel, wenn a und b teilerfremde positive ganze Zahlen sind und c = a + b ihre Summe ist. Aufgrund elementarer Eigenschaften der Teilbarkeitsbeziehung ist c sowohl zu a als auch zu b teilerfremd.

Das Radikal 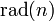$\operatorname{rad}(n)$ einer positiven ganzen Zahl n ist das Produkt der unterschiedlichen Primfaktoren von n. Primfaktoren, die in der Primfaktorzerlegung von n mehrfach vorkommen, werden bei der Berechnung von 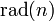$\operatorname{rad}(n)$ nur einmal berücksichtigt. Beispielsweise ist

$\operatorname{rad}(600) = \operatorname{rad}(2^3 \cdot 3 \cdot 5^2) = 2 \cdot 3 \cdot 5 = 30$

Trifft für ein abc-Tripel die Ungleichung

$\operatorname{rad}(abc) \le c$

zu, wird es als abc-Treffer bezeichnet. Ein Beispiel ist das von Eric Reyssat gefundene Tripel (2,6436341,6436343) mit 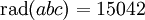$\operatorname{rad}(abc) = 15042$. abc-Treffer sind selten. Unter den 15 Millionen abc-Tripeln mit c < 10.000 gibt es nur 120 abc-Treffer und unter den 380 Millionen abc-Tripeln mit c < 50.000 gibt es 276.

Obwohl also 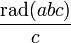$\frac {\operatorname{rad}(abc)}{c}$ meist größer als 1 ist, bewies Masser, dass das Verhältnis beliebig klein werden kann.^[1] Für Exponenten 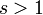$\,s &amp;gt; 1$ (auch wenn sie 1 beliebig nahe kommen), formulierte er allerdings mit Oesterlé die abc-Vermutung, dass 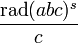$\frac {\operatorname{rad}(abc)^s}{c}$ eine positive untere Schranke besitzt.

Genauer formuliert lautet die abc-Vermutung:

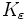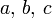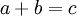Für jedes reelle $\varepsilon &amp;gt; 0$ existiert eine Konstante $K_\varepsilon$, sodass für alle Tripel teilerfremder positiver ganzer Zahlen $a,\, b,\, c$ mit $\,a+b=c$ die folgende Ungleichung gilt:

$c &amp;lt; K_\varepsilon \, (\mathrm{rad}(abc))^{1 + \varepsilon}$

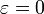Die Vermutung wird für $\varepsilon &amp;gt; 0$ formuliert, da sie für $\varepsilon = 0$ wie erwähnt nachweislich falsch ist.

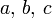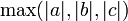Man kann die Vermutung auch für beliebige positive oder negative ganze Zahlen $a,\,b,\,c$ formulieren und hat dann nur auf der linken Seite der Ungleichung $\,c$ durch $\, \operatorname{max} (|a|, |b|, |c|)$ zu ersetzen.

Folgerungen aus der abc-Vermutung

Die Vermutung konnte bisher zwar nicht bewiesen werden, zieht allerdings eine Menge interessanter Konsequenzen nach sich. Viele gelöste und ungelöste diophantische Probleme lassen sich aus dieser Vermutung folgern. Insbesondere der sehr komplexe und komplizierte Beweis des Großen fermatschen Satzes würde sich auf eine Seite reduzieren.

• Satz von Thue-Siegel-Roth, wie Machiel van Frankenhuysen 1999 zeigte.
• Großer fermatscher Satz
• Vermutung von Mordell (von Gerd Faltings bewiesen), wie Noam Elkies 1991 zeigte.
• Erdős-Woods-Vermutung
• die Existenz von endlich vielen Nicht-Wieferich-Primzahlen. Allgemeiner zeigte Joseph Silverman 1988, dass aus der abc-Vermutung folgt, dass es unendliche viele Primzahlen p gibt, für die a^{p − 1} − 1 nicht durch p² teilbar ist.
• die schwache Form der Hall-Vermutung, die eine asymptotische untere Schranke zwischen dem Betrag der Differenz von Kuben und Quadraten liefert.
• die Vermutung von Lucien Szpiro (einer Ungleichung zwischen Führer und Diskriminante elliptischer Kurven über den rationalen Zahlen). Diese Vermutung ist sogar äquivalent zur abc Vermutung.^[2]

Als Beispiel wird die abc-Vermutung auf den großen Fermatschen Satz angewandt, dass

xⁿ + yⁿ = zⁿ

keine Lösung in positiven ganzen Zahlen x,y,z (die als relativ prim angenommen werden) hat für n > 2

Setzt man in der Ungleichung der abc-Vermutung 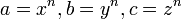$\,a=x^n, b = y^n, c=z^n$ ein und benutzt

$\operatorname{rad}(x^n y^n z^n) = \operatorname{rad}(xyz) \le xyz &amp;lt; z^3$,

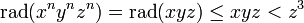lautet die Ungleichung dann:

$z^n \le K_{\varepsilon} (z^3)^{1+\epsilon}$

Wählt man die Ungleichung für 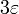$3 \varepsilon$, hat man für 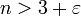$n &amp;gt; 3 + \varepsilon$ eine obere Schranke für z:

$z^{n-3-\varepsilon} \le K_{\epsilon}$

Das heißt, die Fermatgleichung kann nur endlich viele Lösungen haben, und ab einem bestimmten Wert des Exponenten n, der nur von 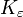$K_{\varepsilon}$ abhängt, das durch die abc-Vermutung gegeben wäre, überhaupt keine Lösung mehr, da z > 1. Man braucht nur alle Fälle n bis zu dieser Grenze mit anderen Methoden zu überprüfen, um die Fermatvermutung zu beweisen (für eine große Zahl von Exponenten n war das Zutreffen der Vermutung schon vor dem Beweis von Andrew Wiles bekannt).

Spezielle Form der abc-Vermutung

Eine etwas speziellere Formulierung der Vermutung postulierte Alan Baker 1996,^[3] indem er rad(abc) durch

$\varepsilon^{-\omega} \mathrm{rad}(abc)$

ersetzte, wobei ω die Anzahl der unterschiedlichen Primfaktoren von a, b und c ist. Eine verwandte Vermutung von Andrew Granville setzt fest, dass die rechte Seite des Terms auch durch

$\, O(\mathrm{rad}(abc) \Theta(\mathrm{rad}(abc)))$

ersetzt werden kann, wobei Θ(n) die Anzahl der ganzzahligen Zahlen bis n ist, die nur durch Primzahlen teilbar sind, die n teilen.

Wird auf der linken Seite der Ungleichung der abc Vermutung statt 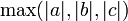$\, \operatorname{max}(|a|, |b|, |c|)$ der Wert 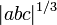$\, |abc|^{1/3}$ eingesetzt, spricht man auch von schwacher abc-Vermutung.

abc-Vermutung für Polynome

W. Stothers und Richard Mason (1983) bewiesen^[4] unabhängig folgenden, bis dato unbekannten Satz für Polynome:

Seien 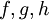$\,f, g, h$ teilerfremde, nicht-konstante Polynome mit 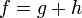$\,f = g + h$. Dann ist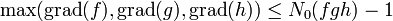

$\operatorname{max}(\operatorname{grad}(f), \operatorname{grad}(g), \operatorname{grad}(h)) \le N_0 (fgh) - 1$

wobei 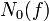$\,N_0 (f)$ die Anzahl der verschiedenen Nullstellen von f ist. Das ist gewissermaßen das „Funktionenkörper“-Analogon der abc-Vermutung. Sein Beweis ist relativ einfach (siehe z. B. Serge Lang, Elemente der Mathematik, Bd.48, 1993, S. 91 f) und wie auch im Fall der abc-Vermutung folgt daraus z. B. der fermatsche Satz für Polynome. Die Übersetzung vom Polynom-Fall in die abc-Vermutung für ganze Zahlen erfolgt dadurch, dass man 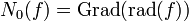$\,N_0 (f) = \operatorname{Grad}(\operatorname{rad} (f) )$ setzt, wobei 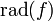$\,\operatorname{rad}(f)$ das Produkt der „Primfaktoren“ (x − a) von f ist, erstreckt über alle Wurzeln a von f, und den Grad durch sein Analogon den Logarithmus ersetzt (da $\operatorname{grad}(f g) = \operatorname{grad}(f) + \operatorname{grad}(g))$.

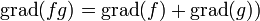Diese „Modell“-Version der abc-Vermutung war allerdings nicht die unmittelbare Motivation für die Vermutung durch Oesterlé und Masser. Das Motiv für die Vermutung ergab sich auch nicht aus numerischen Rechnungen, sondern vielmehr aus tiefliegenden Untersuchungen über elliptische Kurven in der Zahlentheorie,^[5] die sich teilweise in der verwandten Vermutung von Lucien Szpiro widerspiegeln (siehe oben).

Teilergebnisse

Bisher wurden folgende Ungleichungen für c und rad (a,b,c) bewiesen:

1986, C.L. Stewart und R. Tijdeman:

$c &amp;lt; \exp{(C_1\, \operatorname{rad}(abc)^{15}) },$

1991, C.L. Stewart und Kunrui Yu:

$c &amp;lt; \exp{ (C_2\, \operatorname{rad}(abc)^{2/3+\epsilon}) },$

1996, C.L. Stewart und Kunrui Yu:

$c &amp;lt; \exp{ (C_3\, \operatorname{rad}(abc)^{1/3+\epsilon}) },$

wobei C₁ eine festgelegte Konstante ist und C₂ sowie C₃ positive leicht berechenbare Konstanten in Abhängigkeit von ε.

Literatur

• D. W. Masser: Note on a conjecture of Szpiro. Astérisque Bd.184, 1990, S.19.
• C. L. Stewart, R. Tijdeman: On the Oesterlé-Masser Conjecture. Monatshefte für Mathematik 102, 251-257, 1986; online hier (pdf).
• Joseph Oesterlé: Nouvelles approches du «théorème» de Fermat. Séminaire Bourbaki Nr.694, 1987/8, die Vermutung ist dort zuerst formuliert.

Weblinks

• Abderrahmane Nitajs Webseite über die abc-Vermutung
• Ivars Peterson: The Amazing ABC Conjecture. 8. Dezember 1997 (englisch).
• Eric W. Weisstein: abc Conjecture auf MathWorld (englisch)
• Andrew Granville, Thomas J. Tucker: It's As Easy As abc. Notices AMS 2002, pdf-Datei.
• Projekt, das versucht, mit Hilfe von verteiltem Rechnen dieses Problem zu lösen
• Serge Lang: Die abc-Vermutung. In: Elemente der Mathematik, Band 48, 1993.
• Frits Beukers: Vortragsfolien (englisch)
• Masser und Oesterlé über den Ursprung der abc-Vermutung, holländischer Text mit Links auf Masser, Oesterlé

Verweise

1. ↑ Ein einfacher Beweis nach Wojtek Jastrzebowski und Dan Spielman findet sich bei Lang, Elemente der Mathematik, Bd.48, 1993, S.94. Ihr Gegenbeispiel zur abc-Vermutung mit ε = 0 ist 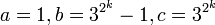$a = 1, b =3^{2^k}-1, c=3^{2^k}$. Man beweist durch Induktion, dass b durch 2^k teilbar ist. Das ergibt eine Ungleichung, die nicht für alle k erfüllt sein kann.
2. ↑ William Stein: Szpiro and ABC. (englisch)
3. ↑ Alan Baker: Log forms and the abc conjecture. In: Number Theory. Eger 1996, de Gruyter 1998.
4. ↑ Mason: Diophantine equations over function fields. Cambridge University Press 1984, W.W.Stothers: Polynomial identities and Hauptmoduln. Quarterly Journal Mathematics, Oxford, II. Ser., Bd. 32, 1981, 349-370. Auch Joseph Silverman bewies unabhängig den Satz, der auch PQR-Theorem oder Stothers-Mason-(Silverman)-Theorem genannt wird.
5. ↑ Oesterlé zur Motivation hinter ihrer Postulierung der abc-Vermutung