Caesar Shift

Schematische Darstellung einer Verschiebechiffre hier mit Schlüssel C, also Verschiebung um drei Buchstaben

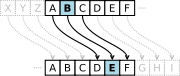
Die Verschiebechiffre (auch als Caesar-Verschlüsselung, Caesar-Verschiebung oder schlicht als „Einfacher Caesar“ bezeichnet) ist ein besonders simpler Sonderfall einer einfachen (das heißt monographischen) monoalphabetischen Substitution. Zum Zwecke der Verschlüsselung wird dabei jeder Buchstabe des lateinischen Standardalphabets um eine bestimmte Anzahl von Positionen zyklisch verschoben (rotiert). Die Anzahl bestimmt den Schlüssel, der für die gesamte Verschlüsselung unverändert bleibt. Es ist eine der einfachsten und unsichersten Formen einer Geheimschrift.

Geschichte

Der Name der Caesar-Verschlüsselung leitet sich vom römischen Feldherrn Gaius Julius Caesar ab, der diese Art der geheimen Kommunikation für seine militärische Korrespondenz verwendet hat. Dabei benutzte Caesar selbst häufig den Schlüssel C, also eine Verschiebung des Alphabets um drei Buchstaben. Der römische Kaiser Augustus soll eine Verschiebung der Buchstaben um nur eine Position vorgezogen haben (vielleicht passend zu seinem Namen, der mit A beginnt).

Der römische Schriftsteller Sueton beschreibt das Verfahren wie folgt:^[1]

„… si qua occultius perferenda erant, per notas scripsit, id est sic structo litterarum ordine, ut nullum verbum effici posset: quae si qui investigare et persequi velit, quartam elementorum litteram, id est D pro A et perinde reliquas commutet.“

„… wenn etwas Geheimes zu überbringen war, schrieb er in Zeichen, das heißt, er ordnete die Buchstaben so, dass kein Wort gelesen werden konnte: Um diese zu lesen, tauscht man den vierten Buchstaben, also D für A aus und ebenso mit den restlichen.“

Die Caesarchiffre wird als Teil komplexerer Verschlüsselungsverfahren – etwa der im Jahr 1508 von Trithemius zum ersten mal mit Hilfe seiner Tabula recta erläuterten polyalphabetischen Substitution oder auch der Vigenère-Chiffre – eingesetzt. Selbst heute noch ist sie in Gestalt des in der elektronischen Kommunikation verbreiteten ROT13-Systems zur Verschleierung von Nachrichten in Gebrauch.

Funktionsweise

Ordnet man den Buchstaben des Alphabets Zahlen zu, wie beispielsweise in der folgenden Tabelle, so lässt sich mithilfe eines „Schlüsselbuchstabens“ angeben, um wie viele Zeichen das Standardalphabet verschoben werden muss, um das Geheimalphabet zu erhalten.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

Beispielsweise entspricht der Schlüssel C einer zyklischen Verschiebung um drei Zeichen. Folglich wird beispielsweise der Buchstabe „r“ als „U“ verschlüsselt. Zur deutlichen Unterscheidung ist es üblich, Klarbuchstaben klein zu schreiben und Geheimbuchstaben groß. Somit ergibt sich folgende Zuordnung:

Klar:    a b c d e f g h i j k l m n o p q r s t u v w x y z
Geheim:  D E F G H I J K L M N O P Q R S T U V W X Y Z A B C

Da man sich das Geheimalphabet auch durch Rotation (zyklische Verschiebung) des Klaralphabets erzeugt denken kann, wird es auch als „rotiertes Alphabet“ bezeichnet. In diesem Spezialfall bei Schlüssel „C“ wäre es als ROT3 zu bezeichnen.

Aus dem Klartext „caesar“ wird bei Verschlüsselung mit dem Schlüssel C der Geheimtext „FDHVDU“.

Varianten

Es gibt verschiedene Varianten dieser Methode, wobei in das Alphabet noch Ziffern oder Sonderzeichen einbezogen werden können.

Ein wichtiger Sonderfall der „normalen“ Caesar-Verschlüsselung entsteht bei Verwendung des Schlüssels M, also einer Rotation um 13 Zeichen (ROT13). Da das (heutige) lateinische Alphabet aus 26 Buchstaben besteht, wird durch die zyklische Verschiebung um 13 Buchstaben, zunächst der Text verschlüsselt, und durch eine zweite Verschlüsselung mit demselben Schlüssel, eine Gesamtverschiebung um 26 Buchstaben erreicht und so der Originaltext zurückgewonnen. Dies ist ein besonders einfacher Fall einer involutorischen Verschlüsselung. Bei involutorischen Verfahren sind Verschlüsselung und Entschlüsselung identisch und eine zweifache Anwendung des Verfahrens liefert den ursprünglichen Klartext wieder zurück.

Eine weitere Variante der Verschiebechiffre besteht darin, statt des Standardalphabets ein revertiertes (umgekehrtes) Alphabet zu benutzen und dieses zu verschieben. Diese Methode wird oft knapp als „revertierter Caesar“ bezeichnet. Für beispielsweise den Schlüssel „C“, also wieder eine Verschiebung um drei Zeichen, erhält man dann das folgende Geheimalphabet:

Klar:    a b c d e f g h i j k l m n o p q r s t u v w x y z
Geheim:  C B A Z Y X W V U T S R Q P O N M L K J I H G F E D

In diesem Fall würde aus „caesar“ der Geheimtext „ACYKCL“ entstehen. Ein wichtiger Sonderfall des revertierter Caesars entsteht, wenn das Alphabet nicht verschoben wird. Hierbei wird das Standardalphabet auf das revertierte Standardalphabet abgebildet, also

Klar:    a b c d e f g h i j k l m n o p q r s t u v w x y z
Geheim:  Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

Dieser Spezialfall ist auch als eigenständige Methode einer Geheimschrift unter dem Namen Atbash bekannt.

Entzifferung

Häufigkeitsverteilung der Monogramme für Englisch als Beispiel für die ungleichförmige Verteilung der Buchstaben in einem Klartext und auch in einem Caesar-verschlüsselten Geheimtext

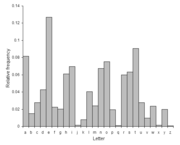
Wie alle monoalphabetischen Verschlüsselungsverfahren bietet auch die Verschiebechiffre keine hinreichende Sicherheit gegen unbefugte Entzifferung und kann sehr leicht „geknackt“ werden. Die in der natürlichen Sprache ungleiche Verteilung der Buchstaben wird durch diese Art der Verschlüsselung nicht verborgen, so dass eine Häufigkeitsanalyse das Wirken einer einfachen monoalphabetischen Substitution enthüllt. Noch einfacher nutzt der Angreifer die sehr kleine Anzahl der möglichen Schlüssel. Da die Größe des Schlüsselraums nur 25 beträgt, was einer „Schlüssellänge“ von nicht einmal 5 bit entspricht, liegt nach Ausprobieren spätestens nach dem 25. Versuch der Klartext vor. Eine erschöpfende Schlüsselsuche (Exhaustion) ist bei der Caesar-Verschlüsselung trivial realisierbar.

Literatur

• Friedrich L. Bauer: Entzifferte Geheimnisse, Methoden und Maximen der Kryptographie. Springer, Berlin 2000 (3. Aufl.), ISBN 3-540-67931-6
• Rudolf Kippenhahn: Verschlüsselte Botschaften. Die Geheimschrift des Julius Caesar - Geheimschriften im I. und II. Weltkrieg - Das Codebuch des Papstes - Enigma. 4. Aufl. Hamburg, 2006. ISBN 393-787-237-X.

Weblinks

• Tool zum automatisierten Knacken der Cäsarchiffre

Belege

1. ↑ De Vita Caesarum: Divus Julius LVI