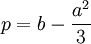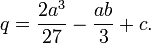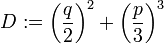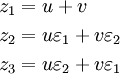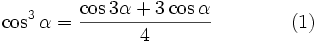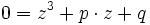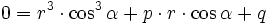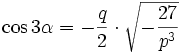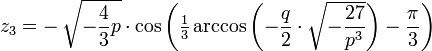Casus irreducibilis

Die cardanischen Formeln sind Formeln zur Lösung reduzierter kubischer Gleichungen (Gleichungen 3. Grades). Sie wurden, zusammen mit Lösungsformeln für quartische Gleichungen (Gleichungen 4. Grades), erstmals 1545 von dem Mathematiker Gerolamo Cardano in seinem Buch Ars magna veröffentlicht. Entdeckt wurde die Lösungsformel für kubische Gleichungen von Tartaglia; laut Cardano sogar noch früher durch Scipione del Ferro.

Die cardanischen Formeln waren eine wichtige Motivation für die Einführung der komplexen Zahlen, da man im Fall des casus irreducibilis durch das Ziehen einer Quadratwurzel aus einer negativen Zahl zu reellen Lösungen gelangen kann.

Die cardanischen Formeln besitzen heute für eine rein numerische Lösung kubischer Gleichungen kaum noch eine praktische Bedeutung, da sich die Lösungen bequemer durch das Newton-Verfahren mittels elektronischer Rechner bestimmen lassen. Sie sind dagegen für eine exakte Berechnung der Lösungen in Radikalen von erheblicher Bedeutung. Der Nachweis, dass es keine entsprechenden Formeln für Gleichungen fünften und höheren Grades geben kann, hat allerdings die Entwicklung der Algebra entscheidend beeinflusst (siehe Galoistheorie).

Reduzierung der allgemeinen Gleichung dritten Grades

Zusammenhang zwischen Vorzeichen der Diskriminante und der Anzahl der Nullstellen

Die allgemeine Gleichung dritten Grades

Ax³ + Bx² + Cx + D = 0

mit reellen Zahlen A,B,C,D und $A\ne0$ kann durch Division durch A zunächst in die Normalform

x³ + ax² + bx + c = 0

gebracht werden. Mit Hilfe der Substitution 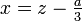$x = z-\tfrac{a}3$ wird in der Normalform das quadratische Glied beseitigt und man erhält die reduzierte Form:

z³ + pz + q = 0,

wobei

$p= b - \frac{a^2}3$

und

$q= \frac {2a^3}{27} - \frac{ab}3 + c.$

Die reduzierte Form wird nun mit Hilfe der Cardanischen Formel aufgelöst und anschließend durch Rücksubstitution 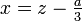$x=z-\tfrac{a}3$ die Lösungen der ursprünglichen Gleichung bestimmt.

Die Cardanische Formel zur Auflösung der reduzierten Form z³ + pz + q = 0

Im Unterschied zur Quadratischen Gleichung ist es bei der kubischen Gleichung erforderlich komplexe Zahlen zu betrachten, insbesondere auch dann, wenn alle drei Lösungen reell sind. Diese Tatsache hat im 16.Jh. zur Anerkennung der komplexen Zahlen geführt.

Die drei Lösungen ergeben sich durch z = u + v mit $u = \sqrt[3]{-\frac{q}2 + \sqrt{D}}$ und $v = \sqrt[3]{-\frac{q}2 - \sqrt{D}}$, wobei

$D:=\left(\frac{q}2\right)^2 + \left(\frac{p}3\right)^3$

die Diskriminante der reduzierten Form ist. Die beiden komplexen 3. Wurzeln u und v müssen dabei so gewählt werden, dass die Nebenbedingung $u\cdot v = -\frac{p}3$ erfüllt ist (dadurch gibt es statt 9 nur 3 Paare (u,v).

Die beiden anderen dritten Wurzeln ergeben sich dann jeweils durch Multiplikation mit den beiden primitiven dritten Einheitswurzeln 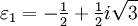$\varepsilon_1=-\tfrac12 + \tfrac12 i\sqrt3$ und $\varepsilon_2 = \varepsilon_1^2 = -\tfrac12 - \tfrac12 i\sqrt3$. Wegen der Nebenbedingung ergeben sich die drei Lösungen der reduzierten Form zu

$\begin{align} z_1 &= u + v\\ z_2 &= u\varepsilon_1 + v\varepsilon_2\\ z_3 &= u\varepsilon_2 + v\varepsilon_1 \end{align}$

Das Lösungsverhalten hängt entscheidend vom Vorzeichen der Diskriminante ab:

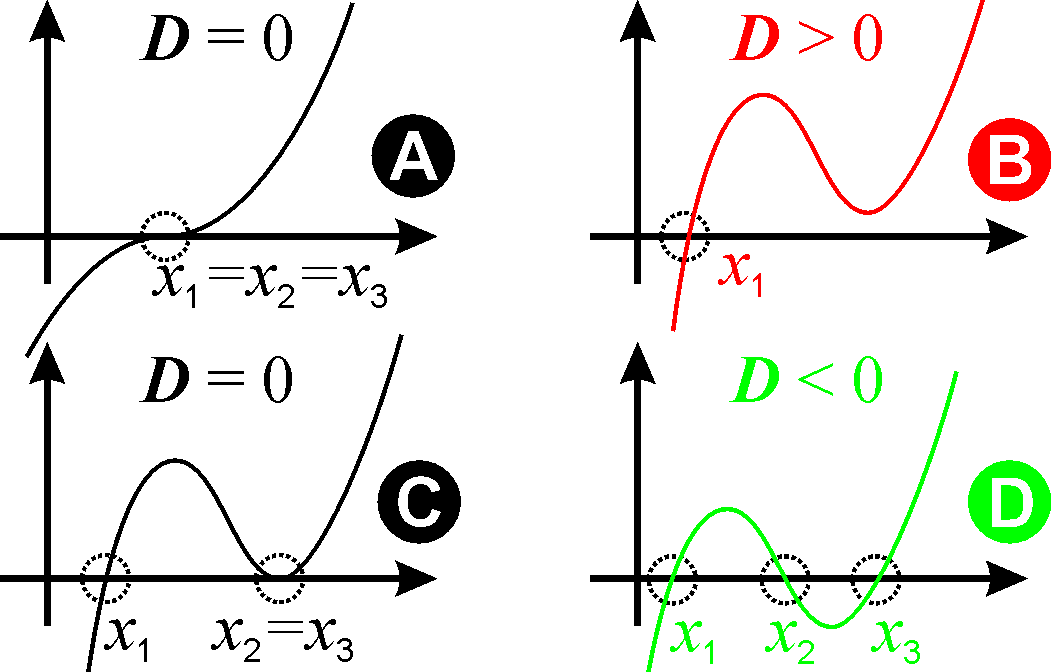
• D > 0: Es gibt genau eine reelle Lösung und zwei echt komplexe Lösungen (Grafik: Fall B).
• D = 0: Es gibt entweder eine doppelte reelle Lösung und eine einfache reelle Lösung (Fall C) oder eine dreifache reelle Lösung (Fall A).
• D < 0: Es gibt drei verschiedene reelle Lösungen (Fall D).

Im Fall D > 0 gibt es für den Verlauf des zugehörigen Graphen zwei Möglichkeiten: entweder (Fall B) oder streng monoton wachsend (nicht im Bild dargestellt).

D > 0

Man wählt für u und v jeweils die reellen Wurzeln. Es gibt genau eine reelle und zwei konjugiert komplexe Lösungen, die nach den obigen Formeln durch

$\begin{align} z_1&amp;amp;amp;=u + v\\ z_{2,3} &amp;amp;amp;= -\frac{u+v}2 \pm \frac{u-v}2\,\mathrm i \sqrt3 \end{align}$

gegeben sind.

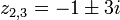Allerdings ist das Ausziehen der Kubikwurzeln nicht immer so einfach. Cardano führt als Beispiel an: z³ + 6z − 20 = 0. Hierbei wählen wir $u=\sqrt[3]{10 + \sqrt{108}} = 1+\sqrt3$ und $v=\sqrt[3]{10 - \sqrt{108}} = 1-\sqrt3$ reell. Somit ergibt sich z₁ = 2 und $z_{2,3}=-1\pm 3i$. Auf die Techniken zum Ausziehen von verschachtelten Wurzeln sei auf die Fachliteratur verwiesen.

D = 0

In diesem Fall wählt man u = v reell. Nach den obigen Formeln gibt es dann eine einfache reelle Lösung

$z_1 = 2u = \sqrt[3]{-4q} = \frac{3q}p$,

und eine doppelte reelle Lösung

$z_{2,3} = -u = \sqrt[3]{\frac{q}2} = -\frac{3q}{2p}$.

Ist p = q = 0, so ist z = 0 die einzige (dreifache) Lösung.

D < 0 (casus irreducibilis)

Man wählt u und v jeweils konjugiert komplex zueinander, so ergeben sich dann durch 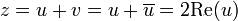$z=u+v = u+\overline{u} = 2\operatorname{Re}(u)$ drei verschiedene reelle Lösungen.

Bei der Bestimmung von u müssen jedoch dritte Wurzeln aus echt komplexen Zahlen (z.B. mit Hilfe des Satzes von de Moivre) berechnet werden. Deshalb wird dieser Fall casus irreducibilis genannt. Mithilfe der trigonometrischen Funktionen können die Lösungen jedoch auch reell berechnet werden: Nach den Additionstheoremen, gilt für alle α die Beziehung

$\cos^3\alpha=\frac{\cos 3\alpha+3\cos\alpha}4\qquad\qquad(1)$

Schreibt man

$0=z^3+p\cdot z+q$

mit Hilfe des Ansatzes $z=r\cdot\cos\alpha$ um, ergibt sich

$0=r^3\cdot\cos^3\alpha+p\cdot r\cdot\cos\alpha+q$

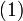Setzt man hierin $(1)\,$ ein, dann entsteht

$\begin{align} 0&amp;amp;amp;=r^3\cdot\frac{\cos 3\alpha+3\cos\alpha}4 + p\cdot r\cdot\cos\alpha+q \\ &amp;amp;amp;=\frac{r^3}4 \cos 3\alpha + \left(\frac34r^2 + p\right)\cdot r\cdot\cos\alpha+q \\ &amp;amp;amp;\,\stackrel{(2)}= \sqrt{-\frac{4}{27}\,p^3}\cdot\cos 3\alpha+q \end{align}$

Dabei wurde 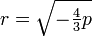$r=\sqrt{-\tfrac{4}{3} p}$ gewählt, so dass der Klammerausdruck in (2) verschwindet. Es ergibt sich

$\cos 3\alpha=-\frac{q}{2}\cdot\sqrt{-\frac{27}{p^3}}$

$\alpha=\tfrac13\arccos\left(-\frac{q}{2}\cdot\sqrt{-\frac{27}{p^3}}\right)+\frac{2}{3}k \pi$

mit ganzen Zahlen k.

Einsetzen in $z = r\cdot\cos\alpha$ liefert mit k = − 1,0,1 die folgenden drei Lösungen:

$z_2 = -\,\sqrt{-\frac{4}{3}p}\cdot \cos\left(\tfrac13\arccos\left(-\frac{q}{2}\cdot\sqrt{-\frac{27}{p^3}}\right) + \frac{\pi}{3}\right)$

$z_1 = \,\sqrt{-\frac{4}{3}p}\cdot \cos\left(\tfrac13\arccos\left(-\frac{q}{2}\cdot\sqrt{-\frac{27}{p^3}}\right)\right)$

$z_3 = -\,\sqrt{-\frac{4}{3}p}\cdot \cos\left(\tfrac13\arccos\left(-\frac{q}{2}\cdot\sqrt{-\frac{27}{p^3}}\right) - \frac{\pi}{3}\right)$

Komplexe Koeffizienten

Das Vorgehen ist für komplexe Koeffizienten weitgehend analog, es gibt aber nur zwei Fälle:

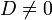• $D\ne0$: Die oben für den Fall D > 0 angegebenen Formeln gelten analog; die beiden dritten Wurzeln sind dabei so zu wählen, dass ihr Produkt 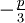$-\tfrac{p}{3}$ ergibt.
• D = 0: Die oben für den Fall D = 0 angegebenen Formeln gelten unverändert.

Weblinks

• Formeln von Cardano zur Lösung der Gleichung dritten Grades

Literatur

• Jörg Bewersdorff: Algebra für Einsteiger: Von der Gleichungsauflösung zur Galois-Theorie, Wiesbaden 2004, ISBN 3528131926, Einführung
• Heinrich Dörrie: Kubische und biquadratische Gleichungen, München 1948
• Ludwig Matthiessen: Grundzüge der antiken und modernen Algebra der litteralen Gleichungen, Leipzig 1896, Dokumenten-Server
• Peter Pesic: Abels Beweis, Springer 2005, ISBN 3-540-22285-5. Die Geschichte rund um die Lösungsformeln vom Grad 2 bis 4 und der komplette Beweis von Abel.