Heaviside-Bedingung

Die Heaviside-Bedingung, benannt nach Oliver Heaviside, ist eine Bedingung, der eine elektrische Leitung im Rahmen der Leitungstheorie genügen muss, damit keine Verzerrungen des zu übertragenden Signals auftreten. Die Erfüllung dieser Bedingung kann bei Übertragungsleitungen durch die Steigerung der Induktivität der Leitung erfolgen, wie es beispielsweise historisch durch die sogenannte bespulte Leitung erreicht wurde.

Definition

Ersatzschaltbild für ein Leitungselement einer Zweidrahtleitung der infinitesimalen Länge dx.

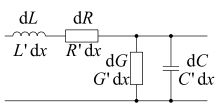
Eine Übertragungsleitung kann im Ersatzschaltbild als eine Summe von Leitungsabschnitten der infinitesimalen Länge dx, wie in nebenstehender Abbildung, dargestellt werden. Die elektrischen Eigenschaften dieses Leiters sind, bezogen auf dx: Der Induktivitätsbelag L′, der Kapazitätsbelag C′, der Widerstandsbelag R′ und der Ableitungsbelag G′. Der Widerstandsbelag und der Ableitungsbelag sorgen für Verluste in der Leitung, daher gilt für eine ideale Übertragung R' = G' = 0.

Die Heaviside-Bedingung ist erfüllt wenn gilt:

$\frac{G'}{C'} = \frac{R'}{L'}$

Bei einer üblichen Leitung mit Verzerrung gilt hingegen üblicherweise:

$\frac{G'}{C'} \ll \frac{R'}{L'}$

Hintergrund

Das Signal einer Übertragungsleitung kann auch bei einer linearen Übertragungsfunktion verzerrt werden. Die Frequenzanteile des Signals sind durch ihre Phasengeschwindigkeit frequenzabhängig. Wenn verschiedene Frequenzanteile bei verschiedenen Geschwindigkeiten übertragen werden, „verschmiert“ das Signal (Dispersion). Außerdem kann die Dämpfung der Leitung mit der Frequenz variieren (z. B. durch den Skineffekt), so dass die Signalform verändert wird.

Dies war ein großes Problem bei den ersten transatlantischen Fernmeldekabeln, das durch Untersuchungen von Lord Kelvin zu der Problematik der Dispersion führte und schließlich von Heaviside, der sich Maßnahmen dagegen überlegte, gelöst wurde. Bei zu starker Dispersion können sich nachfolgende Impulse überschneiden und zu Symbolübersprechen führen. Um dies zu verhindern musste die Schrittgeschwindigkeit auf 1/15 Baud reduziert werden. Dies ist sogar für die Morse-Übertragung sehr langsam.

Herleitung

Die Übertragungsfunktion einer Übertragungsleitung ist, unter Ausschluss von Reflexionen, definiert als:

$\frac{V_\mathrm{in}}{V_\mathrm{out}} = e^{\gamma x}$

mit der Fortpflanzungskonstante

$\gamma = \alpha +j \beta \,$

wobei α die Dämpfungskonstante und β die Phasenkonstante ist. Bei einer Verzerrung gleich 0 muss α in Abhängigkeit der Kreisfrequenz ω konstant sein, während β zu ω proportional ist. Dies ist gegeben durch die Geschwindigkeit

$v = \frac{\omega}{\beta}$

und die Tatsache das die Phasengeschwindigkeit über alle Frequenzen konstant ist.

Das Verhältnis der einzelnen Konstanten ist gegeben durch

$\gamma^2 = (\alpha +j \beta)^2 = (R+j \omega L)(G + j \omega C)\,$

die bei Verzerrungsfreiheit in der Form $\scriptstyle (A+j\omega B)^2$ gegeben sein muss. Dies gilt nur wenn sich $\scriptstyle (R+j \omega L)$ und $\scriptstyle (G + j \omega C)$ nicht um mehr als einen konstanten Faktor unterscheiden. Da beide einen Real- und Imaginärteil besitzen, müssen sich diese durch den gleichen Faktor unterscheiden, so dass gilt:

$\frac {R}{G} = \frac {j \omega L}{j \omega C}$

und damit die Heaviside-Bedingung erfüllt ist.

Eigenschaften der Leitung

Die charakteristischen Merkmale einer Leitung, die die Heaviside-Bedingung erfüllt, sind:

die Dämpfung,

$\alpha = \sqrt {RG}$

die Phasenkonstante,

$\beta = \omega \sqrt {LC}$

und die Phasengeschwindigkeit,

$v = \frac {1}{\sqrt {LC}}$

Leitungswellenwiderstand

Die Leitungswellenwiderstand einer verlustbehafteten Übertragung ist gegeben durch

$Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}}$

Es ist allgemein nicht möglich die Übertragungsleitung über alle Frequenzen genau anzupassen, da durch die Wurzel die Funktion irrational ist, so dass sie nicht als Netzwerk aus diskreten Bauelementen dargestellt werden kann. Wenn sie aber die Heaviside-Bedingung erfüllt, kann durch den Faktor

$Z_0=\sqrt{\frac{L}{C}},$

der frequenzunabhängig und rein reell ist, der Leiter nur mit Widerständen an den Enden dargestellt werden.

Dieser Faktor ist derselbe wie bei der verlustlosen Leitung ($\scriptstyle R = 0,\ G = 0$).

Literatur

• K. Küpfmüller und G. Kohn: Theoretische Elektrotechnik und Elektronik, Eine Einführung. 16. Auflage. Springer, 2005, ISBN 3-540-20792-9.

Siehe auch

• Telegraphengleichung
• Maxwell-Gleichungen