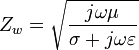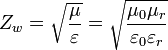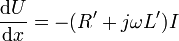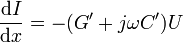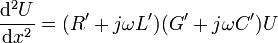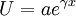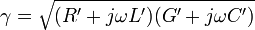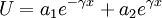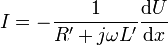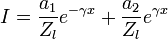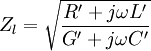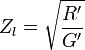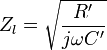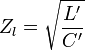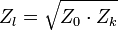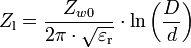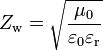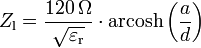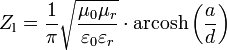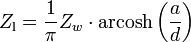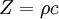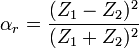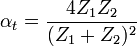Leitungswellenwiderstand

Als Wellenimpedanz – und, deutlich häufiger, Wellenwiderstand – wird eine Eigenschaft eines Mediums bezeichnet, in dem sich eine physikalische Welle ausbreitet.
Man kann ihn sich anschaulich etwa als die Härte oder Weichheit vorstellen, die das Medium der sich ausbreitenden Welle entgegensetzt. Dadurch stehen z. B. Kraft und Bewegung (bei akustischen Wellen), Strom und Spannung (bei Wellen auf elektrischen Leitungen) oder elektrischer und magnetischer Feldanteil (bei elektromagnetischen Feldwellen) in einem bestimmten Verhältnis zueinander, das Wellenwiderstand genannt wird.

Elektromagnetische Wellen

Feldwellenwiderstand

In der Elektrodynamik unterscheidet man den Leitungswellenwiderstand und den Feldwellenwiderstand. Der Feldwellenwiderstand – engl. wave impedance – kennzeichnet das Verhältnis zwischen elektrischem und magnetischem Feldanteil einer sich transversal ausbreitenden elektromagnetischen Welle. Der Feldwellenwiderstand wird aus der Quadratwurzel des Quotienten gebildet, der sich aus der im allgemeinen komplexen Permeabilität μ, der im allgemeinen komplexen Permittivität ε und der elektrischen Leitfähigkeit σ zusammensetzt. Für das Material, durch das sich die Welle bewegt, erhält man den Feldwellenwiderstand aus:

$Z_w = \sqrt {j \omega \mu \over \sigma + j \omega \varepsilon}$

Darin bezeichnet ω die Kreisfrequenz. Sofern die Welle sich nicht in elektrisch leitendem Material ausbreitet gilt:

$Z_w=\sqrt{\frac{\mu}{\varepsilon}}=\sqrt{\frac{\mu_0 \mu_r}{\varepsilon_0 \varepsilon_r}}$

Für eine elektromagnetische Welle in einem Vakuum heißt der Feldwellenwiderstand auch Freiraumwellenwiderstand. Er beträgt mit ε_r=1 und μ_r=1 im Vakuum und näherungsweise in Luft:

$Z_{w0} = \sqrt \frac{\mu_0}{\varepsilon_0} \approx 120 \pi~\Omega \approx 376{,}73~\Omega$.

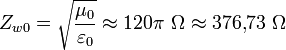Der Feldwellenwiderstand ist nicht gleich dem aus der Leitungstheorie bekannten Leitungswellenwiderstand, mit dem er häufig verwechselt wird.

Strom- und Spannungswellen auf Leitungen

Leitungswellenwiderstand

Der Leitungswellenwiderstand - engl. characteristic impedance - ist eine Kenngröße längshomogener Leitungen; dazu gehören z. B. Kabel oder Einzeldrahtanordnungen, die aus wenigstens zwei elektrischen Leitern bestehen. Die Wellenimpedanz eines Hohlleiters wird hier nicht betrachtet. Der Leitungswellenwiderstand beschreibt das Verhältnis sich in eine gemeinsame Richtung ausbreitender Strom- und Spannungswellen zueinander. In einer elektrischen Leitung sind der Leitungswellenwiderstand Z_l und der Feldwellenwiderstand Z_w über die Geometrie der Leitungsberandung miteinander verknüpft. Oft wird der Leitungswellenwiderstand auch Kabelimpedanz oder Nennimpedanz einer Leitung genannt. Hier wird der in der Lehre gängige Begriff Leitungswellenwiderstand verwendet.

Darstellung einer am Ende leerlaufenden Koaxialleitung. Ankommende Spannungspulse werden gleichphasig reflektiert, Strompulse in Gegenphase. Am Leitungsende stellt sich der Gesamtstrom aus hin- und rücklaufender Welle I=0 ein.

Darstellung einer am Ende kurzgeschlossenen Koaxialleitung. Ankommende Spannungspulse werden gegenphasig reflektiert, Strompulse mit gleicher Phase. Am Leitungsende stellt sich der Gesamtstrom aus hin- und rücklaufender Stromwelle I=2·I(hinlaufende Welle) ein.

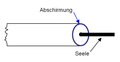
Darstellung einer mit einer Impedanz oder einer reflexionsfrei mit ihrem Leitungswellenwiderstand abgeschlossenen Koaxialleitung. Ankommende Strom- oder Spannungspulse werden nicht reflektiert, wenn der Abschlusswiderstand den Wert des Leitungswellenwiderstands besitzt. Bei anderen Werten entspricht das Verhältnis zwischen hin- und rücklaufender Welle dem Reflexionsfaktor

Der Leitungswellenwiderstand und seine Änderung entlang einer Leitung beeinflusst das Signalausbreitungsverhalten besonders, wenn die übertragenen Signale hochfrequent sind im Vergleich zur Signallaufzeit auf der Leitung oder hochfrequente Anteile enthalten.

Das ist z. B. der Fall für

• hohe Frequenzen (z. B. HF-Signale oder steilflankige Signale auf beliebigen Leitungen)
• lange Leitungen (z. B. 50-Hz-Hochspannungsleitungen über Kontinente hinweg)
• Schaltvorgänge auf Leitungen

Der Leitungswellenwiderstand homogener Hochfrequenzleitungen ist oft eine reelle Größe (z. B. 50 Ω bei gängigen Koaxialkabeln). Der Wellenwiderstand ist unabhängig von der Leitungslänge, jedoch ist er in der Regel leicht frequenzabhängig (Dispersion). Die Frequenzabhängigkeit wird durch das Dielektrikum des Kabels hervorgerufen und muss bei Breitband-Signalübertragungen berücksichtigt werden. Der Leitungswellenwiderstand ist nicht zu verwechseln mit dem ohmschen Leitungswiderstand, der die (Wärme-)Verluste beschreibt, wenn die Leitung von einem Strom durchflossen wird. Den Leitungswellenwiderstand kann man sich als Eingangswiderstand einer endlos langen, homogenen Leitung vorstellen, an der keine Reflexion entstehen kann.

Leitungsabschluss und Eingangsimpedanz einer Leitung

Den Leitungswellenwiderstand gibt es nicht im Sinne eines Bauteils. Der Sprachgebrauch „mit dem Wellenwiderstand abgeschlossen“ bedeutet, dass am Ende der Leitung ein Abschlusswiderstand mit dem Widerstandswert des Leitungswellenwiderstandes angeschlossen ist. Das kann bei hohen Frequenzen ein ohmscher Widerstand sein, da dann der Wellenwiderstand der Leitung reell ist.
Ist die Leitung nicht mit ihrem Wellenwiderstand abgeschlossen, variiert die Eingangsimpedanz der Leitung allgemein in Abhängigkeit von Leitungslänge, Betriebsfrequenz, Abschlussimpedanz und Leitungswellenwiderstand. Bei einer sogenannten RC-Leitung, die bei Niederfrequenz betrieben wird, wird der Leitungswellenwiderstand komplexwertig. In diesem Fall ist auch der Eingangswiderstand einer Leitung bei Anpassung, d. h. Leitungsabschluss mit einer Schaltung aus Widerstand (R) und Kapazität (C) komplexwertig. Die Übereinstimmung der Impedanzen von Quelle, Last und Leitungswellenwiderstand ist fast immer erwünscht. Störende Reflexionen oder Echos entstehen dann nicht und die Signalübertragung erfolgt unter geringstmöglichen Verlusten. Die Eingangsimpedanz einer mit ihrem Wellenwiderstand abgeschlossenen Leitung nimmt den Wert des Leitungswellenwiderstands an.

Der Leitungsabschluss bei Spannungspulsen

Beaufschlagt man eine homogene Leitung, die am Ausgang nicht mit dem Wellenwiderstand abgeschlossen ist, mit einem Spannungsimpuls, entsteht am Ort der Abschlussimpedanz eine Reflexion – vergleichbar einem akustischen Echo. Durch die Fehlanpassung wird ein vom Leitungswellenwiderstand abweichendes Spannungs-Stromverhältnis erzwungen, das die anteilige Reflexion der ankommenden Welle bewirkt. Der reflektierte Pulsanteil hängt vom Grad der Fehlanpassung ab. Er läuft dem ankommenden Spannungspuls entgegen. Entspricht die Quellimpedanz der Signalquelle nicht dem Wellenwiderstand der Leitung, wird das Signal an der Quellimpedanz ebenfalls als Echo reflektiert. Der Impuls läuft dann mehrmals hin- und zurück, bis seine Energie in Wärme umgewandelt ist (siehe auch Zeitbereichsreflektometrie).

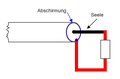
Eine mit ihrem Wellenwiderstand abgeschlossene Leitung (rechtes Bild) unterbindet die Reflexion von Spannungspulsen, soweit die Impedanz am Leitungsabschluss über das gesamte Frequenzspektrum des Pulses mit dem Leitungswellenwiderstand übereinstimmt.

Impulse bei offenem Kabelende

Impulse bei kurzgeschlossenem Kabel

Impulse bei richtig belastetem Kabel

Ersatzschaltbild einer elektrischen Leitung

Die folgende Abbildung zeigt das Ersatzschaltbild eines Leitungsabschnitts der infinitesimalen Länge dx:

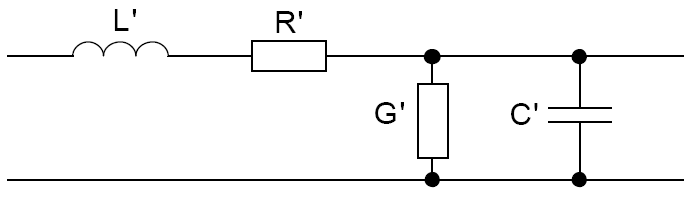
Die darin enthaltenen Größen sind auf die Länge dx bezogene Beläge: Der Induktivitätsbelag L′, der Kapazitätsbelag C′, der Widerstandsbelag R′ und der Ableitungsbelag G′. Mit der Spannung U und dem Strom I an der Leitung lassen sich mit dieser Ersatzschaltung die beiden Differentialgleichungen der homogenen Leitung bestimmen:

$\frac{\mathrm{d}U}{\mathrm{d}x} = -(R' + j\omega L') I$

$\frac{\mathrm{d}I}{\mathrm{d}x} = -(G' + j\omega C') U$

Im folgenden wird aus der Lösung des Differentialgleichungssystems der Leitungswellenwiderstand mit der Abkürzung Z_l definiert.

Herleitung des Leitungswellenwiderstandes aus der Leitungsgleichung

Differenziert man obige erste Leitungsgleichung nach x und setzt dann den Ausdruck für dI /dx aus der zweiten Gleichung ein, erhält man folgende lineare Differentialgleichung zweiter Ordnung

$\frac{\mathrm{d}^2U}{\mathrm{d}x^2} = (R' + j\omega L')(G' + j\omega C') U$

die durch einen Lösungsansatz der Form

$U = a e^{\gamma x} \,$

gelöst werden kann. Durch Koeffizientenvergleich lässt sich γ bestimmen:

$\gamma = \sqrt{(R' + j\omega L')(G' + j\omega C')}$

Damit ergeben sich zwei Lösungen für die Spannung U im Abstand x vom Leitungsanfang

$U = a_1 e^{-\gamma x} + a_2 e^{\gamma x} \,$

mit den von den Randbedingungen abhängigen Koeffizienten a₁ und a₂. Der komplexe Parameter γ wird Fortpflanzungskonstante oder auch Ausbreitungskonstante genannt. Sie ist im Allgemeinen von der Frequenz abhängig und nur bei bestimmten Leitungstypen in ihrem komplexen Wert konstant.

Die Stromstärke an der Stelle x der Leitung lässt sich aus den Leitungsgleichungen bestimmen:

$I = - \frac{1}{R' + j \omega L'} \frac{\mathrm{d}U}{\mathrm{d}x}$

Durch Einsetzen in die Lösung für die Spannung ergibt sich für den Strom I :

$I = \frac{a_1}{Z_l} e^{-\gamma x} + \frac{a_2}{Z_l} e^{\gamma x}$

Der darin auftretende Parameter Z_l definiert den Leitungswellenwiderstand in der allgemeinen Form:

$Z_l = \sqrt{\frac{R' + j\omega L'}{G' + j\omega C'}}$

Eine Berechnung der Leitungsbeläge entsprechend der Leitergeometrie und Einsetzen in die allgemeine Form des Leitungswellenwiderstands zeigt: Je enger die Leiter beieinander liegen, und je größer der Leiterquerschnitt ist, desto geringer ist der Leitungswellenwiderstand.

Frequenzabhängigkeit des Leitungswellenwiderstandes

Der Wellenwiderstand einer homogenen elektrischen Leitung ist nach obiger Gleichung im allgemeinen komplex und frequenzabhängig. Im folgenden werden gängige, technisch zulässige Vereinfachungen für Gleichstrom, niedrige und hohe Signalfrequenzen erläutert. Die Vereinfachungen können an sich frequenzunabhängig sein. Der Leitungswellenwiderstand ist es nicht. Das Diagramm in diesem Abschnitt dient der Illustration dieser Frequenzabghängigkeit. ^[1] Es zeigt die in den folgenden Unterkapiteln beschriebenen Frequenzabhängigkeiten am Beispiel des Leitungswellenwiderstands einer Drehstrom-Freileitung für 110 kV.

Der Leitungswellenwiderstand bei Gleichstrom

Bei Gleichstrom (0 Hz) verschwinden die beiden frequenzabhängigen Terme, der Imaginärteil des Leitungswellenwiderstandes wird 0, und der relativ kleine Ableitungsbelag G′ dominiert den Bruch unter der Wurzel der allgemeinen Form des Leitungswellenwiderstandes. Daher wird der Leitungswellenwiderstand bei der Frequenz 0 Hz sehr groß und reell. Typische Werte des Leitungswellenwiderstandes für Gleichstrom liegen zwischen ungefähr 100 kOhm und einigen 10 MOhm. Er wird durch folgende Gleichung beschrieben:

$Z_l = \sqrt{\frac{R'}{G'}}$

Eine mögliche Anwendung dieser Form des Leitungswellenwiderstands ist die Bestimmung des Eingangswiderstands einer Leitung im Gleichstrombetrieb nach den Gleichungen der Leitungstheorie.

Der Leitungswellenwiderstand bei niedrigen Frequenzen

Bei niedrigen Frequenzen können L′ und G′ in erster Näherung vernachlässigt werden, sodass der Leitungswellenwiderstand

$Z_l = \sqrt{\frac{R'}{j\omega C'}}$

beträgt. Die Gleichung wird z. B. angewendet, um die Werte von Widerstand und Kondensator des Leitungsabschlusses (der Gabelschaltung) in analogen Telefonen zu bestimmen. Bei richtiger Wahl der Werte werden Reflexionen verhindert, die sich als störende Echos äußern würden. In dem Beispiel ist die Telefonleitung reflexionsfrei mit ihrem Leitungswellenwiderstand abgeschlossen. Reflexionen am Leitungsende entstehen nicht. Dispersion entsteht aufgrund der Frequenzabhängigkeit des Leitungswellenwiderstands gerade im niedrigen Frequenzspektrum, auch wenn Wellenwiderstand und Abschlussimpedanz übereinstimmen und folglich die Eingangsimpedanz den Wert des Leitungswellenwiderstands annimmt.

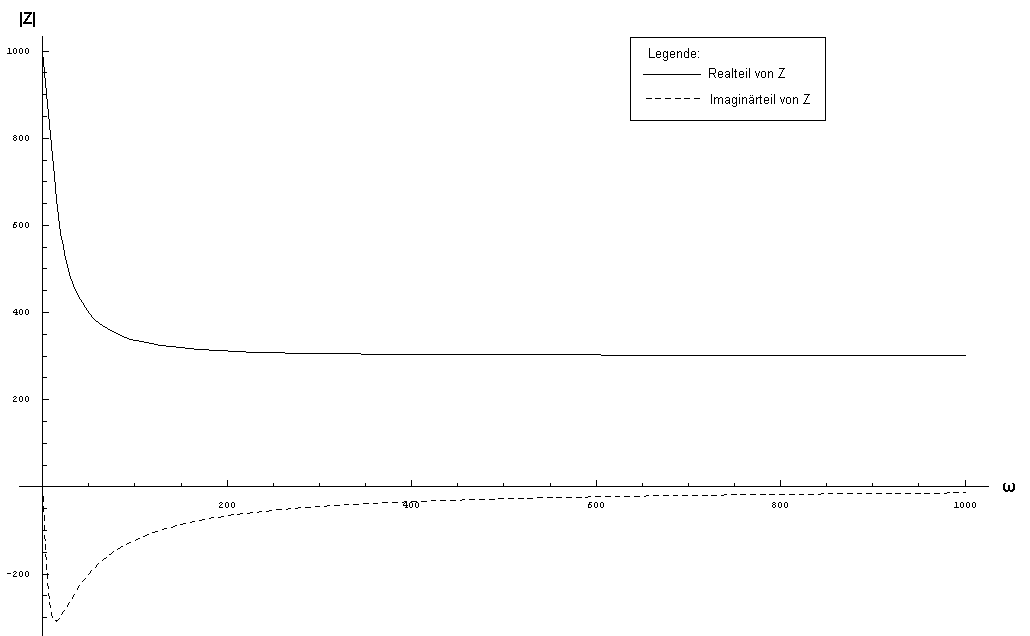Verlauf des Leitungswellenwiderstandes über der Kreisfrequenz ω. Dargestellt ist, getrennt nach Real- und Imaginärteil, der Leitungswellenwiderstand einer Freileitung mit den Parametern: R' = 0,1 Ω/km, L' = 1 mH/km, C' = 11 nF/km, G'=0,1 µS/km. Für hohe Frequenzen wird der Leitungswellenwiderstand näherungsweise reell und nähert sich in diesem Fall einem Wert von 301 Ω. Der Leitungswellenwiderstand bestimmt u. a. die natürliche Leistung einer Freileitung.

Der Leitungswellenwiderstand bei hohen und sehr hohen Frequenzen

Der Leitungswellenwiderstand nähert sich für hohe und sehr hohe Frequenzen einem frequenzunabhängigen, reellen Wert, d. h. der imaginäre Anteil wird 0. Als hohe Frequenzen gelten diejenigen, ab denen der ohmsche Widerstandsbelag R′ und der Ableitungsbelag G′ gegenüber den frequenzabhängigen Termen des kapazitiven und induktiven Belags jωC′ bzw. jωL′ der Leitung vernachlässigt werden können. Dann gleichen R′ und G′ in der Näherung Null, und der Bruch innerhalb der Wurzel der allgemeinen Form des Leitungswellenwiderstands lässt sich um jω kürzen. Bei sehr hohen Frequenzen in der Größenordnung von GHz steigen zwar R′ aufgrund des Skineffektes und G′ aufgrund des dielektrischen Verlustfaktors an, aber auch dann haben Widerstandsbelag R′ und Ableitungsbelag G′ eine immer noch untergeordnete Auswirkung auf den Leitungswellenwiderstand. Der Leitungswellenwiderstand ergibt sich für hohe und sehr hohe Frequenzen angenähert aus kapazitivem und induktivem Leitungsbelag:

$Z_l = \sqrt{\frac{L'}{C'}}$

Oft kann ab Frequenzen größer 20 kHz mit einem konstanten, reellen Leitungswellenwiderstand gerechnet werden.
Der Leitungswellenwiderstandswert beträgt dann, abhängig von der Leitungsanordnung, üblicherweise einige 10 Ohm bis einige 100 Ohm.

Messen des Leitungswellenwiderstandes

Man kann den Leitungswellenwiderstand ermitteln, indem man den Wechselstromwiderstand der offenen Leitung Z₀ und den Wechselstromwiderstand der kurzgeschlossenen Leitung Z_k misst und das geometrische Mittel beider Messwerte bildet. Der Leitungswellenwiderstand Z_l beträgt dann:

$Z_{l} = \sqrt{Z_0 \cdot Z_{k}}$

Anstelle der Bezeichnung Z_l wird oft auch die Bezeichnung Z_w (w für Welle) verwendet. Es sei nochmal darauf hingewiesen, dass dieses häufig zu Verwechslungen oder zum irrtümlichen Gleichsetzen der beiden verwandten, aber ungleichen Größen Leitungswellenwiderstand und Feldwellenwiderstand führt.

Alternativ bieten sich Zeitbereichsmessverfahren an. Hilfsmittel für die experimentelle Überprüfung sind Impulsgenerator und Oszilloskop oder ein professionelles Zeitbereichsreflektometer (TDR).

Leitungs- und Feldwellenwiderstände ausgewählter Leitungsformen

In einer Leitung bestehen am gleichen Ort ein Leitungswellenwiderstand und auch ein Feldwellenwiderstand. Der eine kennzeichnet ein natürliches Strom-Spannungsverhältnis einer Welle, der andere kennzeichnet das natürliche Verhältnis zwischen elektrischem und magnetischem Feldanteil einer elektromagnetischen Welle. Der Feldwellenwiderstand in einer Leitung hängt nur vom Material ab, der Leitungswellenwiderstand von Material und Leitungsgeometrie. Beide Werte existieren am gleichen Ort in einer Leitung nebeneinander und nehmen im Allgemeinen völlig unterschiedliche Werte an, die allerdings über die Geometrie der Leitungsberandung zueinander in Beziehung stehen.

Der Leitungswellenwiderstand lässt sich aus der Geometrie des Leiters und der Permittivität seiner Isolierung berechnen.
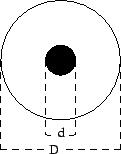
Der Leitungswellenwiderstand eines koaxialen Leiters (Koaxialkabel) beträgt bei hohen Frequenzen unter der Annahme μ_r = 1:

$Z_{\rm l} = \frac{Z_{w0}}{2 \pi \cdot \sqrt{\varepsilon_{\rm r}}}\cdot \ln \left(\frac{D}{d}\right)$

mit der relativen Dielektrizitätskonstanten ε_r des Isolationsmaterials und dem Freiraumwellenwiderstand Z_w0 (vgl. oben). Zwischen Innenleiter und Außenleiter derselben Koaxialleitung beträgt der Feldwellenwiderstand:

$Z_{\rm w} = \sqrt \frac{\mu_0}{\varepsilon_0 \varepsilon_{\rm r}}$

Dieser Feldwellenwiderstand gilt für das transversal-elektromagnetische Feld innerhalb der Isolation der Koaxialleitung. Er ist nur materialabhängig und geometrieunabhängig. Der Leitungswellenwiderstand ist materialabhängig und hängt von der Geometrie der Leiterberandung ab. Über die Geometrie von Innen- und Außenleiter ist er mit dem Feldwellenwiderstand verknüpft.

Für die Zweidrahtleitung oder Lecherleitung gilt:

$Z_{\rm l}=\frac{120\,\Omega}{\sqrt{\varepsilon_{\rm r}}}\cdot{\rm arcosh}\left(\frac{a}{d}\right)$

oder gleichwertig, aber unter Einbeziehung von μ_r:

$Z_{\rm l} = \frac{1}{\pi} \sqrt{\frac{\mu_0 \mu_r}{\varepsilon_0 \varepsilon_r}} \cdot {\rm arcosh} \left(\frac{a} {d} \right)$

Der Feldwellenwiderstand nimmt die gleiche Form an, wie bei der koaxialen Leitung, weil er nicht von der Leitungsgeometrie, sondern auch hier nur vom Isolationsmaterial abhängt. Den Zusammenhang zwischen Z_w und Z_l zeigt folgende Form obiger Gleichung für die Zweidrahtleitung:

$Z_{\rm l} = \frac{1}{\pi} Z_w \cdot {\rm arcosh} \left(\frac{a} {d} \right)$

Standardwerte

Übliche Koaxialkabel besitzen einen Leitungswellenwiderstand zwischen 50 und 75 Ω. Koaxiale Labormessleitungen besitzen üblicherweise einen Leitungswellenwiderstand von 50 Ω. Koaxiale Fernsehantennen- oder Kabelfernsehleitungen haben einen Leitungswellenwiderstand von 75 Ω. Ebenfalls üblich sind bei älteren Rundfunkempfangssystemen Zweidrahtleitungen als Antennenleitungen mit einem Wert von 240 Ω. Zweidrahtleitungen, geschirmt oder ungeschirmt, verdrillt oder parallel geführt, haben üblicherweise Leitungswellenwiderstände in der Größenordnung von 100 bis 200 Ω. Die Signaldämpfung einer Leitung hängt vom Dielektrikum zwischen den Leitern und dem Metallquerschnitt sowie dem gewählten Leitermaterial einer Leitung, aber auch vom Außendurchmesser einer koaxialen Leitung ab. Bei gegebener Frequenz erfolgt die Anpassung an andere Eingangsimpedanzwerte zum Beispiel mit Hilfe von Resonanztransformatoren.

Akustische Wellen

Für Schallwellen ergibt sich der Wellenwiderstand (s. a. Schallimpedanz) des übertragenden Mediums aus seiner Dichte ρ und der Schallgeschwindigkeit c (Ausbreitungsgeschwindigkeit) zu

$Z = \rho c \,$

Akustische Wellen erfahren in verschiedenen Medien unterschiedliche „Widerstände“; das ist die „Kennimpedanz“ dieser Werkstoffe.

Medium	Wellenwiderstand in 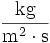$\frac{\rm kg}{\rm m^2 \cdot s}$
Wasserstoff	110
Luft	413,5 bei 20 °C (Schallkennimpedanz)
Wasser	1,48 · 106 bei 0 °C
Quecksilber	19,7 · 106

An der Grenze zweier Medien mit den Wellenwiderständen Z₁ und Z₂ wird die Schallwelle teils reflektiert, teils durchgelassen (transmittiert). Der Reflexionsgrad lautet:

$\alpha_r = \frac{(Z_1-Z_2)^2}{(Z_1+Z_2)^2}$

der Transmissionsgrad gleicht:

$\alpha_t = \frac{4 Z_1 Z_2}{(Z_1+Z_2)^2}$

Reflexionen durch Änderungen der Wellenimpedanz

An den Stellen, an denen sich der Wellenwiderstand ändert, kommt es zu Reflexionen. Die Extremfälle solcher Änderungen des Wellenwiderstandes sind offene und geschlossene Enden. Hierzu lassen sich folgende Analogien finden:

Art der Welle	Offenes Ende	Geschlossenes Ende
Elektromagn. Welle im Kabel	nicht verbunden	kurzgeschlossen
Hohlleiter	endet offen	leitfähig verschlossen
Schwingendes Seil/Saite	Ende hängt frei	Ende ist befestigt
Schall im Rohr	Ende offen	Deckel/Stopfen

In den genannten Fällen findet eine nahezu vollständige Reflexion statt (Totalreflexion). Der offene Hohlleiter strahlt allerdings einen Teil der elektromagnetischen Welle ab. Beim Kurzschluss einer Leitung wechselt der Spannungsanteil der reflektierte Welle auf einer Leitung das Vorzeichen (auch Phasensprung oder 180° Phasendrehung genannt). Bei einer elektromagnetischen Welle, die senkrecht auf eine leitfähige Schicht trifft, ist dieses für den elektrischen Feldanteil der Fall. Die reflektierte Welle läuft dann der jeweils einfallenden Welle entgegen. Reflexionen (z. B. an den Enden einer Leitung) sind Ursache stehender Wellen.

Beispiele für abgeschwächte Reflexion

Akustische Welle

• Eine Schallwelle trifft aus der Luft auf dem Wasser auf.

Elektromagnetische Welle

• Inhomogenitäten in Koaxialleitungen, v. a. übergangslose Änderung des Wellenwiderstandes an Verbindungsstellen.

Mechanische Welle

Das Ende eines zum Schwingen angeregten Seiles ist mit Gewichten beschwert oder mit einer Feder an einem festen Punkt befestigt.

Beispiele für totale Reflexion

Akustische Welle

• Eine Schallwelle trifft aus der Luft auf eine Wand (Echo).

Elektromagnetische Welle

• Eine elektrische Leitung, z. B. ein Koaxialkabel, wird am Ende kurzgeschlossen.
• Eine elektrische Leitung wird am Ende offen gelassen. Bei einem Koaxialkabel würde ein sehr kleiner Anteil der Welle nicht reflektiert, sondern über das offene Kabelende abgestrahlt.
• Eine elektromagnetische Welle trifft auf eine ausgedehnte elektrisch ideal leitende Fläche (vgl. Radarquerschnitt).

(siehe auch experimentelle Überprüfung)

Mechanische Welle

• Ein einseitig befestigtes Seil wird zu Schwingungen angeregt.

Beispiele reflexionsfreier Abschlüsse

Akustische Welle

• Schalltrichter eines Grammofons
• Exponentialtrichter bzw. -Horn und Kugelwellenhorn beim Horn (Lautsprecher).

Elektromagnetische Welle

• Der Quellwiderstand eines Senders stimmt mit dem Leitungswellenwiderstand des Kabels (z. B. 50 Ohm) und der Eingangsimpedanz des Abschlusses, z. B. der Eingangsimpedanz einer Antenne, (ebenfalls 50 Ohm) überein (siehe Impedanzanpassung).

Mechanische Welle

• Ein Seil wird über eine Feder an der Wand befestigt. Die Feder absorbiert die Wellenenergie.

Einzelnachweise

1. ↑ Karl Küpfmüller: Theoretische Elektrotechnik und Elektronik, Springer-Verlag, 14. Auflage, ISBN 3-540-56500-0, Fünftes Kapitel: Leitungen und Kettenleiter, Seite 453 bis 496

Literatur

• K. Küpfmüller und G. Kohn: Theoretische Elektrotechnik und Elektronik, Eine Einführung. 16. Auflage. Springer, 2005, ISBN 3-540-20792-9. 
• Martin Gerhard Wegener: Moderne Rundfunk-Empfangstechnik. Franzis, 1985, ISBN 3-7723-7911-7. 
• Károly Simonyi: Theoretische Elektrotechnik. 10. Auflage. Barth Verlagsgesellschaft, 1993, ISBN 3-335-00375-6, S. 545–671. 
• H.-G. Unger: Kleines Lehrbuch der Elektrotechnik, Band IX: Theorie der Leitungen. Friedr. Vieweg & Sohn GmbH, 1967, Best. Nr. 4819. 

Weblinks

• Elektronik-Kompendium – Beschreibung des Wellenwiderstandes
• Wellenausbreitung auf Leitungen der Informationstechnik
• Spannungswellen auf einer Leitung – Applet