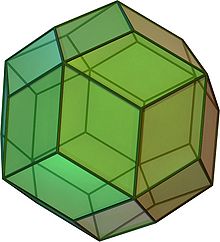
Rhombentriakontaeder

3D-Ansicht eines Rhombentriakontaeders (Animation)

Netz eines Rhombentriakontaeders

Ein Rhombentriakontaeder ist ein catalanischer Körper und dual zum Ikosidodekaeder. Es ist auch der Hüllkörper, der durch die Vereinigungsmenge der Durchdringung eines Dodekaeders und Ikosaeders beschrieben wird. Man erhält auch ein Rhombentriakontaeder, indem man gerade Pyramiden auf ein Ikosaeder oder Dodekaeder aufsetzt, von denen je zwei Seitenflächen einander zu einer ergänzen.

Das Rhombentriakontaeder besitzt 30 rhombenförmige Flächen, 32 Ecken und 60 Kanten. An 12 der Ecken grenzen 5 Kanten und an die übrigen 20 Ecken grenzen 3 Kanten an. Das Längenverhältnis der Diagonalen der Rhombenflächen entspricht exakt dem Goldenen Schnitt.

Formeln

Größen eines Rhombentriakontaeders mit Kantenlänge a
Volumen	$V = 4a^3 \sqrt{5 + 2\sqrt{5}}$
Oberflächeninhalt	$O = 12a^2 \sqrt{5}$
Inkugelradius	$\rho = a \, \sqrt{\frac{5 + 2\sqrt{5}}{5}}$
Kantenkugelradius	$r \, = \, \frac{a}{5}\left(5+\sqrt{5}\right)$
Flächenwinkel  = 144°	$cos \, \alpha = -\frac{1}{4}\left(1+\sqrt{5}\right)$

Anwendung

In Rollenspielen wird das Rhombentriakontaeder als Würfel (W30) verwendet.

Weblinks

• Eric W. Weisstein: Rhombentriakontaeder. In: MathWorld. (englisch)
• Facharbeit über das Dodekaeder und das Rhombentriakontaeder (PDF-Datei; 183 kB)

Platonische Körper

Tetraeder · Würfel · Oktaeder · Dodekaeder · Ikosaeder