- Kuboktaeder
-
 Kuboktaeder
Kuboktaeder
Ein Kuboktaeder (auch Kubooktaeder, Kubo-Oktaeder) ist ein archimedischer Körper, der durch die Schnittmenge der Durchdringung eines Hexaeders (Kubus) und eines Oktaeders beschrieben wird. In dem Namen stecken die Wörter Kubus und Oktaeder. Der zum Kuboktaeder duale Körper ist das Rhombendodekaeder.
Inhaltsverzeichnis
Beschreibung
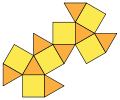
Man kann sich das Kuboktaeder auch aus 8 Tetraedern und 6 halben Oktaedern (Johnson-Körper J1: Quadratpyramide) zusammengesetzt vorstellen (vgl. Gittermodell unten).
Mit 14 Flächen (8 gleichseitige Dreiecke und 6 Quadrate), 12 Ecken und 24 Kanten gleicher Länge wird der eulersche Polyedersatz e + f − k = 2 erfüllt.
Für das Kuboktaeder gilt die Besonderheit, dass sich von jeder der 12 Ecken zum Mittelpunkt des Kuboktaeder eine „Strebe“ – mit der Länge der Kanten – anbringen lässt, sodass die dichteste Packung und damit die größte Stabilität erreicht wird.
Jeweils sechs Kanten des Kuboktaeders bilden die Kanten eines regelmäßigen Sechsecks. Es handelt sich um die gleichen Sechsecke, die man als Schnittflächen erhalten kann, wenn man ein Hexaeder (einen Würfel) auf eine bestimmte Weise in zwei Teile zerschneidet. Insgesamt gibt es vier solcher unabhängiger, gleichseitiger Sechsecke in einem Kuboktaeder (vgl. Bild unten).
Die ideale Form synthetischer Diamanten ist das Kuboktaeder.
Formeln
Größen eines Kuboktaeders mit Kantenlänge a Volumen 
Oberflächeninhalt 
Umkugelradius 
Kantenkugelradius 
Flächenwinkel
≈ 125,26° (Quadrat–Trigon)
3D-Kantenwinkel
= 120°
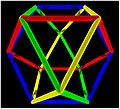
Jitterbug-Transformation
In Buckminster Fullers sogenannter „Jitterbug-Transformation“ Platonischer Körper ist das Kuboktaeder das ausgedehndeste Stadium. Aus seinen in den Ecken mit Kugelgelenken miteinander verbunden gedachten 24 Kanten entsteht durch Verdrehen ein Ikosaeder (6 seiner 30 Kanten sind virtuell, müssen gedacht werden). Nach weiterem Verdrehen stoßen die Kanten Paar-weise zusammen, wobei ein Oktaeder entsteht. Nach weiterem Verdrehen ist ein Tetraeder entstanden, wobei je 4 Kanten zusammengefallen sind. Dieser Platonische Körper mit kleinstem Volumen lässt sich schließlich in ein ebenes Dreieck zusammenklappen, bei dem je 8 Kanten zusammenfallen.[1]
Wird ein Flächen-Modell des Oktaeders der Jitterbug-Transformation unterworfen, so lässt sich dieses über das Ikosaeder zum noch größeren Kuboktaeder umwandeln.[2] Auf der Forschungsausstellung Heureka in Zürich 1991 wurde am begehbaren „Heureka-Polyeder“ diese Transformation gezeigt. Während der Veränderung wurden die Besucher im Inneren auf einer Hebebühne synchron mit auf- und abbewegt.
- Jitterbug-Transformation zwischen Oktaeder und Kuboktaeder
Einzelnachweise
- ↑ Demonstration der Jitterbug-Transformation zwischen Dreieck und Kuboktaeder [1]
- ↑ Demonstration der Jitterbug-Transformation zwischen Oktaeder und Kuboktaeder [2]
Weblinks
- Eric W. Weisstein: Kuboktaeder. In: MathWorld. (englisch)
- http://www.mathematik.uni-bielefeld.de/~ringel/puzzle/puzzle03/kubokta.htm
- Mathematische Basteleien – Kuboktaeder
Wikimedia Foundation.