- Cauchy-Hadamard
-
Der Konvergenzbereich ist in der Analysis, einem Teilgebiet der Mathematik, einer Funktionenreihe zugeordnet und bezeichnet die Menge aller derjenigen Punkte im Definitionsbereich, in dem die Funktionenreihe absolut konvergiert. Insbesondere für Potenzreihen ist der Konvergenzbereich eine Kreisscheibe um den Entwicklungspunkt, deren Radius Konvergenzradius genannt wird.
Inhaltsverzeichnis
Definition
Sei (M,d) ein metrischer Raum und (E,||.||) ein Banachraum. Es sei eine Folge von stetigen Funktionen
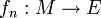 gegeben. Dann
gegeben. Dann- konvergiert die Reihe
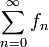 im Punkt
im Punkt 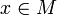 , falls die Folge der Partialsummen <Sk(x)>,
, falls die Folge der Partialsummen <Sk(x)>, 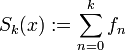 , die eine Punktfolge im Wertebereich E ist, konvergiert.
, die eine Punktfolge im Wertebereich E ist, konvergiert. - konvergiert die Reihe
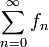 absolut im Punkt
absolut im Punkt 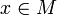 , falls die Zahlenreihe über die Normen der Summanden
, falls die Zahlenreihe über die Normen der Summanden 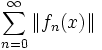 konvergiert.
konvergiert.
Die kleinste abgeschlossene Menge, die alle Punkte
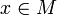 des Definitionsbereichs enthält, in denen absolute Konvergenz vorliegt, wird Konvergenzbereich genannt.
des Definitionsbereichs enthält, in denen absolute Konvergenz vorliegt, wird Konvergenzbereich genannt.Bemerkung: In Randpunkten dieser Menge muss keine absolute Konvergenz vorliegen, die entsprechende Reihe im Wertebereich kann auch divergent sein.
Majorantenkriterium
- Gibt es eine konvergente Reihe
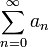 mit positiven reellen Gliedern und ein Gebiet
mit positiven reellen Gliedern und ein Gebiet 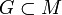 mit
mit 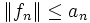 für alle
für alle 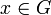 und alle
und alle 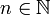 , so ist G eine Teilmenge des Konvergenzbereichs. Die Konvergenz ist auf G gleichmäßig, damit ist die durch die Reihe auf G definierte Funktion F auf G stetig.
, so ist G eine Teilmenge des Konvergenzbereichs. Die Konvergenz ist auf G gleichmäßig, damit ist die durch die Reihe auf G definierte Funktion F auf G stetig. - Ist
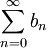 eine divergente Reihe mit positiven reellen Gliedern und gilt auf einem Gebiet D⊆M ||fn(x)||>bn für alle x∈D und alle n∈ℕ, so ist G eine Teilmenge im Komplement des Konvergenzbereichs.
eine divergente Reihe mit positiven reellen Gliedern und gilt auf einem Gebiet D⊆M ||fn(x)||>bn für alle x∈D und alle n∈ℕ, so ist G eine Teilmenge im Komplement des Konvergenzbereichs.
- Siehe auch: Majorantenkriterium
Anwendung auf komplexe Potenzreihen – Satz von Cauchy-Hadamard
Sei
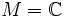 ,
, 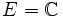 und
und 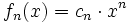 mit
mit 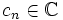 für jedes
für jedes 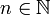 , d.h. die Funktionenreihe
, d.h. die Funktionenreihe 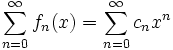 sei eine komplexe Potenzreihe. Dann gilt:
sei eine komplexe Potenzreihe. Dann gilt:- Die offene Kreisscheibe B(0,r) um den Nullpunkt mit Radius r>0 gehört zum Konvergenzbereich, falls |cn|∙rn<1 für fast alle
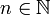 erfüllt ist.
erfüllt ist. - Das Komplement der Kreisscheibe B(0,R) liegt außerhalb des Konvergenzbereichs, wenn |cn|∙Rn>1 für unendlich viele
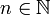 gilt.
gilt. - Der Konvergenzbereich ist eine Kreisscheibe um den Nullpunkt mit dem Konvergenzradius
![r=(\limsup_{n\to\infty}\sqrt[n]{|c_n|})^{-1}](/pictures/dewiki/98/bf01ec1637380e7cf0eb2a72c9a31599.png) , falls diese Zahl existiert. Andernfalls ist der Konvergenzbereich ganz
, falls diese Zahl existiert. Andernfalls ist der Konvergenzbereich ganz  .
.
Beispiele
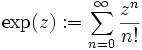 konvergiert überall absolut.
konvergiert überall absolut.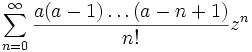 konvergiert in der Einheitskreisscheibe absolut gegen (1 + z)a
konvergiert in der Einheitskreisscheibe absolut gegen (1 + z)a
- konvergiert die Reihe
Wikimedia Foundation.
