Kreistreue

Eine geometrische oder mathematische Abbildung heißt kreistreu, wenn das Bild eines beliebigen Kreises stets wiederum ein Kreis ist. Die Eigenschaft wurde um 130 v. Chr. vom antiken Astronomen Hipparchos beim Bau eines Astrolabiums entdeckt, als er die stereografische Projektion zur Abbildung der Himmelskugel auf die Ebene verwendete.

Triviale Beispiele für kreistreue Abbildungen sind unter anderem alle Achsen- und Punktspiegelungen, allgemeiner alle Kongruenzabbildungen und alle Ähnlichkeitsabbildungen.

Kreistreue der stereografischen Projektion

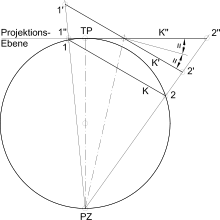Nachweis der Kreistreue (schiefachsige Projektion):
die Strahlen aus dem Projektionszentrum PZ an den Urkreis K (Durchmesserpunkte 1 und 2) bilden einen schiefen Kreiskegel, dessen zu K paralleler Schnitt K' kreisförmig ist; die Projektionsebene K‘’ schneidet die Kegelachse gleich schräg wie der Schnitt K', weshalb die in ihr liegende Schnittfigur ebenfalls ein Kreis ( Punkte 1‘’ und 2‘’) ist

Die Kreistreue dieser ebenen Abbildung einer Kugel besagt, dass Kreise auf dem Urbild (der Himmels- oder Erdkugel) in der Bildebene ebenfalls kreisförmig abgebildet werden. Die Eigenschaft (die hier zusätzlich zur Winkeltreue besteht) ermöglichte schon früh die relativ einfache Konstruktion genauer Sternkarten, Navigationskarten oder von Ziffernblättern astronomischer Uhren. Die kreisförmigen Sternbahnen am Himmel ließen sich mit Zirkeln auf ebene Scheiben gravieren, indem jeweils zwei gegenüberliegende Punkte des darzustellenden Kreises projiziert wurden.

Breitenkreise einer polaren stereografischen Projektion

Direkt einsichtig ist die Kreistreue einer polaren Projektion (siehe Abbildung, unten), bei der die Kugel vom Südpol auf eine im Nordpol tangierende Ebene abgebildet wird. Dabei werden Äquator und alle Breitenkreise zu konzentrischen Kreisen um den Nordpol über.
Allerdings wird der Bildäquator doppelt so groß wie sein Urbild, und der südliche Wendekreis (geografische Breite -23,5°) bereits über 3x größer. Die Längenkreise bilden sich zu geraden Linien durch den Nordpol ab, die alle Breitenkreise senkrecht schneiden.

Dass auch schräg zum Äquator verlaufende Groß- oder Kleinkreise kreisförmig abgebildet werden, lässt sich folgendermaßen veranschaulichen: Die Projektionsstrahlen entlang des abzubildenden Kleinkreises bilden einen elliptischen Kegel, der von der Projektionsebene im selben Winkel wie das Urbild geschnitten wird, was ebenfalls Kreisform ergibt (siehe nebenstehende Abbildung).

Schiefachsige stereografische Projektion

Bei allgemeiner Lage der Erdachse sind die Breitenkreise eine Serie zwar konzentrischer, aber schräger Kreise auf dem Urbild. Ihre Abbilder umschließen einander, sind aber nicht mehr konzentrisch - denn ihre vom Projektionszentrum entferntere Hälfte wird länger abgebildet als die nähere Hälfte. Alle Kreismittelpunkte liegen jedoch auf der Strecke zwischen dem Kartenmittelpunkt (Hauptpunkt der Projektion) und dem Bild des Nordpols.

Elementargeometrisch lässt sich zeigen, dass der Mittelpunkt des Bildkreises als Urbildpunkt die Spitze eines geraden Kreiskegels hat, dessen Grundfläche der Urbildkreis ist, und dessen Mantellinien Tangenten an die Kugel sind. Jeder Kleinkreis besitzt einen solchen Tangentenkegel. Bei einem schräg zur Erdachse liegenden Großkreis (z. B. der Ekliptik oder dem Horizontkreis) wird der Tangentenkegel zu einem Zylinder, was die geometrische Konstruktion der Abbildung wesentlich erleichtert.

Stereografische Anwendungen

Stereographische Projektion des nördlichen Sternen-Himmels auf einem Astrolabium

Polare stereographische Projektion der Erde

In der Antike wurde die stereografische Projektion vor allem zur geometrischen Konstruktion von Sternkarten, Sonnenuhren und Astrolabien verwendet. Neben der Kreis- ist hier auch die Winkeltreue von Nutzen. Weil die Abbildung aber nach außen eine deutlich wachsende Streckenverzerrung aufweist, erscheinen z.B. bei einer polaren Sternkarte die südlicheren Sternbilder größer als die nördlicheren.

Die heute am Markt angebotenen drehbaren Sternkarten sind daher nicht streng stereografisch projiziert, sondern ein aphylaktischer "Kompromiss": die horizontnahen Sternbilder erscheinen zwar vergrößert, aber nur etwa im halben Ausmaß. Als Folge ist aber der Horizont kein Kreis, sondern ein Oval.

In der Navigation benützt man die stereografische Projektion zur Darstellung der Polargebiete jenseits von etwa 75° geografische Breite. In der Kristallografie und in der Geophysik stellt man die räunliche Orientierung von Kristallflächen und von Klüften stereografisch dar.

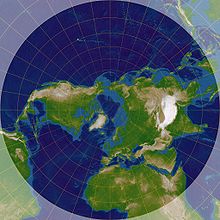
Von Geografen und Kartografen wird bisweilen die äquatoriale Projektion zur Darstellung von Planigloben verwendet. Das nebenstehende Bild zeigt das kreisförmige Kartennetz, wobei die Abstände der Breitenkreise zu den Polen hin zunehmen.