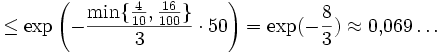- Chernoff-Schranke
-
In der Wahrscheinlichkeitstheorie beschreibt die nach Herman Chernoff benannte Chernoff-Ungleichung eine obere Schranke für die Wahrscheinlichkeit, dass eine Sequenz unabhängiger Bernoulli-Experimente von ihrer erwarteten Anzahl an Erfolgen abweicht.
Die Chernoff-Ungleichung ist ein vielseitiges und vielfach verwendetes Hilfsmittel bei der Analyse von randomisierten Algorithmen in der Informatik.
Inhaltsverzeichnis
Satz
Sei
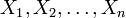 eine Sequenz von n unabhängigen Bernoulli-Experimenten mit
eine Sequenz von n unabhängigen Bernoulli-Experimenten mit ![\Pr[X_i=1] = p](/pictures/dewiki/53/5570157982223578d4b2313dc2b1d263.png) und
und ![\Pr[X_i=0] = 1-p](/pictures/dewiki/99/cf69a65912558936ced3b9f2665ed0e8.png) . Demnach beschreibt pn die erwartete Anzahl an Erfolgen (Xi = 1) des Experiments.
. Demnach beschreibt pn die erwartete Anzahl an Erfolgen (Xi = 1) des Experiments.- 1. Dann gilt für jedes δ > 0
- 2. Für jedes
![\delta \in [0,1]](/pictures/dewiki/56/8d7a7f3ee82cdf6e2936e5e1f351adef.png) gilt:
gilt:
Beweis der ersten Chernoff-Schranke
Sei t > 0 eine zunächst beliebige Konstante. Bezeichne Y im Folgenden zur Vereinfachung der Schreibweise eine neue Zufallsvariable vermöge
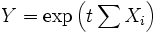 . Auf Grund der Monotonie der Abbildung
. Auf Grund der Monotonie der Abbildung 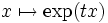 folgt dann
folgt dann![\Pr\left[ \sum X_i \geq (1+\delta)\cdot pn \right]
= \Pr\left[Y \geq \exp\left(t(1+\delta)\cdot pn\right) \right]
= \Pr\left[Y \geq k \textrm{E}\left[Y\right] \right]
\leq \frac{1}{k}](/pictures/dewiki/55/79abc53bda42b81c2d08ad3c96fce60e.png) ,
,
wobei k als
![k = \frac{\exp(t(1+\delta)pn)}{\textrm{E}[Y]}](/pictures/dewiki/54/67b0614cad8b6d5af312949a6fcc79a1.png) definiert ist und die letzte Abschätzung mittels Markow-Ungleichung folgt. Nun gilt
definiert ist und die letzte Abschätzung mittels Markow-Ungleichung folgt. Nun giltund somit
![\textrm{E}\left[ Y \right]
= \textrm{E}\left[ \exp(t\sum X_i) \right]
= \textrm{E}\left[ \prod \exp(tX_i) \right]
= \prod \textrm{E}\left[ \exp(tX_i) \right]
= \left(1 + (e^t-1)p\right)^n](/pictures/dewiki/101/e5de45c775d700070d303a56e0bb5beb.png) .
.
Damit folgt
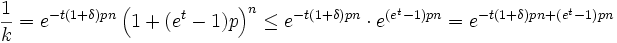 .
.
Betrachte nun t = log(1 + δ). Dann gilt
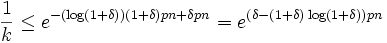 .
.
Für einen Teil des Exponenten des rechten Terms
- L(δ) = (1 + δ)log(1 + δ)
kann man mittels Kurvendiskussion und Taylor-Reihenentwicklung zeigen, dass stets
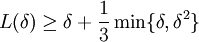 gilt. Auf Grund der Monotonie der Exponentialfunktion gilt:
gilt. Auf Grund der Monotonie der Exponentialfunktion gilt: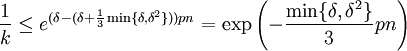 . Zusammen mit der ersten Abschätzung folgt die Behauptung.
. Zusammen mit der ersten Abschätzung folgt die Behauptung.Beweis der zweiten Chernoff-Schranke
Der Beweis der zweiten Schranke folgt technisch analog zur ersten Schranke.
Varianten
- Eine allgemeine Variante der Chernoff-Ungleichung lässt sich mittels der Standardabweichung formulieren. Seien
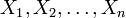 diskrete, unabhängige Zufallsvariablen mit E[Xi] = 0 und
diskrete, unabhängige Zufallsvariablen mit E[Xi] = 0 und 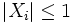 . Bezeichne σ2 die Varianz von
. Bezeichne σ2 die Varianz von 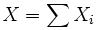 . Dann gilt für jedes
. Dann gilt für jedes 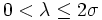 :
:
-
- Der Beweis ist technisch analog zu dem oben gezeigten.
Beispiele
- Betrachte die folgende Frage: Wie wahrscheinlich ist es, beim zehnmaligen Wurf einer fairen Münze wenigstens siebenmal das Ergebnis "Zahl" zu erhalten? Die Münzwürfe stellen Bernoulli-Experimente
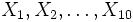 mit
mit 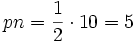 dar. Somit folgt nach der ersten Chernoff-Ungleichung:
dar. Somit folgt nach der ersten Chernoff-Ungleichung:
- Man formuliere das obige Beispiel nur leicht um und frage stattdessen: Wie wahrscheinlich ist es, bei hundertmaligem fairen Münzwurf wenigstens siebzigmal das Ergebnis "Zahl" zu erhalten? Sofort erweist sich die erste Chernoff-Schranke als deutlich stärker:
Literatur
- Christian Schindelhauer, Algorithmen für Peer-to-Peer Netzwerke (Vorlesungsmaterialien), http://wwwcs.upb.de/cs/ag-madh/WWW/Teaching/2004SS/AlgoP2P/skript.html, Universität Paderborn, 2004.
- Kirill Levchenko, Notizen, http://www.cs.ucsd.edu/~klevchen/techniques/chernoff.pdf
- 1. Dann gilt für jedes δ > 0
Wikimedia Foundation.

![\Pr\left[ \sum X_i \geq (1+\delta)\cdot pn \right]
\leq \exp\left( -\frac{\min\{\delta,\delta^2\}}{3}pn \right)](/pictures/dewiki/56/8814f7d24d9bd7688eafc81b049cc889.png)
![\Pr\left[ \sum X_i \leq (1-\delta)\cdot pn \right]
\leq \exp\left( -\frac{\delta^2}{2}pn \right)](/pictures/dewiki/48/07de6629c098b5cd97df18cd0308f121.png)
![\textrm{E}\left[ \exp(tX_i) \right]
= (1-p) e^0 + p e^t
= 1 + (e^t-1)p](/pictures/dewiki/99/cf7dd9e06545d6bbfec59e64f30f5a37.png)
![\Pr\left[\left|\sum X_i\right| \geq \lambda\sigma\right] \leq 2 \exp(-\frac{\lambda^2}{4})](/pictures/dewiki/57/95f1056c0b9fa32f4d7144d32c486d25.png)
![\Pr\left[ \sum X_i \geq 7 \right] = \Pr\left[ \sum X_i \geq (1+\frac{4}{10})\cdot 5 \right]](/pictures/dewiki/50/209d7050c4b3053af1b0ba851b926761.png)
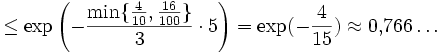
![\Pr\left[ \sum X_i \geq 70 \right] = \Pr\left[ \sum X_i \geq (1+\frac{4}{10})\cdot 50 \right]](/pictures/dewiki/100/d49bba136bfa459028b02902b2fc23ce.png)