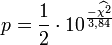Chi-Quadrat-Vierfeldertest

Die Artikel Vierfelderkorrelation und Vierfeldertest überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Pjacobi 14:22, 4. Jul. 2008 (CEST)

Der Vierfeldertest (auch χ²-Vierfeldertest bzw. Chi-Quadrat-Vierfeldertest) ist ein statistischer Test. Er dient dazu, die Häufigkeit eines Merkmals in zwei stochastisch unabhängigen Gruppen zu vergleichen und zugleich die Frage nach der Signifikanz des Testes zu beantworten.

Bei der Frage, ob eine medizinische Maßnahme wirksam ist oder nicht, ist der Vierfeldertest sehr hilfreich, da er sich auf das Hauptentscheidungskriterium konzentriert.

Eine Erweiterung des Vierfeldertests ist der Phi-Koeffizient. Zwischen 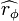$\widehat{r_\phi}$, der Anzahl der Beobachtungen n und der Prüfgröße des Chi-Quadrat-Vierfeldertests besteht der Zusammenhang $\widehat{\chi^2}=n \cdot \widehat{r_\phi}^2$.

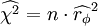Der englische Fachbegriff für den Vierfeldertest heißt Cross tab oder Fourfold Test.

Rechenvorschrift

Um den Vierfeldertest zu verstehen, stellt man sich eine Tabelle folgender Art zusammen:

	Erfolg	Misserfolg	Summe
Stichprobe 1	a	b	a+b
Stichprobe 2	c	d	c+d
Summe	a+c	b+d	n = a+b+c+d

Um festzustellen, ob die Stichproben wesentlich und wie groß die Wahrscheinlichkeit für einen Zufallsbefund ist, wird zunächst die Prüfsumme berechnet:

$\widehat{ \chi^2} = \frac{n \cdot (a\cdot d-c\cdot b)^2}{(a+c)\cdot(b+d)\cdot(a+b)\cdot(c+d)}$.

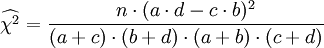Diese Formel darf allerdings nur dann verwendet werden, wenn in jeder der beiden Stichproben mindestens sechs Merkmalsträger enthalten sind.

Alternativ kann man die Vierfeldertafel auch mit dem Chi-Quadrat-Test auswerten (Anleitung siehe dort).

Entscheidungsfindung

In der Medizin wird ein Vergleich zwischen beiden Stichproben meistens dann als wesentlich anerkannt, wenn die Wahrscheinlichkeit für einen Zufallsbefund kleiner oder gleich 5 % ist (das sog. Niveau α des Tests). Errechnet sich eine Prüfsumme die kleiner als 3,841 ist, dann konnte der Test nicht nachweisen, dass ein signifikanter Unterschied besteht, errechnet sich dagegen eine Prüfsumme, die gleich oder größer 3,841 ist, so besteht zwischen den Stichproben ein signifikanter Unterschied.

Faustformel zur Anwendbarkeit

Der Erwartungswert aller vier Felder muss mindestens 5 betragen. Der Erwartungswert wird dabei berechnet aus Zeilensumme*Spaltensumme/Gesamtzahl. Bei einem Erwartungswert kleiner 5 empfehlen Statistiker den Exakten Fisher-Test.

Tabelle für Prüfsummen

Prüfsumme	Wahrscheinlichkeit für Zufall
2,71	10,0%
3,84	5,0%
6,64	1,0%
10,83	0,1%

Die Wahrscheinlichkeit für einen Zufall einer Prüfsumme lässt sich wie folgt berechnen:

$p=\frac{1}{2} \cdot 10^\frac{-\widehat{\chi^2}}{3{,}84}$

Beispiel 1

Man befragt 50 Frauen, ob sie rauchen oder nicht. Dasselbe macht man mit 50 Männern. Man erhält das Ergebnis:

• FRAUEN : 25 Raucher 25 Nichtraucher
• MÄNNER : 30 Raucher 20 Nichtraucher

Führt man mit diesem Ergebnis einen Vierfeldertest durch, dann ergibt sich anhand der oben dargestellten Formel die Prüfsumme mit ungefähr dem Wert 1. Da diese Prüfsumme kleiner ist als 3,841, besteht kein signifikanter Unterschied.

Beispiel 2

• Frauen: 250 Nichtraucher 250 Raucher
• Männer: 300 Nichtraucher 200 Raucher

Hier ergibt sich anhand des Vielfeldertestes der Prüfwert 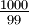$\tfrac{1000}{99}$, welcher größer als 3,841 ist. Somit besteht ein signifikanter Unterschied.

Siehe auch

• Chi-Quadrat-Test
• Confusion Matrix
• exakter Test nach Fisher

Weblinks

• Applet für den Vierfeldertest
• Delphi Programm für den Vierfeldertest
• Maple 10 Classic Worksheet mit Übungen
• Entwickler des Vierfeldertests
• Kurzüberblick über den Vierfeldertest
• Progammcode in Visual Basic
• Progammcode in Gambas