Reflektometrische Dünnschichtmessung

Die Reflektometrische Dünnschichtmessung ist ein Messverfahren, das auf den Prinzipien der Dünnschichtinterferenz beruht, und dazu dient, die Schichtdicke von dielektischen Dünnschichten zu bestimmen. Außerdem kann aus den Daten der Brechungsindex des Materials gewonnen werden. Diese Informationen sind von zunehmender Bedeutung, da Dünnschichten heutzutage vielfach eingesetzt werden, z. B. bei Antireflexionsbeschichtungen, der Beschichtung von medizinischen Implantaten oder in der Solarindustrie.

Theorie

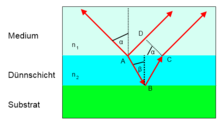
Als Dünnschicht wird eine Materialschicht mit einer Dicke im Nano- bis Mikrometerbereich bezeichnet. Einfallendes Licht wird an der Grenze Material–Umgebungsmedium (zumeist Luft) entweder reflektiert oder transmittiert; das transmittierte Licht wiederum trifft auf die Grenzfläche Dünnschicht–Substrat und wird hier wiederum reflektiert. Wie viel Licht hierbei reflektiert bzw. transmittiert wird, lässt sich mit Hilfe der Fresnel-Gleichungen bestimmen. Zwischen den an den beiden Grenzflächen reflektierten Anteilen kommt es in der Folge zu konstruktiver bzw. destruktiver Interferenz. Diese ist dabei abhängig von der Schichtdicke d, dem Brechungsindex n des Materials sowie dem Einfallswinkel α des Lichts. Außerdem kann es zu einer Phasenverschiebung um 180° bzw. π kommen.

Strahlengang bei der Dünnschichtinterferenz

Der optische Weg (OPD) des einfallenden Lichts lässt sich anhand der Abbildung folgendermaßen berechnen:

$\mathrm{OPD} = n_2 (\overline{\mathrm{AB}} + \overline{\mathrm{BC}})- n_1(\overline{\mathrm{AD}})$

sowie

$\overline{\mathrm{AB}} = \overline{\mathrm{BC}} = \frac{d}{\cos(\beta)}$

$\overline{\mathrm{AD}} = 2d\tan(\beta)\sin(\alpha)$

Nach Snellius folgt

n₁sin(α) = n₂sin(β)

und damit

$\mathrm{OPD} = n_2\left(\frac{2d}{\cos(\beta)}\right) - 2d\tan(\beta)n_2\sin(\beta)$

$\mathrm{OPD} = 2n_2d\left(\frac{1-\sin^2(\beta)}{\cos(\beta)}\right)$

$\mathrm{OPD} = 2n_2d\cos\big(\beta)$

Bei der reflektometrischen Schichtdickemessung wird das Licht einer Weißlichtquelle in einem Winkel von 90° auf die zu messende Schicht gelenkt und mit Hilfe eines Spektrometers die Reflexion in Abhängigkeit der Wellenlänge gemessen. Aus der obigen Gleichung ergibt sich mit $\cos(0^\circ) = 1$, dass nur für bestimmte Wellenlängen konstruktive Interferenz auftritt und diese Wellenlängen direkt abhängig sind von der Schichtdicke und dem Brechungsindex.

$\lambda = \frac{2n_2 d }{m}$

So ergibt sich ein charakteristisches Oszillationsmuster, dessen Frequenz direkt von der Schichtdicke abhängt: Je dicker die Schicht ist, desto höher ist auch die Frequenz. So kann bei bekanntem Brechungsindex auf die Schichtdicke geschlossen werden. Andererseits ist es möglich, bei bekannter Schichtdicke d den Brechungsindex n₂ zu bestimmen.

Literatur

• Eugene Hecht: Optics. Addison Wesley, 2002, ISBN 0321188780.