Standardisierungsproblem

Das Standardisierungsproblem gehört zum Forschungsgebiet der Wirtschaftsinformatik und behandelt die Fragestellung, ob und inwieweit Komponenten in Informationssystemen zu standardisieren sind.

Hintergründe

In vielen Unternehmen oder Unternehmensverbünden sind die Anwendungssysteme historisch und zum Teil unkoordiniert gewachsen. Dies führt zu heterogenen IT-Landschaften, die den Informationsaustausch zwischen verschiedenen Bereichen durch Inkompatibilitäten erschweren.

Der Einsatz von Standards stellt eine wesentliche Maßnahme zur Reduzierung dieser Integrationskosten dar. Standards werden entweder von anerkannten Standardisierungsorganisationen in einem geregelten Verfahren verabschiedet (in diesem Fall spricht man von Normen) oder aber sie entstehen ungeregelt durch eine hohe Verbreitung (De-facto-Standards). Beispiele sind die unternehmensübergreifende Anwendung von EDI-Standards oder eine SOA-Plattform, die idealerweise eine reibungslose Integration von Services unterschiedlicher Anbieter auf der Basis von Web-Service-Standards ermöglicht.

Modellierung des Standardisierungsproblems

Grundlage des Standardisierungsproblems ist ein Graph, der aus n Knoten besteht. Die Knoten können menschliche oder maschinelle Aufgabenträger sein, welche Informationen speichern, verarbeiten und untereinander austauschen. Für diese Aufgaben existieren Standards. Die Standardisierung eines Systemelements verursacht Standardisierungskosten (z. B für die Anschaffung von Software oder die Schulung menschlicher Aufgabenträger), vereinfacht aber die Informationsübertragung, sodass sog. Informationskosten eingespart werden können. Diese setzen sich aus Kommunikationskosten (z. B Kosten für die manuelle Bearbeitung und Übertragung von Geschäftsdokumenten) und Friktionskosten (Opportunitätskosten einer schlechten Entscheidung, die auf mangelnden Informationen wegen der nichtstandardisierten Übertragung basieren) zusammen. Vereinfachend wird angenommen, dass es eine zentrale Entscheidungsinstanz für alle betrachteten Systemelemente gibt.

Im Modell sind die Systemelemente S_i als Knoten dargestellt. Die Standardisierung eines Knotens S_i verursacht Standardisierungskosten über den gesamten Planungszeitraum in Höhe von a_i .

Die Entscheidung über die Standardisierung eines Knotens wird mit Hilfe der binären Aktionsvariablenx_i modelliert. $x_i =\begin{cases} 1, & \text{wenn der Standard auf }S_i\text{ implementiert wird,}\\ 0, & \text{ wenn der Standard auf }S_i\text{ nicht implementiert wird.} \end{cases}$

Die Kante zwischen zwei Knoten repräsentiert den Übertragungsweg für Informationen. An der Kante sind die Informationskosten e_ij dargestellt, die über den gesamten Planungszeitraum eingespart werden können, wenn beide Knoten standardisiert sind. Die Informationskosten e_ij zwischen zwei Knoten S_i und S_j werden also genau dann eingespart, wenn S_i und S_j standardisiert sind, also x_i = x_j = 1. Die Zielfunktion des Entscheidungsproblems lautet dann: $\sum_{i=1}^n a_i x_i + \sum_{i=1}^n\sum_{j=1,\atop i \neq j}^n e_{ij} (1-x_i \cdot x_j) \rightarrow \min!$

Beispiel

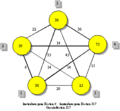
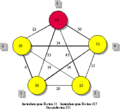
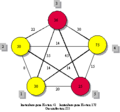
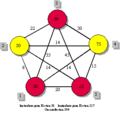
Der Trade-off zwischen knoten- und kantenbezogenen Kosten kann anhand eines sehr einfachen 5-Knoten-Problems mit einem Standard erläutert werden. Die Zahlen in den Knoten repräsentieren dabei die Kosten der Standardisierung der jeweiligen Knoten. An den Kanten zwischen jeweils zwei Knoten sind die realisierbaren kantenbezogenen Kosteneinsparungen abgetragen. Wie bereits erwähnt, lassen sich diese kantenbezogenen Kosten zwischen zwei Knoten einsparen, wenn beide standardisiert werden.

• 

  unstandardisiert

• 

  ein Knoten standardisiert

• 

  zwei Knoten standardisiert

• 

  drei Knoten standardisiert

In der Abbildung links oben sei kein Knoten standardisiert, was wir dadurch kennzeichnen, dass die Knoten gelb dargestellt sind. Bei dieser Konstellation entstehen keine Standardisierungskosten, es sind jedoch alle kantenbezogenen Kosten zu tragen. Daraus resultieren Gesamtkosten in Höhe von 217 Geldeinheiten (GE). Bei der Konstellation, wie sie in der Abbildung rechts oben eingezeichnet ist, wird lediglich der Knoten 3 standardisiert. Das bedeutet, dass Standardisierungskosten in Höhe von 36 GE zu tragen sind. Da sich jedoch mit der Nutzung eines Standards auf nur einem Knoten noch kein Informationsaustausch unterstützen lässt (was nutzt es, als einziger ein Fax-Gerät oder einen E-Mail-Account zu haben), betragen die kantenbezogenen Kosten weiterhin 217 GE, was zu Gesamtkosten in Höhe von 253 GE führt. Wird nun darüber hinaus Knoten 5 standardisiert, so betragen die Standardisierungskosten insgesamt 61 GE (Abbildung links unten). Dafür werden jedoch die kantenbezogenen Kosten zwischen diesen beiden Knoten in Höhe von 45 GE eingespart, was zu Gesamtkosten von 233 GE führt. Wird mit Knoten 1 ein weiterer Knoten standardisiert (Abbildung rechts unten), so steigen die Standardisierungskosten weiter um 30 GE; dafür werden nun die kantenbezogenen Kosten zwischen den drei standardisierten Knoten in Höhe von 100 GE (45+35+20) eingespart. Damit entstehen für die rechts unten abgebildete Konstellation Standardisierungskosten von 91 GE und kantenbezogene Kosten von 117 GE, d. h. die Gesamtkosten betragen 208 GE.

Komplexität des Standardisierungsproblems

Bei dem Standardisierungsproblem handelt es sich um ein Kombinatorisches Optimierungsproblem, bei dem sich die Komplexität im Trade-off zwischen den knotenbezogenen Standardisierungskosten und den kantenbezogenen Informationskosten begründet. Das Problem lässt sich mit Hilfe der linearen ganzzahligen Programmierung lösen. Dieses Lösungsverfahren wird insbesondere bei Erweiterungen des Standardisierungsproblems problematisch, da dann die Rechenzeiten stark ansteigen. Bei einer Erweiterung des Standardisierungsproblems um die Auswahl zwischen q alternativen Standards und T Perioden existieren bereits $(T+1)^{q^n}$ Lösungsmöglichkeiten, während das dargestellte einfache Standardisierungsproblem lediglich zu einer Komplexität von 2ⁿ Handlungsalternativen führt.

Aufgrund dieser Komplexität haben sich Wissenschaftler aus dem Gebiet des Operations Research mit dem Standardisierungsproblem beschäftigt und alternative Verfahren zur Ermittlung von Lösungen entwickelt. Kimms konzipiert einen Minimum-Cut-Ansatz, der dem ursprünglich entwickelten Branch-and-Bound-Verfahren in Bezug auf die Rechenzeit deutlich überlegen ist. Domschke/Wagner entwickeln weitere Lösungsverfahren und zeigen dabei, dass Probleme mit einem oder zwei Standards noch mit polynomialem Aufwand zu lösen sind. Probleme mit drei oder mehr Standards sind jedoch np-schwer.

Anwendungsbereiche und Erweiterungen

Obwohl das Standardisierungsproblem ursprünglich für das Gebiet der Kommunikationsstandards entwickelt wurde, ist es auf andere Domänen übertragbar. Wüstner erweitert das Standardisierungsproblem um die Einführung von Konvertern als Alternative zum Einsatz von Standards. Auf diese Weise lassen sich einerseits die Opportunitätskosten senken, die dadurch entstehen, dass nicht der Standard verwendet wird, der die Anforderungen am besten abdeckt. Andererseits führt diese Konverterlösung jedoch in der Regel zu höheren Kosten als die Verwendung von Standards, da die Integration von n Funktionen oder Bereichen zur Notwendigkeit des Einsatzes von bis zu $n \cdot (n-1)$ Konvertern führt (Wüstner 2005). Zudem sinkt durch den flächendeckenden Einsatz solcher Konvertierungslösungen in der Regel die Flexibilität der gesamten IT-Landschaft.

Durch Erweiterungen lässt es sich auf andere Domänen, wie z. B. den Einsatz von Standardsoftware oder die Nutzung von Diensten im Rahmen von serviceorientierten Plattformen, anwenden (Widjaja/Buxmann 2011).

Literatur

• Buxmann, P.: Standardisierung betrieblicher Informationssysteme, Wiesbaden 1996.
• Domschke, W.; G. Mayer und B. Wagner: Effiziente Modellierung von Entscheidungsproblemen: Das Beispiel des Standardisierungsproblems. Zeitschrift für Betriebswirtschaft 72 (2002), S. 847 - 863.
• Domschke, W. und B. Wagner: Models and Methods for Standardization Problems. European Journal of Operational Research 162 (2005), S. 713 - 726.
• Kimms, A.: Costing Communication Standards in Information Systems Using a Minimum Cut Approach. In: Journal of the Operational Research Society (2003) 54, S. 426-431.
• Widjaja, T. und Buxmann, P.: Kompatibilität von Softwareplattformen. Zeitschrift für Betriebswirtschaft (2011).
• Wüstner, E.: Standardisierung versus Konvertierung: Ökonomische Bewertung und Anwendung am Beispiel von XML/EDI (2005).