Cole-Cole-Kreis

Cole-Cole-Diagramm von Wasser bei 0 °C

Das Cole-Cole-Diagramm (auch: Cole-Cole-Kreis oder Cole-Cole-Plot) stellt komplexe Stoffparameter, wie Impedanzen oder die Permittivität von dielektrischen Materialien als Ortskurve in der gaußschen Zahlenebene als Funktion der Frequenz dar (siehe auch: Zeigerdiagramm). Es hat somit Ähnlichkeit zu dem (wenige Jahre später als Hilfsmittel für die HF-Technik entworfenen) Smith-Diagramm. Der Name des Cole-Cole-Diagramms stammt von den beiden Brüdern Kenneth S. Cole und Robert H. Cole, die um 1931 experimentelle Untersuchungen bezüglich der Impedanz von biologischem Gewebe durchführten.

Eigenschaften und Bedeutung

Ein typisches Cole-Cole-Diagramm beschreibt einen Halbkreis, dessen Mittelpunkt auf der reellen Achse liegt (siehe Bild). Auf der Abszisse des Cole-Cole-Diagramms wird der Realteil 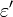$\varepsilon'$ der relativen Permittivität (Dielektrizitätszahl) 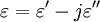$\varepsilon=\varepsilon'-j\varepsilon''$ und auf der Ordinate ihr negativer Imaginärteil 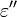$\varepsilon''$ (dielektrische Verluste) abgelesen.

Die relative Permittivität $\varepsilon$ von Stoffen hängt von der Temperatur und von der Frequenz ab. Die Frequenzabhängigkeit kann nach der folgenden Beziehung als Cole-Cole-Diagramm dargestellt werden, wobei ω die Kreisfrequenz und j die imaginäre Einheit ist.

$\varepsilon=\varepsilon_\infty+\frac{\varepsilon_s-\varepsilon_\infty}{1+{(j \omega \tau)^\alpha}}$

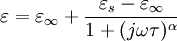
Als Ortskurve ergibt sich ein Halbkreis, dessen Lage und Größe von vier Parametern abhängt, die für das Beispiel von Wasser bei Raumtemperatur oder dem dielektrisch sehr ähnlichen Muskelgewebe etwa die folgenden Werte haben:

• Die statische Dielektrizitätszahl 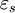$\varepsilon_s$, also die relative Permittivität des Dielektrikums bei der Frequenz 0 Hz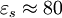 $\varepsilon_s \approx 80$
• Die Dielektrizitätszahl bei sehr hohen Frequenzen $\varepsilon_\infty \approx 6$
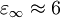
• Die Relaxationszeitkonstante $\tau \approx 10~ps$
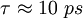
• Der Cole-Exponent, er beträgt für Muskelgewebe 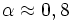$\alpha \approx 0,8$ und für Wasser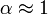 $\alpha \approx 1$

Dem Cole-Cole-Diagramm lassen sich einige wichtige charakteristische Parameter des untersuchten Dielektrikums entnehmen. Hierzu dienen der Cole-Exponent α, die Relaxationszeit τ beziehungsweise ihr Kehrwert ω_c = 1 / τ. Der Cole-Cole-Kreis weist zwei reelle Schnittpunkte mit der Abszisse auf. Bei der Resonanzfrequenz ω_c hat die Ortskurve ihr Maximum. Im Bild (oben) ist die Ortskurve der relativen Permittivität von Wasser für die Temperatur 0 °C dargestellt. Bei dieser Temperatur ist 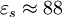$\varepsilon_s \approx 88$ und $\varepsilon_\infty \approx 4$.

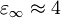Siehe auch

• Debye-Gleichung

Literatur

• Applikationsschrift der Firma Agilent: Basics of Measuring the Dielectric Properties of Materials. pp.13-19 PDF; 0,5 MB

Weblinks