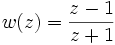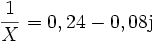Smithdiagramm

Das Smith-Diagramm (engl. Smith Chart) ist ein Hilfsmittel der komplexen Wechselstromrechnung, mit dem Berechnungen komplexer Widerstände (Impedanzen) auf eine geometrische Konstruktion zurückgeführt werden können. Es wurde im Jahre 1939 von Phillip Smith (1905–1987) entwickelt.

Darstellung der komplexen Reflexion eines Messobjektes im Smith-Diagramm nach Messung mit einem Netzwerkanalysator

Das Smith-Diagramm wird ebenfalls in der Leitungstheorie zur Impedanzanpassung verwendet. Das dort verwendete Smith-Diagramm unterscheidet sich lediglich durch die Interpretation der Achsen bzw. die Achsenbeschriftung von dem hier gezeigten.

In der Werkstofftechnik gibt es ebenfalls ein Smith-Diagramm (auch Dauerfestigkeitsschaubild genannt). Dieses hat nichts mit den o. g. Smith-Diagrammen zu tun, sondern beschreibt die Dauerfestigkeit von Werkstoffen. In diesem Diagramm werden die Scharen von Wöhlerlinien (beschreiben die Dauerfestigkeit für eine feste Mittelspannung) in Abhängigkeit von der Mittelspannung dargestellt. ^[1]

Aufbau

Smith-Diagramm

Das Diagramm ist kreisförmig und mit einem komplexen Koordinatensystem versehen. Es beruht auf der konformen Abbildung

$w(z) = {{z-1} \over {z+1}}$

der komplexen Ebene auf sich selbst. Sie ergibt sich aus der Definition des Reflexionsfaktors r.

Bei dieser Abbildung wird die rechte Halbebene auf das Innere des Einheitskreises abgebildet. Die linke Halbebene ist dabei ohne Bedeutung, da sie negativen ohmschen Widerständen entspricht, welche bei passiven Bauteilen nicht auftreten.

In der Mathematik ist diese Transformation einer Ebene in eine andere auch als Möbiustransformation bekannt. Sie gehorcht der allgemeinen Form

$f(z) = {az + b \over {cz + d}}$ .

Gauß-Ebene Smith-Diagramm

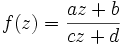Die Abbildung besitzt die besondere Eigenschaft, dass das Bild einer Zahl z (z. B. z = 2 + j) und ihres Kehrwertes (z. B. 1/z=1/(2+j)=0,4-0,2j) punktsymmetrisch zum Kreismittelpunkt liegen. (In der Elektrotechnik wird für die imaginäre Einheit das Symbol j verwendet, da das in der Mathematik hierfür übliche i mit dem Symbol für die Stromstärke verwechselt werden könnte.)

Das Smith-Diagramm kann somit sowohl als Impedanz- als auch Admittanz-Diagramm benutzt werden.

Bei der Berechnung einer Parallelschaltung ergibt sich der Kehrwert der Gesamtimpedanz als Summe der Kehrwerte der Teilimpedanzen. Diese Kehrwertbildung wird im Smith-Diagramm also geometrisch durch eine Spiegelung am Mittelpunkt ersetzt.

Im Smith-Diagramm wird immer mit normierten Größen gearbeitet. Daraus ergibt sich der Vorteil, dass man unabhängig von Größen wie der tatsächlichen Frequenz, Wellenlänge oder Impedanz ist.

In der Leitungstheorie, z. B. bei Impedanzanpassungsproblemen, lassen sich Reflexionsfaktor und Stehwellenverhältnis (SWR) einfach aus dem Smith-Diagramm ohne komplexe Rechnung bestimmen. Dazu misst man die Länge der Verbindungslinie zwischen dem Ursprung und dem Schnittpunkt der beiden Kreise der normierten Impedanz. Die Phase des Reflexionsfaktors kann auf der Verlängerung der Linie auf der äußeren Skala des Smith-Diagramms abgelesen werden. Das SWR lässt sich indirekt über den Reflexionsfaktor bestimmen, kann jedoch auch direkt aus dem Smith-Diagramm abgelesen werden – als Schnittpunkt der reellen Achse rechts vom Kreismittelpunkt mit dem Kreis, der durch den Betrag des Reflexionsfaktors gegeben ist.

Möchte man nun den Reflexionsfaktor an einer beliebigen Stelle auf einer Leitung berechnen, so entspricht dies einer Drehung des Reflexionsfaktors um die normierte Leitungslänge am Leitungsende auf dem Reflexionsfaktor-Kreis entweder hin zum Generator, also im Uhrzeigersinn, oder hin zur Last, also im Gegenuhrzeigersinn.

Das Smith-Diagramm bildet in der oberen Hälfte induktive und in der unteren Hälfte kapazitive Impedanzwerte ab.

Arbeiten mit dem Smith-Diagramm

• Normierung: Alle Elemente werden normiert, d. h. Impedanzen werden durch ihre charakteristische Impedanz Z₀ dividiert, Admittanzen mit Z₀ multipliziert und anschließend in das Smith-Diagramm eingetragen.

• In Serie geschaltete Impedanzen können direkt addiert werden
• Parallel geschaltete Impedanzen müssen zuerst auf Admittanz-Form gebracht werden, d. h. um den Mittelpunkt gespiegelt werden
• Stichleitung: Die Stichleitung ist in eine Ersatzimpedanz umzurechnen und je nach Anordnung wie eine serielle oder parallele Impedanz zu addieren
• Bewegung auf der Leitung: Impedanz-Diagramm oder Admittanz-Diagramm um die entsprechende Leitungslänge zum Generator (im Uhrzeigersinn) oder zur Last (im Gegenuhrzeigersinn) drehen.
• SWR: Das SWR erhält man, indem man den Punkt am gesuchten Ort um den Mittelpunkt auf die reelle Achse rechts dreht und den entsprechenden Wert abliest.
• Kurzschluss: Der Punkt ganz links im Impedanz-Diagramm, bzw. ganz rechts im Admittanz-Diagramm
• Leerlauf: Der Punkt ganz rechts im Impedanz-Diagramm, bzw. ganz links im Admittanz-Diagramm

Beispiel

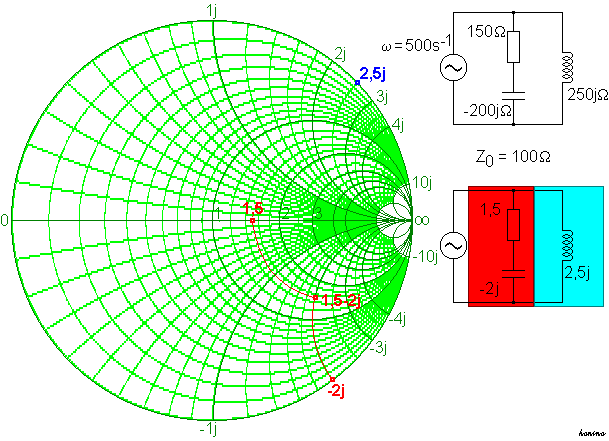
Ein ohmscher Widerstand R = 150 Ω und ein Kondensator C = 10 μF sind in Reihe geschaltet, parallel hierzu liegt eine Spule L = 0,5 H. Die Schaltung ist an einen Generator angeschlossen, dessen Frequenz f = 79,6 Hz beträgt.

Die Kreisfrequenz ist dann ω = 2πf = 500 s^-1.

Für den komplexen Widerstand (die Impedanz) des Kondensators folgt

$X_{\mathrm{C}} = {{1} \over {\mathrm{j} \omega C}} = - \mathrm{j} {{1} \over {\omega C}} = - 200 \mathrm{j}\ \Omega$,

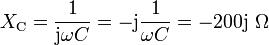für die Impedanz der Spule errechnet man

$X_{\mathrm{L}} = \mathrm{j} \omega L = 250 \mathrm{j}\ \Omega$.

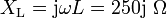Bei der Reihenschaltung aus Widerstand und Kondensator werden die Werte einfach addiert und ergeben

$X_1 = 150\ \Omega - 200 \mathrm{j}\ \Omega$.

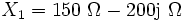Um die Werte ins Smith-Diagramm eintragen zu können, in dem sich große Zahlen nicht mehr darstellen lassen, normiert man mit einem geeigneten Bezugswiderstand, z. B. Z₀=100 Ω, indem man alle Werte durch ihn dividiert. Dann wird

X₁ = 1,5 − 2j (Widerstand und Kondensator)

und

X₂ = 2,5j (Spule).

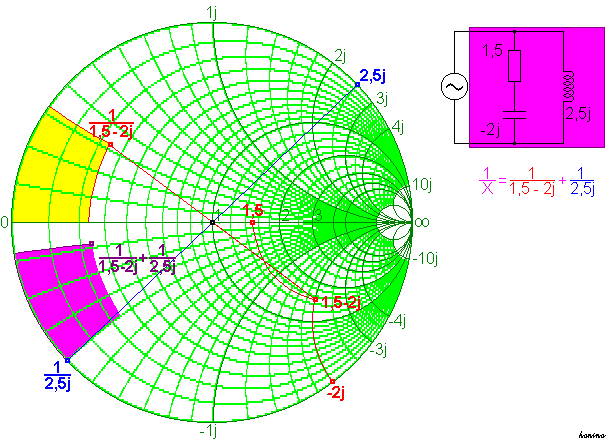
Diese beiden Widerstände sind parallel geschaltet. Für die Gesamtimpedanz X ist also

${1 \over X} = {1 \over X_1} + {1 \over X_2}$.

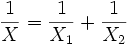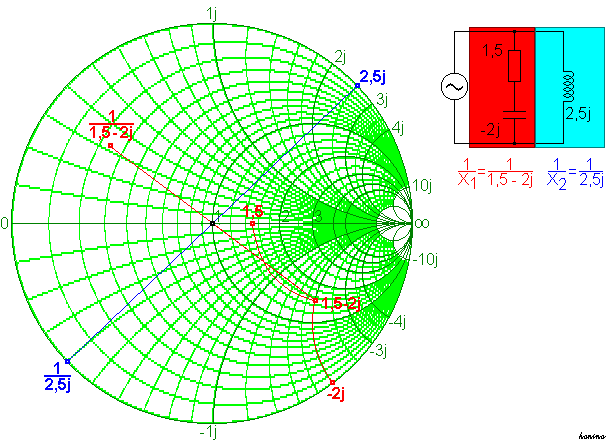
Diese Kehrwerte werden im Smith-Diagramm durch Spiegelung am Kreismittelpunkt gewonnen.

Sie betragen

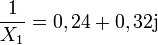${1 \over X_1} = 0,24 + 0,32 \mathrm{j}$ und ${1 \over X_2} = - 0,4 \mathrm{j}$ .

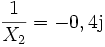Die Addition der beiden Kehrwerte erfolgt rechnerisch oder im Smith-Diagramm durch „Abzählen“ am Koordinatengitter.

Man erhält

${1 \over X} = 0,24 - 0,08 \mathrm{j}$

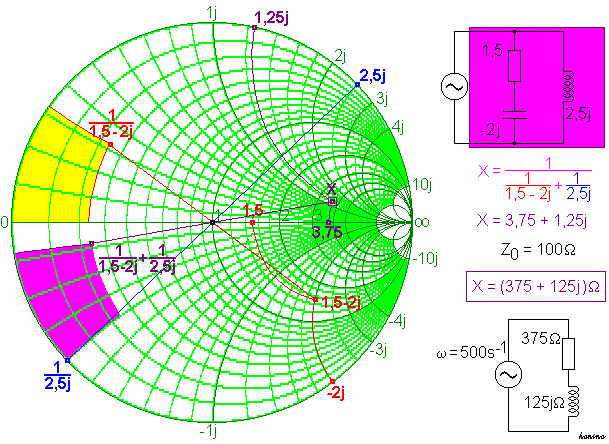
Um die Gesamtimpedanz X zu bestimmen, ist hiervon wieder der Kehrwert zu bilden. Man spiegelt also den soeben erhaltenen Punkt am Kreismittelpunkt wider.

Als Ergebnis findet man

X = 3,75 + 1,25j.

Da man zuvor durch 100 Ω dividiert hat, muss man nun wieder damit multiplizieren. Endgültig beträgt die Impedanz der Gesamtschaltung somit

X = 375 Ω + 125j Ω .

Sie kann daher ersatzweise durch eine Reihenschaltung aus einem Widerstand von 375 Ω und einer Spule von 125j Ω dargestellt werden (bei ω = 500 s^-1 entspricht das einer Induktivität von 0,25 H).

Einzelnachweise

1. ↑ Prof. Dr.-Ing. A. Jahr: Script zu Konstruktionslehre I, Kapitel 4.5. ([1] ; Version 02.01.1998). 

Siehe auch

• Zeigerdiagramm
• Bode-Diagramm
• Ortskurve
• Cole-Cole-Diagramm
• Netzwerkanalysator

Weblinks

• Smith Chart-Tool zur Impedanzanpassung (läuft im Browser)
• Smith-Diagramm als PDF
• Smith-Diagramm mit einstellbaren Parametern als PDF (A4 und US-Letter)
• Kurzanleitung zum Smith-Diagramm (PDF)
• Java-Programm zur Darstellung von Smith-Diagrammen, frei erhältlich, lauffähig auch unter Linux
• LinSmith – Smith-Diagramme unter Linux
• Demo-Version eines Programmes zur Darstellung von Smith-Diagrammen
• Ein Matlab-Programm zur Erzeugung eines Standard-Smith-Diagramms.