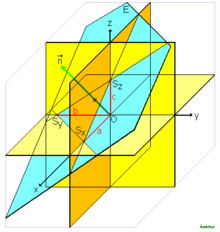
Achsenabschnittsform

Die Achsenabschnittsform einer Ebene ist eine Gleichung, die diese Ebene mittels ihrer Achsenabschnitte auf den Koordinatenachsen beschreibt. Wenn a, b und c die Abschnitte auf der x-Achse, y-Achse und z-Achse sind, so lautet die Achsenabschnittsform:

${x \over a} + {y \over b} + {z \over c} = 1$.

Achsenabschnittsform

Anwendung findet diese Geradenform z.B. bei den Millerschen Indizes.

Im zweidimensionalen Raum gibt es auch die Achsenabschnittsform der Geradengleichung.

Erklärung

Die Achsenabschnittsform der Ebene kann man aus der Normalform herleiten. Mit einem Normalenvektor $\vec n$ gilt für jeden Ortsvektor $\vec r$, der zu einem Punkt P der Ebene gehört:

$\vec r \cdot \vec n = k$

mit einer Konstanten k. Die Spurpunkte S_x, S_y und S_z haben insbesondere die Ortsvektoren

$\begin{pmatrix} a \\ 0 \\ 0 \end{pmatrix}$,$\begin{pmatrix} 0 \\ b \\ 0 \end{pmatrix}$ und $\begin{pmatrix} 0 \\ 0 \\ c \end{pmatrix}$.

Wenn $\vec n = \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix}$ ist, folgt also:

$k = \begin{pmatrix} a \\ 0 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} = \begin{pmatrix} 0 \\ b \\ 0 \end{pmatrix} \cdot \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ c \end{pmatrix} \cdot \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix}$,

d. h.

$k = a \cdot n_x = b \cdot n_y = c \cdot n_z$

und daher

${1 \over a} = {n_x \over k}$, ${1 \over b} = {n_y \over k}$ und ${1 \over c} = {n_z \over k}$.

Indem man nun die Normalform

$\vec x \cdot \vec n = \begin{pmatrix} x \\ y \\ z \end{pmatrix} \cdot \begin{pmatrix} n_x \\ n_y \\ n_z \end{pmatrix} = k$

durch k dividiert, erhält man

$\begin{pmatrix} x \\ y \\ z \end{pmatrix} \cdot \begin{pmatrix} {n_x \over k} \\ {n_y \over k} \\ {n_z \over k} \end{pmatrix} = 1$,

ausmultipliziert:

$x \cdot {n_x \over k} + y \cdot {n_y \over k} + z \cdot {n_z \over k} = 1$,

und folglich die Achsenabschnittsform:

${x \over a} + {y \over b} + {z \over c} = 1$.

Ausnahmen und Sonderfälle

Die Achsenabschnittsform existiert nicht, falls die Ebene durch den Koordinatenursprung verläuft. In diesem Falle werden alle Achsenabschnitte zugleich 0, und in der Normalform wird k = 0, sodass die Division durch k unmöglich ist.

Verläuft die Ebene parallel zu einer oder zu zwei Koordinatenachsen, so fallen ein oder zwei Spurpunkte weg, und damit fällt der betreffende Term in der Achsenabschnittsform weg. Eine Ebene, die parallel zur y-Achse verläuft, hat z. B. keinen Achsenabschnitt b, und es verbleibt nur

${x \over a} + {z \over c} = 1$.

Beispiel

Eine Ebene hat den Normalenvektor

$\vec n = \begin{pmatrix} 4 \\ -3 \\ 6 \end{pmatrix}$

und verläuft durch den Punkt P(3|2|1). Ihre Normalform lautet also:

$\vec r \cdot \begin{pmatrix} 4 \\ -3 \\ 6 \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 4 \\ -3 \\ 6 \end{pmatrix} = 4 \cdot 3 - 3 \cdot 2 + 6 \cdot 1 = 12$.

Division durch 12 liefert:

$\vec r \cdot \begin{pmatrix} {4 \over 12} \\ {-3 \over 12}\\ {6 \over 12}\end{pmatrix} = 1$,

also ergibt sich mit $\vec r = \begin{pmatrix} x \\ y \\ z \end{pmatrix}$,

${x \over 3} + {y \over -4} + {z \over 2} = 1$.