Cournotpunkt

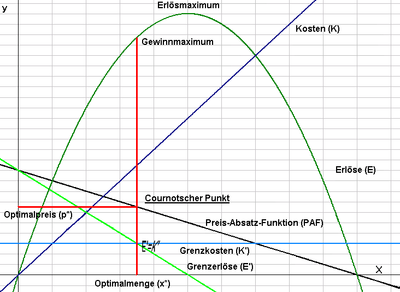
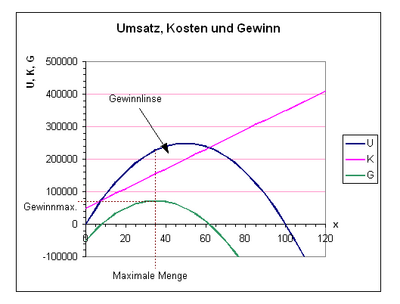
Der cournotsche Punkt ist das nach dem französischen Wirtschaftswissenschaftler Antoine Augustin Cournot (* 1801; † 1877) benannte Gewinnmaximum eines Monopolunternehmens. Er errechnet sich aus einer verkauften Menge zu einem verlangten Preis eines Produktes minus den Produktionskosten. Typisch für den cournotschen Punkt ist, dass das Gewinnmaximum vor dem Umsatzmaximum erreicht wird.

Berechnung des cournotschen Punkts (C) mit gewinnmaximalem Preis (p_c) und gewinnmaximaler Absatzmenge (x_c):

cournotscher Punkt graphisch

Im Gegensatz zum Unternehmen im vollkommenen Wettbewerb, das für sein Produkt einen Marktpreis akzeptieren muss, kann der Monopolist den Verkaufspreis gewinnmaximierend festsetzen. Er muss dafür eine Nachfragefunktion, d. h. zu welchem Preis er wie viel von dem Produkt absetzen kann, annehmen oder sich langsam mit seiner Preispolitik dem Gewinnoptimum nähern (Cobweb-Theorem). Bei Oligopolisten oder Kartellmitgliedern gelten Preis-/Absatzkurven, die sich stark am Preisverhalten der wenigen Mitanbieter orientieren.

x = x(p),

bzw. als Umkehrfunktion die Preis-Absatz-Funktion als

p = p(x).

Daraus bestimmt sich der Gesamterlös (oft E, hier Umsatz U) als Preis × Menge

U(x) = p(x)x.

Mit der Gesamtkostenfunktion K(x) erzielt das Unternehmen den Gewinn G(x) als

G(x) = U(x) − K(x).

Um den maximalen Gewinn zu ermitteln, wird die erste Ableitung von G(x) gebildet (d. h. G'(x)) und gleich Null gesetzt. Die ermittelten Nullstellen (bei S-förmigem Kostenverlauf oder anderen nicht linearen Gewinnverläufen) müssen nun in die zweite Ableitung eingesetzt werden. Die Nullstelle, bei der diese zweite Ableitung negativ ist, ist die gewinnmaximale Ausbringungsmenge x_c, die den cournotschen Punkt definiert. Um nun den cournotschen Punkt zu erhalten, wird der zu x_c gehörende Preis p_c aus der Preis-Absatz-Funktion ermittelt.

Da man beim Maximieren der Gewinnfunktion wegen

G'(x) = U'(x) − K'(x) = 0

auch

U'(x) = K'(x)

schreiben kann, folgt, dass sich der cournotsche Punkt auch berechnen lässt, indem man direkt die Grenzkosten K'(x) dem Grenzerlös U'(x) gleichsetzt. Der x-Wert des Schnittpunkts bildet die gewinnmaximale Absatzmenge x_c. Dieser muss in die Preis-Absatz-Funktion eingesetzt werden, um den gewinnmaximalen Preis p_c zu bestimmen. Gewinnmaximale Absatzmenge und zugehöriger Preis bilden zusammen den cournotschen Punkt.

Beispiel

Absolute Werte graphisch

Ein monopolistisch agierendes Unternehmen produziert extraleichte Trekkingschuhe. Diese werden in größeren Gebinden an Weiterverkäufer geliefert. Die Vertriebsleitung hat festgestellt, dass die Nachfrage x [Stück Gebinde] nach diesen Schuhen vom Preis p [Geldeinheiten (GE)] abhängt, und zwar mit der Nachfragefunktion

x = x(p) = 100 − 0,01p.

Umgekehrt ergibt sich die Preis-Absatz-Funktion (Nachfragefunktion abhängig von x) als

p = p(x) = 10.000 − 100x.

D. h. dass er bei einem Preis von 10.000 GE kein Paar mehr verkauft (Prohibitivpreis) und trotz eines Preises von 0 GE nicht mehr als 100 Paare verkauft (Sättigungsmenge).

Bewertet man die nachgefragte Menge x mit dem jeweilig gültigen Preis, erhält man den Umsatz als Funktion

U = U(x) = xp(x) = 10.000x − 100x².

Dem Unternehmen entstehen durch die Produktion der Trekkingschuhe Gesamtkosten, die von der Ausbringungsmenge x [Stück Gebinde] abhängig sind. Die Kosten des Unternehmens lassen sich in der Kostenfunktion

K = K(x) = 50.000 + 3.000x.

zusammenfassen. Der Gewinn berechnet sich dann als Umsatz – Kosten, also

G = G(x) = U(x) − K(x) = 10.000x − 100x² − 50.000 − 3.000x,

so dass man als Gewinnfunktion

G(x) = 7.000x − 100x² − 50.000

erhält.

Um das Gewinnmaximum im cournotschen Punkt zu erhalten, bestimmt man das Maximum der Gewinnfunktion durch Differenzieren von G(x):

$\frac {dG}{dx}= 7.000-200x$.

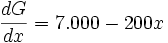Das Nullsetzen der Ableitung ergibt dann die Lösung: x_c=35 und G_c=72.500.

Da die zweite Ableitung

G'' = − 200

kleiner als Null ist, handelt es sich bei der Lösung um ein Gewinnmaximum.

Zur cournotschen Menge

x_c = 35

gehört der cournotsche Preis

p(x)=10000-100x

p(35)=10000-100*35

p_c = 6500.

Zum Preis von 6500 GE können also 35 Gebinde Schuhe verkauft werden. Damit erzielt das Unternehmen 72.500 GE Gewinn. ((10.000*35-100*35*35)-(50.000+3.000*35))

Die allgemeine Lösung der Gewinnoptimierung bei Wettbewerb sowie bei begrenzter Kapazität findet sich in [Gudehus 2007]. Wenn zur Kapazitätssteigerung investiert werden muss, sind auch die Fixkosten bei der Berechnung des absoluten Cournot-Punktes zu berücksichtigen.

Literatur

• Gudehus T.:Dynamische Märkte, Praxis, Strategien und Nutzen für Wirtschaft und Gesellschaft, s. 12.4 Gewinnmaximierung und 12.5 Cournotscher Punkt, Springer, Berlin-Heidelberg-New York, 2007, ISBN 978-3-540-72597-8

Siehe auch

• Formelsammlung Mikroökonomie