D'Alembert-Differentialgleichung
- D'Alembert-Differentialgleichung
-
Die d’Alembertsche Differentialgleichung, auch lagrangesche Differentialgleichung genannt, ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form
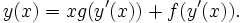
Sie ist nach Jean-Baptiste le Rond d’Alembert benannt. Ein Sonderfall dieser Differentialgleichung ist die clairautschen Differentialgleichung.
Formulierung
Sei 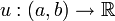 eine Lösung der Gleichung
eine Lösung der Gleichung
![\ [x-g(x)]u'(x) - g'(x)u(x) = f'(x)](/pictures/dewiki/53/50ef009f6e420ea4f5afd77e6311e19f.png)
und u auf (a,b) injektiv mit differenzierbarer Umkehrfunktion u − 1. Dann ist
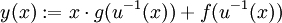
eine Lösung der d’Alembertschen Differentialgleichung.
Beweis
Es gilt:
![\begin{array}{lll}
y'(x)&=&g(u^{-1}(x))+\frac{xg'(u^{-1}(x)) + f'(u^{-1}(x))}{u'(u^{-1}(x))}\\
&=&g(u^{-1}(x))+\frac{xg'(u^{-1}(x)) + [u^{-1}(x)-g(u^{-1}(x))]u'(u^{-1}(x)) - xg'(u^{-1}(x))}{u'(u^{-1}(x))}\\
&=&u^{-1}(x)\ .\end{array}](/pictures/dewiki/53/5ce2372552c07d1306d6f98665179f5d.png)
Man beachte allerdings, dass man auf diese Weise im Allgemeinen nicht alle Lösungen findet, wie man schon im Spezialfall der clairautschen Differentialgleichung sieht. Dort würde man mit diesem Verfahren nur die dort als nichttriviale Lösungen bezeichneten Lösungen finden.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Reduktionsverfahren von d'Alembert — Das Reduktionsverfahren von d’Alembert ist ein Verfahren aus der Theorie gewöhnlicher Differentialgleichungen. Es wird verwendet, um eine lineare Differentialgleichung n ter Ordnung mit nicht konstanten Koeffizienten unter Kenntnis einer (ggf.… … Deutsch Wikipedia
Reduktionsverfahren von d’Alembert — Das Reduktionsverfahren von d’Alembert ist ein Verfahren aus der Theorie gewöhnlicher Differentialgleichungen. Es wird verwendet, um eine lineare Differentialgleichung n ter Ordnung mit nicht konstanten Koeffizienten unter Kenntnis einer (ggf.… … Deutsch Wikipedia
D'Alembertsche Differentialgleichung — Die d’Alembertsche Differentialgleichung, auch lagrangesche Differentialgleichung genannt, ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form Sie ist nach Jean Baptiste le Rond d’Alembert benannt. Ein Sonderfall… … Deutsch Wikipedia
D’Alembertsche Differentialgleichung — Die d’Alembertsche Differentialgleichung, auch lagrangesche Differentialgleichung genannt, ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form Sie ist nach Jean Baptiste le Rond d’Alembert benannt. Ein Sonderfall… … Deutsch Wikipedia
d’Alembertsche Differentialgleichung — Die d’Alembertsche Differentialgleichung, auch lagrangesche Differentialgleichung genannt, ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form Sie ist nach Jean Baptiste le Rond d’Alembert benannt. Ein Sonderfall… … Deutsch Wikipedia
Hauptvektorlösung — Als Fundamentalsystem bezeichnet man in der Analysis jede Basis des Vektorraums, der aus der Menge der Lösungen eines homogenen linearen gewöhnlichen Differentialgleichungssystems gebildet wird. Ist ein Fundamentalsystem, so ist definitionsgemäß… … Deutsch Wikipedia
D'Alembertsches Reduktionsverfahren — Das Reduktionsverfahren von d’Alembert ist ein Verfahren aus der Theorie gewöhnlicher Differentialgleichungen. Es wird verwendet, um eine lineare Differentialgleichung n ter Ordnung mit nicht konstanten Koeffizienten unter Kenntnis einer (ggf.… … Deutsch Wikipedia
Reduktionsverfahren — Das Reduktionsverfahren von d’Alembert ist ein Verfahren aus der Theorie gewöhnlicher Differentialgleichungen. Es wird verwendet, um eine lineare Differentialgleichung n ter Ordnung mit nicht konstanten Koeffizienten unter Kenntnis einer (ggf.… … Deutsch Wikipedia
Laplace — Gemälde aus dem 19. Jahrhundert Kupferstich aus dem 19. Jahrhundert Pierre Simon (Marquis de) Laplace (* 28. März 1749[1 … Deutsch Wikipedia
Pierre-Simon Marquis de Laplace — Gemälde aus dem 19. Jahrhundert Kupferstich aus dem 19. Jahrhundert Pierre Simon (Marquis de) Laplace (* 28. März 1749[1 … Deutsch Wikipedia
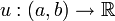 eine Lösung der Gleichung
eine Lösung der Gleichung

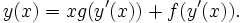
![\ [x-g(x)]u'(x) - g'(x)u(x) = f'(x)](/pictures/dewiki/53/50ef009f6e420ea4f5afd77e6311e19f.png)
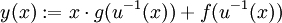
![\begin{array}{lll}
y'(x)&=&g(u^{-1}(x))+\frac{xg'(u^{-1}(x)) + f'(u^{-1}(x))}{u'(u^{-1}(x))}\\
&=&g(u^{-1}(x))+\frac{xg'(u^{-1}(x)) + [u^{-1}(x)-g(u^{-1}(x))]u'(u^{-1}(x)) - xg'(u^{-1}(x))}{u'(u^{-1}(x))}\\
&=&u^{-1}(x)\ .\end{array}](/pictures/dewiki/53/5ce2372552c07d1306d6f98665179f5d.png)