D’Alembertsche Differentialgleichung
- D’Alembertsche Differentialgleichung
-
Die d’Alembertsche Differentialgleichung, auch lagrangesche Differentialgleichung genannt, ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form
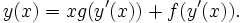
Sie ist nach Jean-Baptiste le Rond d’Alembert benannt. Ein Sonderfall dieser Differentialgleichung ist die clairautschen Differentialgleichung.
Formulierung
Sei 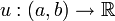 eine Lösung der Gleichung
eine Lösung der Gleichung
![\ [x-g(x)]u'(x) - g'(x)u(x) = f'(x)](/pictures/dewiki/53/50ef009f6e420ea4f5afd77e6311e19f.png)
und u auf (a,b) injektiv mit differenzierbarer Umkehrfunktion u − 1. Dann ist
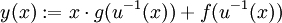
eine Lösung der d’Alembertschen Differentialgleichung.
Beweis
Es gilt:
![\begin{array}{lll}
y'(x)&=&g(u^{-1}(x))+\frac{xg'(u^{-1}(x)) + f'(u^{-1}(x))}{u'(u^{-1}(x))}\\
&=&g(u^{-1}(x))+\frac{xg'(u^{-1}(x)) + [u^{-1}(x)-g(u^{-1}(x))]u'(u^{-1}(x)) - xg'(u^{-1}(x))}{u'(u^{-1}(x))}\\
&=&u^{-1}(x)\ .\end{array}](/pictures/dewiki/53/5ce2372552c07d1306d6f98665179f5d.png)
Man beachte allerdings, dass man auf diese Weise im Allgemeinen nicht alle Lösungen findet, wie man schon im Spezialfall der clairautschen Differentialgleichung sieht. Dort würde man mit diesem Verfahren nur die dort als nichttriviale Lösungen bezeichneten Lösungen finden.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
D'Alembertsche Differentialgleichung — Die d’Alembertsche Differentialgleichung, auch lagrangesche Differentialgleichung genannt, ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form Sie ist nach Jean Baptiste le Rond d’Alembert benannt. Ein Sonderfall… … Deutsch Wikipedia
d’Alembertsche Differentialgleichung — Die d’Alembertsche Differentialgleichung, auch lagrangesche Differentialgleichung genannt, ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form Sie ist nach Jean Baptiste le Rond d’Alembert benannt. Ein Sonderfall… … Deutsch Wikipedia
Gewöhnliche Differentialgleichung — Eine gewöhnliche Differentialgleichung (oft abgekürzt mit ODE, englisch ordinary differential equation) ist eine Differentialgleichung, bei der zu einer gesuchten Funktion nur Ableitungen nach genau einer Variablen auftreten. Viele… … Deutsch Wikipedia
D'Alembert-Differentialgleichung — Die d’Alembertsche Differentialgleichung, auch lagrangesche Differentialgleichung genannt, ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form Sie ist nach Jean Baptiste le Rond d’Alembert benannt. Ein Sonderfall… … Deutsch Wikipedia
Gewöhnliche Differentialgleichungen — Eine gewöhnliche Differentialgleichung (oft abgekürzt mit ODE, englisch ordinary differential equation) ist eine Differentialgleichung, bei der zu einer gesuchten Funktion nur Ableitungen nach genau einer Variablen auftreten. Viele… … Deutsch Wikipedia
Gewöhnliche Differenzialgleichung — Eine gewöhnliche Differentialgleichung (oft abgekürzt mit ODE, englisch ordinary differential equation) ist eine Differentialgleichung, bei der zu einer gesuchten Funktion nur Ableitungen nach genau einer Variablen auftreten. Viele… … Deutsch Wikipedia
Clairaut-Gleichung — Die clairautsche Differentialgleichung ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form und ist somit ein Spezialfall der d Alembertschen Differentialgleichung. Sie ist nach dem französischen Mathematiker Alexis… … Deutsch Wikipedia
Lagrange-Funktion — Die Lagrange Funktion (nach Joseph Louis Lagrange) ist ein zentrales Element zur Beschreibung von physikalischen Systemen im Lagrange Formalismus der Klassischen Mechanik. Für konservative Systeme sowie für nicht konservative Systeme mit einem… … Deutsch Wikipedia
Lagrange-Gleichung — Die Lagrange Funktion (nach Joseph Louis Lagrange) ist ein zentrales Element zur Beschreibung von physikalischen Systemen im Lagrange Formalismus der Klassischen Mechanik. Für konservative Systeme sowie für nicht konservative Systeme mit einem… … Deutsch Wikipedia
Lagrangefunktion — Die Lagrange Funktion (nach Joseph Louis Lagrange) ist ein zentrales Element zur Beschreibung von physikalischen Systemen im Lagrange Formalismus der Klassischen Mechanik. Für konservative Systeme sowie für nicht konservative Systeme mit einem… … Deutsch Wikipedia
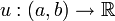 eine Lösung der Gleichung
eine Lösung der Gleichung

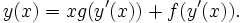
![\ [x-g(x)]u'(x) - g'(x)u(x) = f'(x)](/pictures/dewiki/53/50ef009f6e420ea4f5afd77e6311e19f.png)
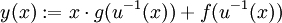
![\begin{array}{lll}
y'(x)&=&g(u^{-1}(x))+\frac{xg'(u^{-1}(x)) + f'(u^{-1}(x))}{u'(u^{-1}(x))}\\
&=&g(u^{-1}(x))+\frac{xg'(u^{-1}(x)) + [u^{-1}(x)-g(u^{-1}(x))]u'(u^{-1}(x)) - xg'(u^{-1}(x))}{u'(u^{-1}(x))}\\
&=&u^{-1}(x)\ .\end{array}](/pictures/dewiki/53/5ce2372552c07d1306d6f98665179f5d.png)