- Adaptierter Prozess
-
Der Begriff Filtrierung (auch Filtration, Filterung oder Filtern) bezeichnet in der Theorie der stochastischen Prozesse eine Familie von verschachtelten σ-Algebren, welche die zu verschiedenen Zeitpunkten verfügbare Information über den Verlauf von zufälligen Prozessen modelliert.
Inhaltsverzeichnis
Definition
Sei T eine beliebige geordnete Indexmenge und
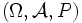 ein Wahrscheinlichkeitsraum.
ein Wahrscheinlichkeitsraum.Eine Familie
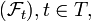 von σ-Algebren heißt Filtrierung, falls
von σ-Algebren heißt Filtrierung, falls 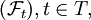 aufsteigend geordnet ist, das heißt, dass für alle
aufsteigend geordnet ist, das heißt, dass für alle 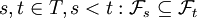 gilt.
gilt.Eine alternative Definition fordert zusätzlich, dass die Familie der σ-Algebra rechtsseitig stetig ist, dass also gilt:
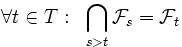 .
.
Ein stochastischer Prozess
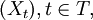 heißt an die Filtrierung
heißt an die Filtrierung 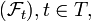 angepasst (oder adaptiert), wenn Xt stets
angepasst (oder adaptiert), wenn Xt stets 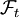 -messbar ist für alle t.
-messbar ist für alle t.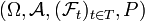 heißt gefilterter Wahrscheinlichkeitsraum, wenn die
heißt gefilterter Wahrscheinlichkeitsraum, wenn die 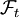 Sub-σ-Algebren von
Sub-σ-Algebren von  sind.
sind.Verwendung des Begriffes
Der Begriff der Filtrierung ist unerlässlich, um, ausgehend vom Begriff des stochastischen Prozesses, wichtige Begriffe wie Martingale oder Stoppzeiten einzuführen.
Als Menge T wird wie bei stochastischen Prozessen meist
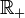 oder
oder 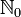 gewählt und
gewählt und 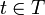 als Zeitpunkt interpretiert.
als Zeitpunkt interpretiert.σ-Algebren modellieren verfügbare Information. Die Mengen der σ-Algebra
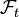 geben zu jedem Zeitpunkt t an, wie viele Informationen zur Zeit bekannt sind. Für jedes Ereignis
geben zu jedem Zeitpunkt t an, wie viele Informationen zur Zeit bekannt sind. Für jedes Ereignis 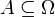 bedeutet
bedeutet 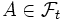 übersetzt, dass zum Zeitpunkt t die Frage „ist
übersetzt, dass zum Zeitpunkt t die Frage „ist 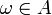 ?“ eindeutig mit „ja“ oder „nein“ beantwortet werden kann. Dass die Filtrierung stets aufsteigend geordnet ist, bedeutet demnach, dass eine einmal erlangte Information nicht mehr verloren geht.
?“ eindeutig mit „ja“ oder „nein“ beantwortet werden kann. Dass die Filtrierung stets aufsteigend geordnet ist, bedeutet demnach, dass eine einmal erlangte Information nicht mehr verloren geht.Ist ein stochastischer Prozess
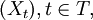 an eine Filtrierung
an eine Filtrierung 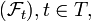 adaptiert, bedeutet dies also, dass der Verlauf der Funktion
adaptiert, bedeutet dies also, dass der Verlauf der Funktion 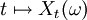 im Intervall [0,t] zum Zeitpunkt t (für beliebiges, aber unbekanntes
im Intervall [0,t] zum Zeitpunkt t (für beliebiges, aber unbekanntes 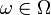 und in Hinsicht auf die durch Ereignisse
und in Hinsicht auf die durch Ereignisse ![A \in \mathcal F_s, s \in [0,t]](/pictures/dewiki/102/ff070660beca9cd8bf49e4d397a679fc.png) formulierbaren Fragen) bekannt ist.
formulierbaren Fragen) bekannt ist.Der Begriff wird aufgrund seiner Bedeutung in den meisten fortgeschrittenen Lehrbüchern über stochastische Prozesse definiert. In einigen Lehrbüchern, zum Beispiel im Buch Probability von Albert N. Schirjajew, wird der Begriff aus didaktischen Gründen zunächst umfassend für Prozesse mit diskreten Werten in diskreter Zeit eingeführt.
Beispiele
- Natürliche Filtrierung: Ist
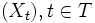 ein stochastischer Prozess, so wird das durch
ein stochastischer Prozess, so wird das durch 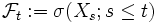 erzeugte System als natürliche Filtrierung des Prozesses bezeichnet (σ bezeichnet dabei den σ-Algebren-Operator). Es ist also zu jedem Zeitpunkt t die vollständige Information über den vergangenen Verlauf des Prozesses bis einschließlich zum Zeitpunkt t vorhanden.
erzeugte System als natürliche Filtrierung des Prozesses bezeichnet (σ bezeichnet dabei den σ-Algebren-Operator). Es ist also zu jedem Zeitpunkt t die vollständige Information über den vergangenen Verlauf des Prozesses bis einschließlich zum Zeitpunkt t vorhanden.
- Filtrierung der vollständigen Information: Durch
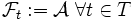 wird die Filtrierung der vollständigen Information definiert. Hier ist also zu jedem Zeitpunkt t die vollständige Information vorhanden.
wird die Filtrierung der vollständigen Information definiert. Hier ist also zu jedem Zeitpunkt t die vollständige Information vorhanden.
Spezielle Eigenschaften
Die zur Filtrierung
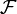 gehörende terminale σ-Algebra erfüllt
gehörende terminale σ-Algebra erfüllt 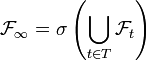 .
.Zu einem beliebigen Zeitpunkt
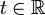 definiert man als linken Grenzwert der Filtrierung die σ-Algebra
definiert man als linken Grenzwert der Filtrierung die σ-Algebra 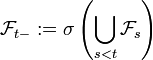 .
.
Dabei gilt stets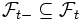 . Stimmen Filtrierung und linker Grenzwert zu jedem Zeitpunkt überein, so heißt die Filtrierung linksseitig stetig. Eine stetige Filtrierung ist konsequenterweise eine solche, die links- und rechtsseitig stetig ist.
. Stimmen Filtrierung und linker Grenzwert zu jedem Zeitpunkt überein, so heißt die Filtrierung linksseitig stetig. Eine stetige Filtrierung ist konsequenterweise eine solche, die links- und rechtsseitig stetig ist.Literatur
- Daniel Revuz, Marc Yor: Continuous Martingales and Brownian motion. Springer-Verlag, New York 1999, ISBN 3-540-64325-7.
- A. N. Shiryayev: Probability. Springer-Verlag, New York 1984, ISBN 3-540-90898-6.
Wikimedia Foundation.
