Denotationsfunktion

Ein Wahrheitswert (logischer Wert) gibt in der Logik den Grad der Wahrheit eines Satzes an. Gibt es in einem logischen System mehr als zwei Wahrheitswerte, spricht man oft lieber von Quasiwahrheitswerten, Pseudowahrheitswerten oder Geltungswerten. Unter einer Wahrheitswertzuordnung (synonym: Wahrheitsfunktion, Wahrheitswertefunktion, Denotationsfunktion oder Bewertungsfunktion) versteht man eine Funktion im mathematischen Sinn, die die Menge der Aussagen einer (meist formalen) Sprache auf die Menge ihrer Wahrheitswerte abbildet.

Eingeführt wurde der Begriff „Wahrheitswert“ von Gottlob Frege als undefinierter Grundbegriff, unter den die beiden Gegenstände fallen, die nach seiner Sicht als Werte von Wahrheitswertefunktion auftreten können – das Wahre und das Falsche: „Ich verstehe unter dem Wahrheitswerthe eines Satzes den Umstand, daß er wahr oder daß er falsch ist.“^[1] Auf der Basis der Unterscheidung zwischen Extension und Intension wird im Gefolge von Frege vielfach angenommen, dass der Wahrheitswert die Extension (das Designat, die Referenz, in Freges Terminologie die Bedeutung) einer Aussage ist.

Nach dem gängigen Verständnis haben nur Aussagesätze Wahrheitswerte, nicht aber zum Beispiel Fragesätze oder einzelne Wörter. Der Begriff des Wahrheitswertes ist nicht an eine bestimmte Wahrheitstheorie gebunden.

Anzahl der Wahrheitswerte

In der klassischen, zweiwertigen Logik hat jeder Satz einen von genau zwei Wahrheitswerten: Er ist entweder wahr oder falsch. Man nennt diesen Sachverhalt auch das Prinzip der Zweiwertigkeit.

In mehrwertigen Logiken gibt es mehr als zwei Wahrheitswerte, das heißt das Prinzip der Zweiwertigkeit wird aufgegeben. Der Satz vom ausgeschlossenen Dritten wird dadurch jedoch nicht automatisch mit aufgegeben – vielmehr gibt es mehrwertige Logiken, in denen der Satz vom ausgeschlossenen Dritten gilt, und solche, in denen er nicht gilt.

Es gibt Logiken mit endlich vielen Wahrheitswerten, so zum Beispiel das als erste mehrwertige Logik 1920 von Jan Łukasiewicz formalisierte System Ł₃, eine dreiwertige Logik. Es gibt aber auch Logiken mit unendlich vielen Wahrheitswerten, zum Beispiel Fuzzy-Logik.

Extensionalität und Wahrheitsfunktionalität

In extensionalen Logiken ist der Wahrheitswert eines zusammengesetzten Satzes eindeutig aus den Wahrheitswerten seiner Teilsätze bestimmt (Prinzip der Wahrheitsfunktionalität, allgemeiner: Extensionalitätsprinzip oder Kompositionalitätsprinzip); man sagt auch: Die Junktoren (Konnektive) sind wahrheitsfunktional. Die klassische Logik verwendet ausschließlich wahrheitsfunktionale Konnektive, ist also extensional. Zur Angabe des Wahrheitswertverlaufs eines extensionalen (wahrheitsfunktionalen) Konnektivs werden in endlichwertigen Logiken gerne Wahrheitstabellen verwendet.

In intensionalen Logiken, das heißt in solchen, die auch (oder nur) Konnektive enthalten, die nicht wahrheitsfunktional sind, sind die Formalismen erheblich aufwendiger und diverser, mit denen man den Wahrheitswert eines komplexen Satzes berechnet. Für manche intensionale Logiken, vor allem für Modallogik, hat sich die Kripke-Semantik zur Bewertung von Sätzen bewährt.

Symbole für Wahrheitswerte

Die Wahrheitswerte werden unterschiedlich symbolisiert; gebräuchlich sind folgende Zeichen:

wahr

„W“ (wahr), „t“ (englisch „true“), „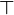$\top$“, "v" (lateinisch verum), „1“ oder „+“.

falsch

„F“ (falsch), „f“ (englisch „false“), „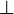$\bot$“, „0“ oder „–“.

In einer mehrwertigen Logik greift man entweder auf Zahlen zurück, die einen abgestuften Wahrheitsgrad beschreiben z.B. 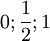${0; \frac{1}{2}; 1}$ in dreiwertigen Logik auf oder 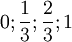${0; \frac{1}{3}; \frac{2}{3}; 1}$ in einer vierwertigen Logik (vergleiche Wahrheitstabelle) oder auch auf alle reellen Zahlen zwischen 0 ond 1 (vergleiche Fuzzy Logik). Andererseits sind auch Wahrheitswerte wie "undefiniert", "indifferent" oder "hochohmig" gebräuchlich.

Einzelnachweise

1. ↑ Über Sinn und Bedeutung, Seite 34

Literatur

• L. Kreiser, S. Gottwald, W. Stelzner (Hge): Nichtklassische Logik. Eine Einführung, Berlin: Akademie ²1990
• Tugendhat/Wolf, Logisch-semantische Propädeutik, 1983. ISBN 3150082064

Siehe auch

• Funktion und Begriff
• Über Sinn und Bedeutung