- Dirichlet'sche Eta-Funktion
-
In der Zahlentheorie ist die dirichletsche η-Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805−1859) benannt ist. Sie ist verwandt mit der riemannschen ζ-Funktion.
Sie wird mit dem kleinen griechischen Buchstaben eta (η) notiert; die dedekindsche η-Funktion, eine Modulform, wird aber ebenfalls so bezeichnet.
Inhaltsverzeichnis
Definition und weitere Darstellungen
Die dirichletsche η-Funktion wird üblicherweise definiert als
Eine Integraldarstellung enthält die Gammafunktion Γ(s) und lautet
Ihre Funktionalgleichung ist
Eine Reihendarstellung ist gegeben durch
Werte
Es gilt
Für natürliche k gilt mit den Bernoulli-Zahlen Bk
Die Werte für gerade Argumente
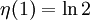 (die alternierende harmonische Reihe)
(die alternierende harmonische Reihe)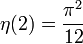
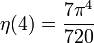
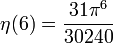
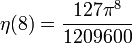
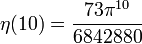
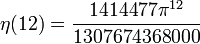
ergeben sich aus der allgemeinen Formel
Die ersten Werte für ungerade Argumente sind
Weiteres
Die Verwandschaften von η zu der dirichletschen λ-Funktion[1] und der riemannschen ζ-Funktion werden durch folgende Formel zum Ausdruck gebracht[2]:
bzw.
Die dirichletsche eta-Funktion ist ein Spezialfall des Polylogarithmus, denn es gilt:
Die Ableitung ist gegeben durch
Außerdem gilt
Literatur
- Eric W. Weisstein: Dirichlet Eta Function auf MathWorld (englisch)
- Milton Abramowitz, Irene Stegun: Handbook of Mathematical Functions, New York: Dover, 1972.
- Konrad Knopp [1922]: Theory and Application of Infinite Series. Dover 1990, ISBN 0-486-66165-2
Einzelnachweise
- ↑ Eric W. Weisstein: Dirichlet Lambda Function auf MathWorld (englisch)
- ↑ J. Spanier, K.B.Oldham: The Zeta Numbers and Related Functions. In: An Atlas of Functions. Washington, DC: Hemisphere, S. 25-33, 1987.
Wikimedia Foundation.

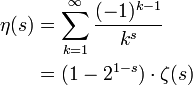
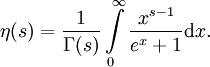
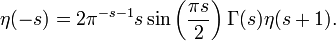
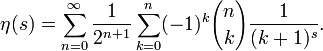
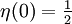
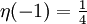
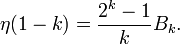
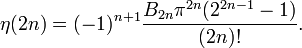
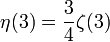
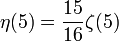
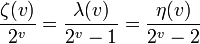
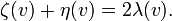
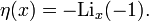
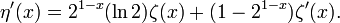
![\int\limits_0^1\int\limits_0^1 \frac{[-\ln(x,y)]^s}{1+xy}\;\mathrm dx\,\mathrm dy=\Gamma(s+2)\eta(s+2).](/pictures/dewiki/102/fb7ce978837aae91df2c35166730c23e.png)