Dirichlet'sche η-Funktion
- Dirichlet'sche η-Funktion
-
In der Zahlentheorie ist die dirichletsche η-Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805−1859) benannt ist. Sie ist verwandt mit der riemannschen ζ-Funktion.
Sie wird mit dem kleinen griechischen Buchstaben eta (η) notiert; die dedekindsche η-Funktion, eine Modulform, wird aber ebenfalls so bezeichnet.
Definition und weitere Darstellungen
Die dirichletsche η-Funktion wird üblicherweise definiert als
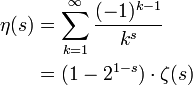
Eine Integraldarstellung enthält die Gammafunktion Γ(s) und lautet
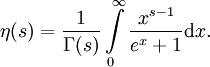
Ihre Funktionalgleichung ist
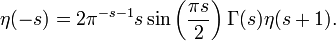
Eine Reihendarstellung ist gegeben durch
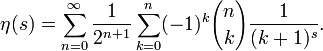
Werte
Es gilt
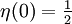
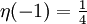
Für natürliche k gilt mit den Bernoulli-Zahlen Bk
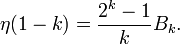
Die Werte für gerade Argumente
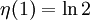 (die alternierende harmonische Reihe)
(die alternierende harmonische Reihe)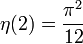
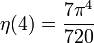
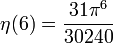
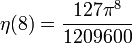
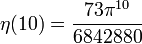
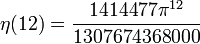
ergeben sich aus der allgemeinen Formel
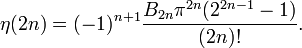
Die ersten Werte für ungerade Argumente sind
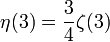
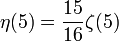
Weiteres
Die Verwandschaften von η zu der dirichletschen λ-Funktion[1] und der riemannschen ζ-Funktion werden durch folgende Formel zum Ausdruck gebracht[2]:
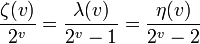
bzw.
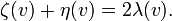
Die dirichletsche eta-Funktion ist ein Spezialfall des Polylogarithmus, denn es gilt:
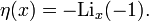
Die Ableitung ist gegeben durch
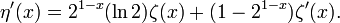
Außerdem gilt
![\int\limits_0^1\int\limits_0^1 \frac{[-\ln(x,y)]^s}{1+xy}\;\mathrm dx\,\mathrm dy=\Gamma(s+2)\eta(s+2).](/pictures/dewiki/102/fb7ce978837aae91df2c35166730c23e.png)
Literatur
Einzelnachweise
- ↑ Eric W. Weisstein: Dirichlet Lambda Function auf MathWorld (englisch)
- ↑ J. Spanier, K.B.Oldham: The Zeta Numbers and Related Functions. In: An Atlas of Functions. Washington, DC: Hemisphere, S. 25-33, 1987.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
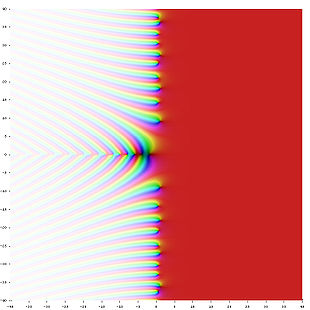
Dirichlet'sche Eta-Funktion — Die dirichletsche η Funktion in der komplexen Zahlenebene. In der Zahlentheorie ist die dirichletsche η Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805−1859) benannt ist. Sie ist verwandt mit der … Deutsch Wikipedia
L-Funktion — Die Theorie der L Funktionen ist ein aktuelles Gebiet der analytischen Zahlentheorie, in welchem Verallgemeinerungen der Riemannsche ζ Funktion und der Dirichletschen L Reihen untersucht werden. Dabei werden ihre allgemeinen Eigenschaften mit… … Deutsch Wikipedia
Gauß'sche Glockenkurve — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… … Deutsch Wikipedia
Gauß-Funktion — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… … Deutsch Wikipedia
Gaußsche Funktion — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… … Deutsch Wikipedia
Maxwell'sche Geschwindigkeitsverteilung — Maxwell Boltzmann Verteilung Parameter Definitionsbereich Wahrscheinlichkeitsdichte … Deutsch Wikipedia
Student'sche t-Verteilung — Dichten von t verteilten Zufallsgrößen Die Studentsche t Verteilung (auch Student t Verteilung) ist eine Wahrscheinlichkeitsverteilung, die 1908 von William Sealey Gosset entwickelt wurde. Er hatte festgestellt, dass der standardisierte… … Deutsch Wikipedia
Georg Friedrich Bernhard Riemann — Bernhard Riemann Georg Friedrich Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore) war ein deutscher Mathem … Deutsch Wikipedia
Bernhard Riemann — 1863 Georg Friedrich Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore) war ein deutscher Mathematiker, der … Deutsch Wikipedia
Gauss-Verteilung — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… … Deutsch Wikipedia
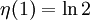 (die alternierende harmonische Reihe)
(die alternierende harmonische Reihe)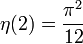
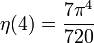
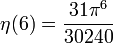
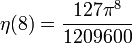
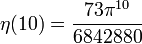
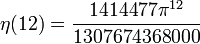

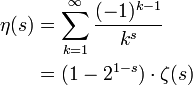
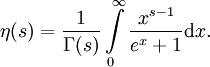
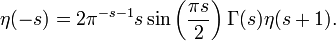
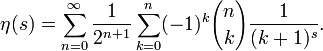
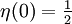
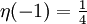
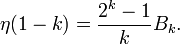
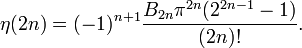
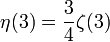
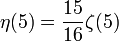
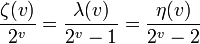
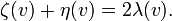
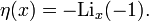
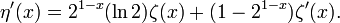
![\int\limits_0^1\int\limits_0^1 \frac{[-\ln(x,y)]^s}{1+xy}\;\mathrm dx\,\mathrm dy=\Gamma(s+2)\eta(s+2).](/pictures/dewiki/102/fb7ce978837aae91df2c35166730c23e.png)