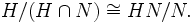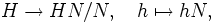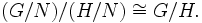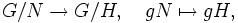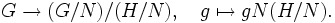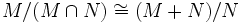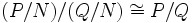Dritter Isomorphiesatz

Die Isomorphiesätze sind zwei mathematische Sätze, die Aussagen über Gruppen machen. Sie lassen sich auch auf komplexere algebraische Strukturen übertragen und sind somit ein wichtiges Resultat der universellen Algebra. Die Isomorphiesätze sind eine direkte Folgerung aus dem Homomorphiesatz der entsprechenden algebraischen Struktur.

Manchmal wird der Homomorphiesatz als erster Isomorphiesatz bezeichnet. Die unten angegebenen Sätze heißen dann dementsprechend zweiter bzw. dritter Isomorphiesatz.

Gruppentheorie

Erster Isomorphiesatz

Es seien G eine Gruppe, N ein Normalteiler in G und H eine Untergruppe von G. Dann ist auch das Produkt 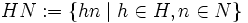$HN:=\{hn\mid h\in H, n\in N\}$ eine Untergruppe von G, N ist ein Normalteiler in HN und die Gruppe 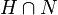$H\cap N$ ist ein Normalteiler in H. Es gilt:

$H/(H\cap N)\cong HN/N.$

Dabei bezeichnet 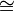$\cong$ die Isomorphie von Gruppen.

Der Isomorphismus, der dabei üblicherweise gemeint ist, wird als kanonischer Isomorphismus bezeichnet. Er wird gemäß dem Homomorphiesatz von der surjektiven Abbildung

$H\to HN/N,\quad h\mapsto hN,$

induziert.

Anschaulich ausgedrückt besagt der 1. Isomorphiesatz, dass man mit N "erweitern" darf.

Zweiter Isomorphiesatz

Es seien G eine Gruppe, H ein Normalteiler in G und N eine Untergruppe von H, die Normalteiler in G ist. Dann gilt:

• $(G/N)/(H/N)\cong G/H.$

In diesem Fall kann man kanonische Isomorphismen in beide Richtungen angeben, einerseits induziert durch

$G/N\to G/H,\quad gN\mapsto gH,$

andererseits durch

$G\to(G/N)/(H/N),\quad g\mapsto gN(H/N).$

Anschaulich ausgedrückt besagt der 2. Isomorphiesatz, dass man N "kürzen" darf.

Vektorräume, abelsche Gruppen oder Objekte einer beliebigen abelschen Kategorie

Es seien $M,N\subseteq Q\subseteq P$

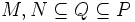
• Vektorräume über einem Körper
• oder abelsche Gruppen
• oder allgemeiner Moduln über einem Ring
• oder ganz allgemein Objekte einer abelschen Kategorie.

Dann gilt:

• $M/(M\cap N)\cong (M+N)/N$
• $(P/N)/(Q/N)\cong P/Q$

Auch hier steht das Symbol 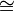$\cong$ für die Isomorphie der entsprechenden algebraischen Strukturen bzw. Objekte in der jeweiligen Kategorie.

Die kanonischen Isomorphismen sind eindeutig dadurch bestimmt, dass sie mit den beiden kanonischen Pfeilen von M bzw. P kompatibel sind.

Eine weitreichende Verallgemeinerung der Isomorphiesätze liefert das Schlangenlemma.

Weblinks

matheplanet.com: Gruppenzwang IV - Ausführliche Erklärungen und Beweise der Isomorphiesätze