- Affine Chiffrierung
-
Die affine Chiffre ist ein Verschlüsselungsverfahren. Bei diesem Verfahren wird der Klartext Buchstabe für Buchstabe nach einer bestimmten mathematischen Formel verschlüsselt. Die affine Chiffre lässt sich zwar ohne größeren Aufwand berechnen, dafür ist sie allerdings nicht besonders sicher. Einerseits gibt es nur eine begrenzte Anzahl geheimer Schlüssel, sodass diese alle durchprobiert werden können. Andererseits kann der Geheimtext entschlüsselt werden, sobald die Verschlüsselung von nur zwei Zeichen bekannt ist.
Inhaltsverzeichnis
Verfahren
Lateinisches Alphabet
Dieser Abschnitt zeigt die Verwendung der affinen Chiffre für das lateinische Alphabet mit seinen 26 Buchstaben.
Geheimer Schlüssel
Sender und Empfänger müssen sich vor Verwendung der affinen Chiffre auf einen geheimen Schlüssel verständigen. Dieser Schlüssel ist ein Zahlenpaar (a,b), wobei a eine der Zahlen 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23 oder 25 und b eine beliebige Zahl von 0 bis 25 ist. Für a gilt dabei a < b und ggT(a,b) = 1 und b ist die Anzahl der Buchstaben des Alphabets.
Als Beispiel wird im Folgenden die Ver- und Entschlüsselung mit dem Schlüssel (7,15) betrachtet.
Verschlüsselung
Zur Verschlüsselung werden die Buchstaben des Alphabets fortlaufend durchnummeriert: A=0, B=1, …. Man verschlüsselt jeden Buchstaben einzeln, indem man seinen Zahlenwert x mit a multipliziert und anschließend b addiert. Das Ergebnis teilt man dann durch 26.
Der bei dieser Division auftretende Rest ist die Nummer des verschlüsselten Buchstabens.
Will man beispielsweise den Buchstaben S, dem die Zahl 18 zugeordnet ist, mit dem Schlüssel (7,15) verschlüsseln, so berechnet man
Das S wird dann durch das L (dem Buchstaben mit der Nummer 11) ersetzt.
Entschlüsselung
Zu jeder Zahl a des Schlüssels gibt es eine zweite Zahl a − 1, die der folgenden Tabelle entnommen werden kann.
-
a: 1 3 5 7 9 11 15 17 19 21 23 25 a − 1: 1 9 21 15 3 19 7 23 11 5 17 25
Mit den Zahlen a − 1 und b des Schlüssels lässt sich der Geheimtext wieder entschlüsseln. Man nimmt dazu den Zahlenwert y des Geheimtextbuchstabens, berechnet
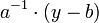 und teilt das Ergebnis wieder durch 26.
und teilt das Ergebnis wieder durch 26.Auch bei dieser Division tritt ein Rest auf, der die Nummer des Buchstabens vor der Verschlüsselung angibt.
Um beispielsweise den Buchstaben L wieder zu entschlüsseln, schlägt man in der Tabelle a − 1 = 15 nach und berechnet
Der Rest 18 zeigt, dass der ursprünglich Buchstabe ein S war. (Anstatt durch 26 zu teilen kann man bei negativen Zahlen auch sooft 26 addieren, bis man eine positive Zahl erhält. Diese Zahl ist mit dem Rest der Division identisch.)
Beliebiges Alphabet
Anstatt des lateinischen lässt sich jedes andere Alphabet verwenden. Auch hier werden die einzelnen Buchstaben beginnend mit der Null durchnummeriert. Im Weiteren bezeichnet m die Anzahl der Zeichen des Alphabets.
Der geheime Schlüssel ist ein Zahlenpaar (a,b), wobei sowohl a als auch b Zahlen von 0 bis m − 1 sind. Die Zahl a muss zusätzlich noch teilerfremd zu m sein.
Zur Verschlüsselung verwendet man den Modulo-Operator, der dem Rest bei der Division entspricht. Ist x das zu verschlüsselnde Zeichen, dann berechnet sich das zugehörige Zeichen y des Geheimtexts nach der Formel
Zur Entschlüsselung berechnet man das multiplikativ inverse Element a − 1 mit Hilfe des erweiterten euklidischen Algorithmus. Anschließend erhält man das ursprünglich Zeichen aus dem Zeichen des Geheimtexts nach der Formel
Verschiebechiffre
Wenn a = 1 ist, wird die Affine Chiffre als Verschiebechiffre bezeichnet. Bei einer Verschiebung um b = 3 handelt es sich um die Caesar-Chiffre.
Sicherheit
Die affine Chiffre ist ein sehr schwaches Verschlüsselungsverfahren. Es gibt zwei Methoden um sie zu brechen. Am einfachsten ist es, alle möglichen geheimen Schlüssel auszuprobieren. Eine schnellere Methode kann angewandt werden, wenn zu zwei Buchstaben des Geheimtextes die jeweiligen Klartextbuchstaben bekannt sind. Dann lässt sich der geheime Schlüssel in wenigen Schritten berechnen. Zu den beiden notwendigen Buchstabenpaare gelangt man beispielsweise durch eine Häufigkeitsanalyse.
Literatur
- Johannes Buchmann: Einführung in die Kryptographie. 2. Auflage, Springer, 2001, ISBN 3-540-41283-2, S. 73–74
Wikimedia Foundation.

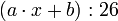
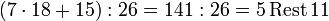
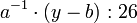
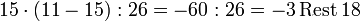
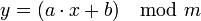
![x = \left[ a^{-1} \cdot (y - b) \right] \mod m](/pictures/dewiki/50/2bfd8aa1a0f9a4aef0ebdf5fe9c5b1ad.png)