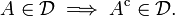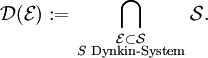- Dynkinsystem
-
Ein Dynkin-System
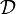 auf einer nichtleeren Grundmenge Ω bezeichnet in der Maßtheorie, einem Teilgebiet der Mathematik, ein System von Teilmengen von Ω (ähnlich der σ-Algebra). Es ist benannt nach dem russischen Mathematiker Eugene Dynkin.
auf einer nichtleeren Grundmenge Ω bezeichnet in der Maßtheorie, einem Teilgebiet der Mathematik, ein System von Teilmengen von Ω (ähnlich der σ-Algebra). Es ist benannt nach dem russischen Mathematiker Eugene Dynkin.Inhaltsverzeichnis
Definition
Eine Teilmenge
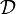 der Potenzmenge
der Potenzmenge 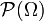 von Ω heißt Dynkin-System, falls sie die folgenden Eigenschaften besitzt:
von Ω heißt Dynkin-System, falls sie die folgenden Eigenschaften besitzt:- Die ganze Grundmenge ist im System enthalten:
- Das System ist abgeschlossen bezüglich Komplementbildung:
- Das System ist abgeschlossen bezüglich abzählbarer, disjunkter Vereinigungen:
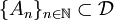 disjunkt
disjunkt 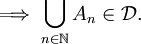
Aus
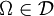 und der Abgeschlossenheit bezüglich Komplementbildung folgt somit insbesondere, dass auch die leere Menge
und der Abgeschlossenheit bezüglich Komplementbildung folgt somit insbesondere, dass auch die leere Menge 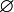 in
in 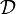 ist.
ist.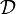 -Operator
-OperatorDas von einer Menge
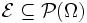 erzeugte Dynkin-System ist
erzeugte Dynkin-System ist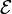 wird als Erzeuger von
wird als Erzeuger von 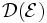 bezeichnet.
bezeichnet.
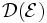 ist das kleinste Dynkin-System, welches
ist das kleinste Dynkin-System, welches 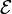 enthält.
enthält.Zusammenhang mit σ-Algebra
- Jede σ-Algebra ist ein Dynkin-System.
- Ein Dynkin-System
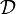 ist genau dann eine σ-Algebra, wenn es durchschnittsstabil ist.
ist genau dann eine σ-Algebra, wenn es durchschnittsstabil ist. - Für jede durchschnittsstabile Teilmenge
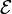 von
von 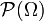 gilt, dass das erzeugte Dynkin-System mit der erzeugten σ-Algebra übereinstimmt:
gilt, dass das erzeugte Dynkin-System mit der erzeugten σ-Algebra übereinstimmt: 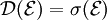 (siehe σ-Operator).
(siehe σ-Operator).
Das Dynkin-System-Argument
Mit Dynkin-Systemen lassen sich in vielen Fällen Aussagen über σ-Algebren relativ einfach beweisen. Sei α eine Aussage, die für Mengen
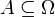 entweder zutrifft oder nicht. Weiter sei Σ eine σ-Algebra mit einem durchschnittsstabilen Erzeuger
entweder zutrifft oder nicht. Weiter sei Σ eine σ-Algebra mit einem durchschnittsstabilen Erzeuger 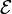 , für dessen Elemente man α zeigen kann. Betrachte nun das Mengensystem
, für dessen Elemente man α zeigen kann. Betrachte nun das Mengensystem 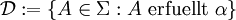 und zeige, dass es ein Dynkin-System ist. Dann folgt wegen der Durchschnittsstabilität von
und zeige, dass es ein Dynkin-System ist. Dann folgt wegen der Durchschnittsstabilität von 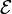 einerseits
einerseits 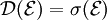 , andererseits gilt aber auch
, andererseits gilt aber auch 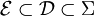 und damit wegen
und damit wegen 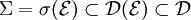 schon
schon 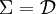 .
.Die definierenden Eigenschaften eines Dynkin-Systems sind oft einfacher nachzuweisen, weil bei der Abgeschlossenheit gegenüber abzählbarer Vereinigung nur Folgen von paarweise disjunkten Einzelmengen betrachtet werden müssen, während bei σ-Algebren diese Zusatzeigenschaft nicht zur Verfügung steht.
Literatur
- Heinz Bauer: Maß- und Integrationstheorie. Walter de Gruyter, Berlin - New York 1992, ISBN 3-11-013626-0
Wikimedia Foundation.