Mengensystem

Ein Mengensystem ist in der Mathematik eine Menge, deren Elemente allesamt Teilmengen einer gemeinsamen Grundmenge sind.

Im Kontext der Graphentheorie wird ein Mengensystem als Hypergraph bezeichnet.

Formale Definition

Ist eine Grundmenge X gegeben, so heißt jede Teilmenge S der Potenzmenge $\mathcal P(X) = \{A \mid A \subseteq X\}$ ein Mengensystem über X. Anders ausgedrückt: S ist eine Menge von Mengen und jedes Element von S ist eine Teilmenge von X.

Stabilität

Ein Mengensystem S heißt abgeschlossen oder stabil bezüglich einer Mengenoperation (Durchschnitt, Vereinigung, Komplement, etc.), wenn die Anwendung der Operation auf Elemente von S wieder ein Element von S liefert. Zum Beispiel ist S durchschnittsstabil, wenn gilt, dass der Durchschnitt zweier Mengen aus S wieder in S liegt. In Formeln:

$A, B \in S \Rightarrow A \cap B \in S.$

Beispiele

Die folgenden mathematischen Objekte sind Mengensysteme mit zusätzlichen Eigenschaften. Bei der Formulierung dieser Eigenschaften spielt oft die Stabilität bezüglich bestimmter Mengenoperationen eine Rolle.

Dynkin-System Fréchet-Filter Hüllensystem Kernsystem Matroid Mengenalgebra Mengenfilter Mengenhalbring

Mengenring Partition Potenzmenge σ-Algebra Topologischer Raum Ungerichteter Graph Zermelosystem

Ein Hypergraph mit 7 Knoten und 4 Hyperkanten

Ein ungerichteter Graph mit 6 Knoten und 7 Kanten

Hypergraphen

Im Kontext der Graphentheorie wird ein Mengensystem auch als Hypergraph bezeichnet. Die Elemente der Grundmenge heißen dann Knoten und die Elemente des Mengensystems heißen Hyperkanten. Man kann sich eine Hyperkante als Verallgemeinerung einer Kante in einem gewöhnlichen Graphen vorstellen, die eben nicht zwei, sondern mehrere Knoten gleichzeitig miteinander „verbindet“. Im nebenstehenden Beispiel gilt:

Menge der Knoten = {v₁,v₂,v₃,v₄,v₅,v₆,v₇}

Menge der Hyperkanten = {e₁,e₂,e₃,e₄}, wobei

Hyperkante e₁ = {v₁,v₂,v₃}

Hyperkante e₂ = {v₂,v₃}

Hyperkante e₃ = {v₃,v₅,v₆}

Hyperkante e₄ = {v₄}

In vielen Anwendungsfällen von Hypergraphen wird die Knotenmenge als endlich festgelegt und die leere Hyperkante ausgeschlossen.

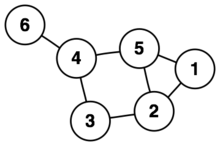
Verbindet jede Hyperkante genau 2 Knoten, liegt ein ungerichteter Graph vor (genauer: ein ungerichteter Graph ohne Mehrfachkanten und ohne Schleifen). Das Mengensystem besteht dann also nur aus 2-elementigen Teilmengen der Grundmenge. Im nebenstehenden Beispiel gilt:

Grundmenge = {1,2,3,4,5,6}

Mengensystem = {{1,2},{1,5},{2,3},{2,5},{3,4},{4,5},{4,6}}

Axiomatische Mengenlehre

In der Zermelo-Fraenkel-Mengenlehre gibt es nur einen Typ von Objekten, nämlich Mengen. Damit sind alle Elemente einer Menge selbst wieder Mengen, und die Begriffe Menge und Mengensystem stimmen überein.

Beispiel: Jede natürliche Zahl wird in diesem Zusammenhang mit der Menge ihrer Vorgänger identifiziert. Dies ergibt den folgenden Aufbau:

$0 = \varnothing$ (die leere Menge)

$1 = \{0\} = \{\varnothing\}$

$2 = \{0, 1\} = \{ \varnothing, \{ \varnothing\} \}$

$3 = \{0, 1, 2\} = \{ \varnothing, \{ \varnothing\}, \{ \varnothing, \{ \varnothing\} \} \}$

$4 = \{0, 1, 2, 3\}\ = \ldots$

    $\vdots$

Literatur

• Oliver Deiser: Einführung in die Mengenlehre, Springer, 2004, ISBN 978-3540204015