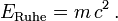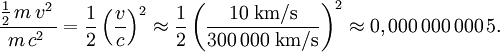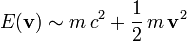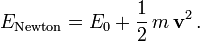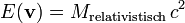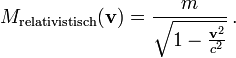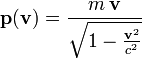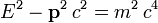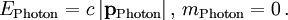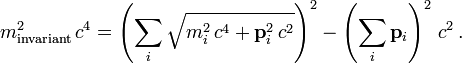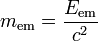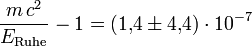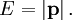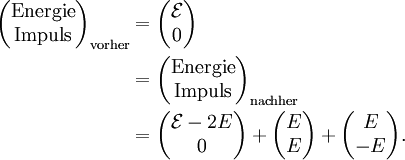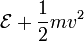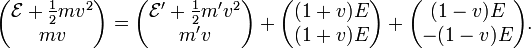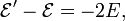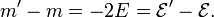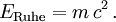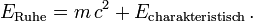E=mc²

„Relativitätstheorie“, sechste und letzte Skulptur beim Berliner Walk of Ideas zur FIFA-Fußball-Weltmeisterschaft in Deutschland 2006

Die Äquivalenz von Masse und Energie ist die Erkenntnis der relativistischen Physik, dass die Energie E_Ruhe jedes ruhenden Teilchens und seine Masse m sich gegenseitig festlegen; die Ruheenergie ist doppelt so groß wie in der Newtonschen Mechanik die kinetische Energie des Teilchens wäre, wenn es sich mit Lichtgeschwindigkeit c bewegte:

$E_{\text{Ruhe}}=m\, c^2\,.$

Da die Lichtgeschwindigkeit um ein Vielfaches größer ist als Geschwindigkeiten in unserer alltäglichen Umgebung, übersteigt die an der Masse ablesbare Ruheenergie die kinetische Energie in alltäglichen Situationen um viele Größenordnungen. Zwar lässt die in Wärme umgewandelte kinetische Energie eine Raumkapsel bei der Rückkehr verglühen, wenn sie nicht abgeschirmt wird, dabei ist die kinetische Energie nur ein winziger Bruchteil, ein Milliardstel, der Ruheenergie,

$\frac{\frac{1}{2}\,m\, v^2\,}{m\, c^2\,}=\frac{1}{2}\left(\frac{v}{c}\right)^2\approx \frac{1}{2}\left(\frac{10\;\text{km/s}}{300\,000\;\text{km/s}}\right)^2 \approx 0,000\,000\,000\,5.$

Wenn nicht Erhaltungsgrößen wie elektrische Ladung oder Baryonenzahl es verhindern, können Teilchen in andere Teilchen mit geringeren Massen übergehen und die dabei freiwerdende Ruheenergie in andere Energieformen wie Strahlung und kinetische Energie anderer Teilchen umgewandelt werden. Beispielsweise wird bei der Kernspaltung Ruheenergie freigesetzt.

Erläuterung

Bei einem ruhenden Teilchen sind Masse und Energie äquivalent, das heißt, bis auf einen konstanten Faktor gleich. Aber allgemeiner, bei bewegten Teilchen, bezeichnen Masse und Energie Größen, die sich in mehr als in einem konstanten Faktor unterscheiden.

Wenn die Geschwindigkeit gegen die Lichtgeschwindigkeit geht, wächst die Energie über alle Grenzen.

Energie

• Die Energie 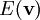$E(\mathbf{v})$ eines Teilchens der Masse 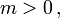$m>0\,,$ das sich mit Geschwindigkeit 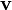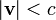$\mathbf{v}$, $|\mathbf{v}|<c$, bewegt, ist eine Funktion der Geschwindigkeit

$\ E(\mathbf{v})= \frac{m\,c^2}{\sqrt{1-\frac{\mathbf{v}^2}{c^2}}}\$

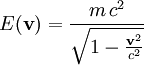
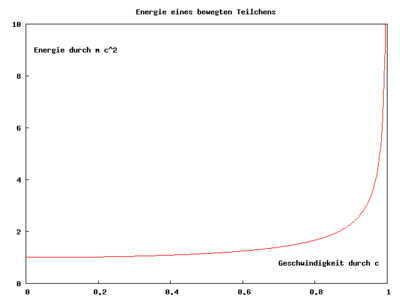
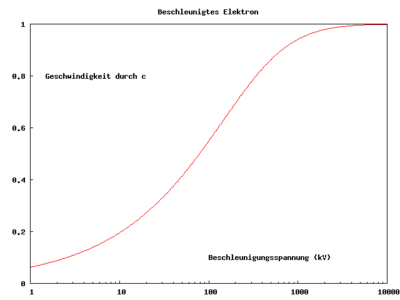
und bezeichnet eine Erhaltungsgröße. In Stößen und anderen Teilchenreaktionen stimmt die Summe der anfänglichen Energien mit der Summe der späteren Energien überein. Weil unendlich viel Energie erforderlich wäre, Lichtgeschwindigkeit zu erreichen, können Teilchen mit positiver Masse die Lichtgeschwindigkeit nicht erreichen oder überschreiten.

Ruhemasse

• Die hier auftretende Masse m hat einen festen, für das Teilchen charakteristischen, positiven Wert. Sie wurde historisch Ruhemasse genannt. Die Energie und der Impuls eines Teilchens hängen stets durch die Energie-Impuls-Beziehung (siehe unten) mit der Masse zusammen. Die Ruhemasse eines Teilchens ist diejenige Masse, die ein relativ zu diesem ruhender Beobachter misst.

Klassische Näherung

Zerfällt ein Atomkern, so ist seine Masse größer als die Summe der Massen der Tochterteilchen. Seine Energie hingegen stimmt mit der Summe der Energien der Zerfallsprodukte überein.

Auch mit wachsender Energie bleibt das Elektron langsamer als Licht.

Für kleine Geschwindigkeiten, 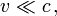$v \ll c\,,$ wie sie alltäglich auftreten, ist die Energie näherungsweise

$E(\mathbf{v})\sim m\,c^2 + \frac{1}{2}\,m \,\mathbf{v}^2$

so wie in Newtons Mechanik,

$E_{\text{Newton}}= E_0 + \frac{1}{2}\,m \,\mathbf{v}^2\,.$

Allerdings hat dort die Energie E₀ eines ruhenden Teilchens keinen Zusammenhang zu seiner Masse. Sie könnte irgendeinen, für jedes Teilchen charakteristischen Wert haben. Daher sind in Newtons Mechanik Zerfälle von schweren Teilchen in leichte genauso denkbar wie umgekehrt.

Bei höheren Geschwindigkeiten zeigen Messungen, dass die Energie E_Newton keine Erhaltungsgröße ist: Nur die Summe der relativistischen Energien aller einlaufenden Teilchen stimmt bei Stößen und anderen Teilchenreaktionen mit der Summe der relativistischen Energien der auslaufenden Teilchen überein.

Relativistische Masse

Ordnet man der Energie des Teilchens, das sich mit der Geschwindigkeit 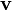$\mathbf v$ bewegt, durch

$E(\mathbf v) =M_{\text{relativistisch}}\, c^2$

rechnerisch eine Masse zu, so hängt diese Masse von der Geschwindigkeit ab. Sie heißt relativistische Masse,

$M_{\text{relativistisch}}(\mathbf v)=\frac{m}{\sqrt{1-\frac{\mathbf{v}^2}{c^2}}}\,.$

Mit ihr schreibt sich der relativistische Impuls wie in Newtons Mechanik als Masse mal Geschwindigkeit.

In manchen Darstellungen der relativistischen Physik wird die relativistische Masse kurz Masse genannt. Dies verleitet zur Fehlvorstellung, man könne die relativistische Masse so wie eine ruhende Masse mit einer Waage im Gravitationsfeld messen oder so wie eine langsam bewegte Masse durch ihre Trägheit aus Newtons Bewegungsgleichungen ablesen. Falsch ist auch die Unterstellung, die Gravitationskraft, mit der ein bewegtes Teilchen ein anderes anzieht, sei proportional zur relativistischen Masse, ebenso falsch die Ansicht, bei hoher Geschwindigkeit würden Teilchen wegen ihrer großen relativistischen Massen Schwarze Löcher.

Der Begriff der relativistischen Masse wird in der modernen Physik gemieden, um ohne Wortzusätze von verschiedenen Begriffen mit verschiedenen Wörtern zu reden. Auch Einstein erschien es nicht gut, von M_{relativistisch} als Masse zu sprechen, man bezeichne mit diesem Wort besser die Ruhemasse.^[1]

Das Wort Masse bezeichnet wie in Newtons Physik eine für das Teilchen charakteristische Größe, die nicht von der Geschwindigkeit und dem Beobachter abhängt. Die Energie ist wie in Newtons Physik geschwindigkeitsabhängig und für verschieden bewegte Beobachter verschieden. Die Energie hat bei allen Vorgängen den unveränderten Wert, den sie zu Beginn hatte. Sie ist eine additive Erhaltungsgröße. Die Masse hingegen kann bei Teilchenzerfällen abnehmen.

Massenschale

Da der Impuls eines Teilchens der Masse m, das sich mit Geschwindigkeit 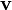$\mathbf{v}$ bewegt, in relativistischer Physik

$\mathbf{p}(\mathbf{v})=\frac{m\,\mathbf{v}}{\sqrt{1-\frac{\mathbf{v}^2}{c^2}}}$

beträgt (Herleitung siehe Viererimpuls), hängen die Energie und der Impuls mit der Masse durch die Energie-Impuls-Beziehung

$E^2-\mathbf{p}^2\,c^2 = m^2\,c^4$

zusammen. Im vierdimensionalen Raum aller denkbaren Energie- und Impulswerte liegen gemäß dieser Gleichung die physikalisch möglichen Energien eines Teilchens der Masse m auf einer dreidimensionalen Fläche, der sogenannten Massenschale. Sie ist ein Hyperboloid (y² − x² = 1 beschreibt eine Hyperbel in der x-y-Ebene).

Die Energie-Impuls-Beziehung gilt auch für Photonen. Sie sind masselos und bewegen sich stets mit Lichtgeschwindigkeit. Die Energie eines Photons ist bis auf einen Faktor c der Betrag seines Impulses, seine Masse verschwindet,

$E_{\text{Photon}}= c\,|\mathbf{p}_{\text{Photon}}|\,,\,m_{\text{Photon}}=0\,.$

Invariante Masse

Addiert man bei Teilchenstößen und Teilchenumwandlungen die Energien und Impulse der Teilchen, die anfänglich vorhanden sind, dann definieren die Energie und der Impuls durch die Energie-Impuls-Beziehung eine Masse, die invariante Masse 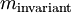$m_{\text{invariant}}\,$ der anfänglichen Teilchen

$m_{\text{invariant}}^2\,c^4 = \left(\sum_i\sqrt{m_i^2\,c^4+\mathbf p_i^2\,c^2}\right)^2 -\left(\sum_i \mathbf p_i\right)^2\,c^2\,.$

Sie ist eine Funktion der erhaltenen Energie und des erhaltenen Impulses und demnach selbst eine Erhaltungsgröße. Sie stimmt also mit der analog berechneten invarianten Masse der Teilchen überein, die später nach einer Wechselwirkung auslaufen.

Die invariante Masse ist jedoch keine additive Erhaltungsgröße: Die invariante Masse mehrerer Teilchen ist größer als die Summe der einzelnen invarianten Massen. Mit c² multipliziert hat die invariante Masse die Bedeutung der Energie der einlaufenden Teilchen in ihrem Schwerpunktsystem. Sie schränkt denkbare Teilchenreaktionen ein: Es können nur solche Teilchen entstehen, deren summierte Massen kleiner als die invariante Masse der Ausgangsteilchen sind. Die Werte der invarianten Masse von Zwei- oder Mehrteilchensystemen sind, anders als die diskreten Massen elementarer Teilchen, kontinuierlich. Findet man bei Zusammenfassung der Energien und Impulse einer Untergruppe von auslaufenden Teilchen immer wieder denselben Wert der invarianten Masse, so weist dies darauf hin, dass es sich um die Zerfallsprodukte eines Teilchens dieser Masse handelt.

Geschichte

Der Zusammenhang zwischen Masse, Energie, und Lichtgeschwindigkeit wurde bereits ab 1880 von unterschiedlichen Autoren im Rahmen von Maxwells Elektrodynamik bedacht. Joseph Thomson (1881), Oliver Heaviside (1889), George Searle (1897), Wilhelm Wien (1900), Max Abraham (1902), und Hendrik Lorentz (1904) erschlossen, dass die elektromagnetische Energie dem Körper eine „elektromagnetische Masse“ hinzufügt gemäß der Formel

$m_{\text{em}} = \frac{4}{3} \frac{E_{\text{em}}}{c^2}$.

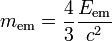Zu derselben Formel gelangte Friedrich Hasenöhrl (1904) durch Betrachtung der elektromagnetischen Hohlraumstrahlung eines Körpers. Henri Poincaré (1900) hingegen folgerte aus Betrachtungen zum Reaktionsprinzip, dass elektromagnetische Energie einer „fiktiven“ Masse von

$m_{\text{em}} = \frac{E_{\text{em}}}{c^2}$

entspricht.^[2][3] Die elektromagnetische Masse wurde häufig auch als „scheinbare“ Masse bezeichnet, da man diese vorerst von der „wahren“, mechanischen Masse Newtons unterschied. Aber es wurden von Wien und Abraham schon Versuche unternommen, der gesamten Masse einen elektromagnetischen Ursprung zuzuschreiben.

Aber erst Albert Einstein (1905) war es dann, der die gesamte Ruheenergie durch

$E_{\text{Ruhe}} = m\,c^2$

mit der gesamten Masse in eine Beziehung setzte, die in eine umfassende Theorie, die Spezielle Relativitätstheorie, eingebettet war. Dabei ergab sich, dass alle vorhergehenden Spekulationen über die elektromagnetische Natur der Masse in eine falsche Richtung wiesen, denn in der Speziellen Relativitätstheorie gilt ausnahmslos die Äquivalenz von Masse und Ruheenergie, unabhängig davon, ob die Masse elektromagnetischen Ursprungs ist oder nicht.

Diese Äquivalenz wurde ursprünglich auch „Trägheit der Energie“ genannt, da man jeder Form von Energie eine träge Masse 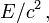$E/c^2\,,$ die relativistische Masse, zuschrieb.^[4] Solch ein Wortgebrauch ist jedoch, wie im Abschnitt relativistische Masse besprochen, irreführend, denn die Trägheit eines schnell bewegten Teilchen hängt von seiner Bewegungsrichtung ab.

Die quantitative Übereinstimmung von Kernmassenunterschieden und Bindungsenergien konnte ab den 1930er Jahren gemessen werden.^[5][6] Heute ist die Gültigkeit der Äquivalenz von Masse und Energie experimentell mit einer Genauigkeit von

$\frac{m\,c^2}{E_{\text{Ruhe}}}-1 = (1{,}4 \pm 4{,}4) \cdot 10^{-7}$

bestätigt.^[7]

Siehe: Lorentzsche Äthertheorie#Masse, Energie und Geschwindigkeit

Siehe: Geschichte der speziellen Relativitätstheorie

E=mc² und die Atombombe

Anders als populärwissenschaftliche Berichte behaupten (Titelbild von Time Magazine Juli 1946) spielte der Zusammenhang von Ruheenergie und Masse bei der Entwicklung der Atombombe Anfang der 1940er Jahre keine besondere Rolle. Bei radioaktiver Strahlung hatten Antoine Becquerel, Marie und Pierre Curie, und Ernest Rutherford ab 1897 beobachtet, dass Kernreaktionen millionenfach energiereicher sind als chemische Reaktionen. Mit Einsteins Gleichung 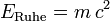$E_{\text{Ruhe}}=m\,c^2$ (1905) konnte man diese Energie an den unterschiedlichen Kernmassen ablesen.

Allerdings besagt die Gleichung nicht, wie man die Spaltung schwerer Atomkerne in Gang setzt. Entscheidend war die Beobachtung der induzierten Kernspaltung durch Otto Hahn und Fritz Straßmann und dass die dabei freiwerdenden Neutronen eine Kettenreaktion in angereichertem Uran auslösen können.^[8]

Albert Einstein beeinflusste die Entwicklung der Atombombe weniger durch seine physikalischen Erkenntnisse, sondern allenfalls politisch, nämlich durch seinen Brief an Präsident Roosevelt, in dem er für die Entwicklung der Atombombe durch die Amerikaner eintrat.

Einsteins Herleitung

Einstein kam 1905 ^[9] durch das folgende Gedankenexperiment auf den Zusammenhang von Masse und Energie. Ein ähnliches Gedankenexperiment hatte Poincaré 1900 bedacht, aber nicht befriedigend klären können. ^[10]

Um die folgenden Überlegungen einfach zu halten, benutzen wir als Längeneinheit die Strecke, die Licht in einer Sekunde zurücklegt, und nennen diese Länge eine Sekunde. In solchen Maßeinheiten ist die Lichtgeschwindigkeit eine Sekunde pro Sekunde, $c=1\,.$

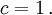
Aus der Elektrodynamik war bekannt, dass ein Lichtpuls nicht nur Energie E besitzt, sondern auch Impuls 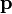$\mathbf p$ in Richtung des Lichtstrahls. In Maßeinheiten mit c = 1 ist der Betrag des Impulses gleich der Energie

$E = |\mathbf p|\,.$

Wenn nun ein ruhender Körper mit Energie 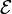$\mathcal{E}$ und der Masse m zwei Photonen mit Energie E in entgegengesetzte Richtung ausstrahlt, so vermindert sich wegen der Erhaltung von Energie und Impuls seine Energie um 2E, er bleibt aber in Ruhe und sein Impuls verschwindet auch nachher, weil die Impulse der Photonen entgegengesetzt gleich sind. Fassen wir die beteiligten Energien und Impulse übersichtlich in Spalten zusammen, so lautet die Energie-Impulsbilanz vor und nach dem Abstrahlen der Photonen

$\begin{align} \begin{pmatrix} \text{Energie}\\ \text{Impuls} \end{pmatrix}_{\text{vorher}} &= \begin{pmatrix} \mathcal E\\ 0 \end{pmatrix}\\ &= \begin{pmatrix} \text{Energie}\\ \text{Impuls} \end{pmatrix}_{\text{nachher}}\\ &= \begin{pmatrix} \mathcal E-2E \\0 \end{pmatrix}+ \begin{pmatrix} E\\ E \end{pmatrix}+ \begin{pmatrix} E\\ -E \end{pmatrix}. \end{align}$

Aus der Sicht eines (in Richtung der Photonen) bewegten Beobachters bewegt sich der Körper vor und nach dem Abstrahlen der Photonen mit einer Geschwindigkeit v. Vor dem Abstrahlen hat er die Energie

$\mathcal E+\frac 12mv^2$

(die Summe von Ruheenergie und kinetischer Energie) und einen Impuls 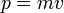$\,p = m v$, zumindest wenn die Geschwindigkeit 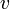$\,v$ so klein gegen die Lichtgeschwindigkeit ist, dass Newtons Mechanik zutrifft.

Das Photon, das der Beobachter mit dem Körper auf sich zukommen sieht, sieht er blauverschoben mit einer um den Dopplerfaktor 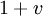$\,1+v$ vergrößerten Energie und entsprechend vergrößertem Impuls.

Das Photon in Gegenrichtung ist für ihn rotverschoben und hat eine um den Dopplerfaktor 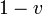$\,1-v$ verminderte Energie und entsprechend verkleinerten Betrag des Impulses. Diese Gleichungen gelten wie Newtons Mechanik für kleine Geschwindigkeiten. Die Energie-Impuls-Bilanz für ein langsam bewegtes Teilchen vor und nach den Aussenden der Photonen lautet also

$\begin{pmatrix} \mathcal E+\frac 12 mv^2\\ mv \end{pmatrix} = \begin{pmatrix} \mathcal E'+\frac 12 m'v^2\\ m'v \end{pmatrix}+ \begin{pmatrix} (1+v)E\\ (1+v)E \end{pmatrix} + \begin{pmatrix} (1-v)E\\ -(1-v)E \end{pmatrix}.$

Dabei bezeichnet m' die Masse und

$\mathcal E'+\frac 12 m'v^2$

die Energie des Körpers nach dem Abstrahlen. Die erste Zeile dieser Gleichung, die Energie-Erhaltung, besagt, wenn wir Terme vernachlässigen, die quadratisch in der Geschwindigkeit sind,

$\mathcal E' -\mathcal E = - 2 E,$

dass sich die Ruheenergie des Körpers beim Abstrahlen um 2E vermindert hat. In der zweiten Zeile besagt Impulserhaltung 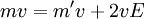$\,mv = m'v + 2vE$, dass sich die Masse ebenso vermindert hat,

$m'-m = -2E = \mathcal E' -\mathcal E.$

Da sich (bis auf die einfachheitshalber weggelassenen Faktoren c) die Masse so wie die Ruheenergie ändert, ist sie die Ruheenergie

$\,E_{\text{Ruhe}}= m\,c^2\,.$

So schön Einsteins Gedankenexperiment ist, die Folgerung ist nicht zwingend: Kein stabiles Teilchen, kein Elektron, Proton oder Neutron, kann in Ruhe Photonen abstrahlen. Das ist physikalisch nur möglich, wenn man auf das Teilchen die dazu erforderliche Energie und den erforderlichen Impuls überträgt.

Es gibt aber auch einen logischen Einwand. Einsteins Überlegung zeigt nur, dass die Differenzen von Masse und Energie bis auf den Faktor c² gleich sind. Das wäre auch der Fall, wenn zur Ruheenergie eine für jedes Teilchen charakteristische, von der Masse unabhängige Energie beitrüge,

$\,E_{\text{Ruhe}}= m\,c^2 + E_{\text{charakteristisch}}\,.$

Dass der Zusatzterm verschwindet, und wie die Energie und der Impuls von der Geschwindigkeit abhängen, ergibt sich aus ihrem Transformationsverhalten (siehe Viererimpuls).

Siehe auch

• Masse (Physik)
• Massendefekt
• Photonenwaage
• Viererimpuls
• Vierervektor

Weblinks

• E=mc² – Eine Formel und ihre Geschichte Populäre Erklärung der Formel mit Grafiken
• Cornelius C. Noack, Was ist eigentlich eine 'Ruhemasse'?
• Norbert Dragon, Geometrie der Relativitätstheorie
• Wikibooks: Ruhemasse und relativistische Masse
• Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3

Quellen

1. ↑ Einstein schrieb in einem Brief an Lincoln Barnett, 19. Juni 1948:
   "Es ist nicht gut, von der Masse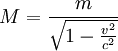 $M=\frac{m}{\sqrt{1-\frac{v^2}{c^2}}}$ eines bewegten Körpers zu sprechen, da von M keine klare Definition gegeben werden kann. Man beschränkt sich besser auf die "Ruhe-Masse" m. Daneben kann man ja den Ausdruck für momentum und Energie geben, wenn man das Trägheitsverhalten rasch bewegter Körper angeben will."
   Entnommen von Lev B. Okun: The Concept of Mass. (PDF, ca. 10MB) In: Physics Today. 42, Nr. 6, June 1989, S. 31–36
2. ↑ Whittaker, E. T.: 2. Edition: A History of the theories of aether and electricity, vol. 1: The classical theories / vol. 2: The modern theories 1900-1926. Nelson, London 1951-1953. 
3. ↑ Jannsen, M., Mecklenburg, M.: From classical to relativistic mechanics: Electromagnetic models of the electron. In: V. F. Hendricks, et.al. (Hrsg.): Interactions: Mathematics, Physics and Philosophy. Springer, Dordrecht 2007, S. 65–134. 
4. ↑ Born, M.: Die Relativitätstheorie Einsteins. Springer, Berlin-Heidelberg-New York 1964/2003, ISBN 3-540-00470-x. 
5. ↑ R. Stuewer, Mass-Energy and and the Neutron in the Early Thirties, in Einstein in Context: A Special Issue of Science in Context, Science in Context, Vol 6 (1993), S. 195 ff. Auszug in Google-books
6. ↑ K. T. Bainbridge, The Equivalence of Mass and Energy, Phys. Rev. 44 (1933), S. 123 - 123.
7. ↑ S. Rainville et al., A direct test of E=mc², Nature 438 (2005), S. 1096-1097. Abstract
8. ↑ Markus Pössel, Albert-Einstein-Institut: Von E=mc² zur Atombombe und Ist das Ganze die Summe seiner Teile?
9. ↑ Einstein, A.: Ist die Trägheit eines Körpers von dessen Energieinhalt abhängig?. In: Annalen der Physik. 18, 1905, S. 639-643. 
10. ↑ Darrigol, O.: The Genesis of the theory of relativity. In: Séminaire Poincaré. 1, 2005, S. 1-22.