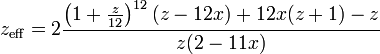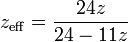- Effektivzinsmethode
-
Der effektive Jahreszins beziffert die jährlichen und auf die nominale Kredithöhe bezogenen Kosten von Krediten. Er wird in Prozent angegeben und müsste folglich eher effektiver Jahreszinssatz lauten, aber die Bezeichnung hat sich so eingebürgert. Bei Krediten, deren Zinssatz oder/und andere preisbestimmende Faktoren sich während der Laufzeit ändern (können), wird er als anfänglicher effektiver Jahreszins bezeichnet.
Der Effektivzinssatz wird im Wesentlichen vom Nominalzinssatz, dem Auszahlungskurs (Disagio), der Tilgung und der Zinsfestschreibungsdauer bestimmt.
Rahmenbedingungen für die Berechnung des effektiven Jahreszinssatzes
Mit Hilfe des Effektivzinssatzes können nur Darlehensangebote mit gleicher Zinsfestschreibungsdauer verglichen werden.
Wenn Faktoren wie insbesondere Tilgungsfreijahre, Tilgungsersatz, Art der Tilgungsverrechnung, Bearbeitungsgebühren und Darlehensgebühren in die Effektivzinssatzermittlung rechnerisch korrekt einbezogenen wurden, dann können sie bei verglichenen Darlehen durchaus unterschiedlich sein, denn die wichtigste Aufgabe der Effektivzinssatzberechnung besteht gerade darin, unterschiedlich gestaltete Kredite vergleichbar zu machen.
Im Effektivzinssatz sind keine Schätzgebühren (Taxkosten oder Wertermittlungsgebühren), Bereitstellungszinsen, Teilauszahlungszuschläge und Kontoführungsgebühren enthalten. Dies muss berücksichtigt werden, wenn eingeholte Angebote objektiv verglichen werden sollen. Der Effektivzinssatz berücksichtigt im Gegensatz zum Nominalzinssatz alle weiteren preisbestimmenden Faktoren aus dem regelmäßigen Kreditverlauf, d. h., der Effektivzinssatz gibt die Gesamtkosten des Darlehens pro Jahr in Prozent an. Preisbestimmende Faktoren sind Nominalzinssatz, Bearbeitungsgebühren, Auszahlungskurs, Tilgungssatz, -beginn und -höhe, Zins- und Tilgungsverrechnungstermine.
Vergleich unterschiedlich gestalteter Kredite und Anlagen
Neben der gesetzlich vorgeschriebenen Berechnung gibt es auch universell einsetzbare finanzmathematische Verfahren, die aus allen Einzahlungen in eine Anlage und Auszahlungen aus der Anlage unabhängig von Art und Benennung dieser Zahlungen einen Effektivzinssatz als Vergleichsmaß ermitteln, das sich ebenfalls als effektiver Jahreszinssatz ausdrücken lässt. Die Unabhängigkeit von Art und Benennung der betrachteten Ein- und Auszahlungen ist ein Vorteil dieser klassischen Verfahren der so genannten Rentenrechnung. Die dahinter stehende Mathematik der geometrischen Reihen ist relativ alt, war aber für frühere Preisangabenverordnungen nicht ausreichend einfach umsetzbar. Rechnerimplementiert können die nötigen (iterativen) Berechnungsverfahren heute jedoch problemlos eingesetzt werden. Für die reine Kosten- bzw. Renditeberechnung kann man solche Berechnungen sogar zum Vergleich sehr unterschiedlich gestalteter Kredite und Anlagen einsetzen, insbesondere bei einer nachträglichen Bewertung. Das ist besonders dann wichtig, wenn Kredite und Anlagen so gestaltet wurden, dass ein Vergleich mit anderen Finanzprodukten im Markt schwer fällt. Als Entscheidungshilfe bei Auswahl von Krediten und Anlagen misst auch dieser Effektivzinssatz aber nur einen Aspekt eines Kredits bzw. einer Anlage. Andere Aspekte wie Risiko, Sicherheit, Preisentwicklung usw. müssen zusätzlich bewertet werden.
Preisangabenverordnung
Der effektive Jahreszinssatz ist in § 492 Absatz 2 Satz 1 BGB vom Gesetz definiert. Nach Satz 2 dieser Norm hat die Berechnung des Effektivzinssatzes nach der Preisangabenverordnung (PAngV) zu erfolgen.
Das in der Verordnung vorgeschriebene Verfahren entspricht heute der Berechnung des internen Zinsfußes[1]. Es ist ein in der Rentenrechnung lange bekanntes Verfahren und wurde in Deutschland im Jahr 2000 auf Druck des EU-Ministerrats für Verbraucherfragen (1996) eingeführt. Im Gegensatz zur alten Methode[2] kann mit der heutigen Berechnungsmethode der Effektivzins nicht mehr so einfach durch Verteilung von Kreditkosten auf unterschiedlich gewichtete Kostenkategorien manipuliert werden.
Wegen der Schwächen der damaligen PAngV-Methode gab es damals bei den Banken Programme, bei denen zur internen Effektivzinsberechnung ein Verfahren[3] der damaligen AIBD (Standard Method of Calculating Yields for International Bonds, Association of International Bond Dealers, 1969-1992, Zürich) eingesetzt wurde. Gegenüber den Kunden musste aber der Effektivzinssatz nach der damaligen PAngV angegeben werden. Neben dem Interesse der Banken an durch Produktgestaltung manipulierbaren Zinsangaben[4][5] war ein weiterer Grund für deren Widerstand gegen die Anwendung des internen Zinsfußes, dass dieses Verfahren iterativ ist: Ein Rechner braucht für die Berechnung des internen Zinsfußes mehrere Durchläufe, bis die vorgeschriebene Genauigkeit erreicht wird. Aber schon in den 80er Jahren stand das Verfahren auch in Taschenrechnern und Tabellenkalkulationsprogrammen zur Verfügung.
Bei Verbraucherdarlehen gehört die Angabe des effektiven Jahreszinssatzes gemäß § 492 Absatz 1 Satz 5 Nr. 5 BGB zwingend zum Inhalt des Vertrages, um dem Verbraucher Zinsvergleiche zu ermöglichen. Zum Schutz des Verbrauchers ist im Gesetz zusätzlich festgelegt:
Fehlt die Angabe des effektiven oder anfänglichen effektiven Jahreszinses, mindert sich der Zinssatz gemäß § 494 Absatz 2 Satz 2 BGB auf den gesetzlichen Zinssatz (§ 246 BGB). Ist die Angabe im Vertrag zu niedrig (falsch), mindert sich der Zinssatz gemäß § 494 Absatz 3 BGB verhältnismäßig um den Prozentsatz, um welchen der effektive oder anfänglich effektive Jahreszins zu niedrig angegeben ist.
Missbräuchliche Verwendung
Der effektive Jahreszins ist eine Kenngröße, um unabhängige Kredite zu vergleichen. Ist das Darlehen fest mit dem Kauf eines Produktes verknüpft, wie beispielsweise beim Kauf eines Autos, so ist die vorrangige Kenngröße der Kaufpreis. Wird dieser nicht genannt, wie häufig in der Werbung, so ist die Angabe des effektiven Jahreszinssatzes irrelevant. Um verschiedene Finanzierungen eines Produktes zu vergleichen, müsste anhand eines angenommenen effektiven Jahreszinssatzes und der Zahlungsraten der effektive Kaufpreis bestimmt werden.
Berechnung des effektiven Jahreszins nach der Uniform-Methode
Die einfachste Art zur Berechnung des ungefähren effektiven Jahreszins ist die Uniform-Methode:
Kreditkosten = gesamte Rückzahlung - Auszahlungsbetrag oder Anzahl der Raten * Ratenbetrag - Auszahlungsbetragdazu gehören:
- Restschuldversicherung bzw. Kreditlebensversicherung
- Bearbeitungsgebühr
- Zinsen
Nettodarlehensbetrag = Darlehensnennbetrag - Kreditkosten
Anwendungsbereich
Die Uniform-Methode ermöglicht bei bestimmten Darlehensarten eine Abschätzung des Effektivzinssatzes. Rechtlich gültig und von Finanzdienstleistern auszuweisen ist die komplizierter zu berechnende, aber genauere Effektivverzinsung nach PAngV. Die Uniform-Methode ist als überschlägige Berechnung anzusehen, mit der man insbesondere bei mit gleichen Monatsraten zu tilgenden Krediten schnell einen Eindruck von dem zu erwartenden tatsächlichen Effektivzins erhalten kann. Das Ergebnis kann von der PAngV-Effektivverzinsung abweichen.
Beispiel
Ein Verbraucherkredit über 10.000,00 EUR wird aufgenommen. Der Zinssatz beträgt 0,5% pro Monat und bezieht sich während der gesamten Laufzeit auf die Ursprungssumme von 10.000,00 EUR, die Laufzeit liegt bei 60 Monaten. Zur Bereitstellung werden 3% Bearbeitungsgebühr erhoben. Die Bearbeitungsgebühr wird bei Kreditaufnahme entrichtet, bereitgestellt werden die vollen 10.000,00 EUR.
Kreditkosten = Zinsen + Bearbeitungsgebühr = 0,50% · 10.000,00 EUR · 60 Monate + 3 % · 10.000,00 EUR = 3.300,00 EUR (0,005*10000*60 + 0,03*10000 = 3300€)
Anm.: Zinsen und Tilgung werden monatlich gezahlt, aber der Kreditbetrag gilt erst am Ende der Laufzeit als komplett getilgt, d. h. monatlich wird eine Rate von 3.300€/60 + 10.000€/60 = 55€ + 166,67€ = 221,67€ fällig.
eff. Jahreszinssatz = 3.300,00 EUR · 24 / ((60 + 1) · 10.000,00 EUR) · 100 = 12,983607.
Der eff. Zinssatz (Jahreszinssatz) errechnet sich durch die Zinsung aller Einnahmen und Ausgaben auf einen Zinszeitpunkt mit dem Ergebnis „Null“. Dann entsprechen sich gezinst alle Einnahmen und Ausgaben. Unter Annahme der Auszahlung in Höhe von 10.000€ und der Gebühr in Höhe 300€ zum Auszahlungszeitpunkt sowie 60 Monatsraten in Höhe von 221,67€ beginnend mit dem Auszahlungszeitpunkt ergibt sich ein eff. Zinssatz von 14,5950%. Sofern die Ratenzahlungen einen Monat später beginnen, ist der eff. Zinssatz 14,0221%. Der jeweils zu ermittelnde gezinste Betrag wird wie folgt errechnet: Betrag x (1 + Zinssatz) ^ „Zeit in Jahren“, wobei „Zeit in Jahren“ ein Teilwert sein kann und auch ein negativer Wert.
Berechnung des eff. Jahreszinssatzes bei Anleihen
Den effektiven Jahreszinssatz bei endfälligen Anleihen, die über mehrere Jahre laufen und den Zins wieder mitverzinsen (Zinseszins), berechnet man mit Zinsfaktoren:
Bsp.: Eine Anleihe läuft 3 Jahre und wird mit 1,5 % im ersten, 2 % im zweiten und 3 % im dritten Jahr verzinst.
Bei Anleihen wird oft mit der Näherungsformel mit Auf- (Agio) und Abschlägen (Disagio) gerechnet:
(Diese Formel weicht bei kleinen Werten für Laufzeit und Agio/Disagio kaum vom korrekten Ergebnis ab, versagt aber bei entsprechend großen Werten.)
Allerdings handelt es sich bei dem Faktor
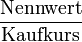 lediglich um einen weiteren Zinsfaktor, mit dem dann eine präzisere Formel konstruiert werden kann:
lediglich um einen weiteren Zinsfaktor, mit dem dann eine präzisere Formel konstruiert werden kann:Berechnung des eff. Jahreszinssatzes bei Krediten mit festen monatlichen Raten
Die folgende Berechnungsvorschrift wird für Kredite hergeleitet, für die weder einmalige Zuschläge (Bearbeitungsgebühren) noch Abschläge (Disagio) vereinbart sind.
Der von der Bank üblicherweise angegebene Zinssatz ist eigentlich überhaupt kein Jahreszinssatz, sondern das Zwölffache eines "effektiven Monatszinssatzes". Nach jedem Monat – bzw. nach jedem Zwölftel des Jahres – wird folglich saldiert und neu gerechnet. Der Zinseszinseffekt tritt also bereits nach dem ersten Monat auf, und dies führt dazu, dass unter den für diesen Abschnitt genannten Bedingungen der effektive Jahreszinssatz immer höher ist als der von der Bank genannte Zinssatz.
Zur Herleitung der Berechnungsvorschrift stellen wir die Bildung der monatlichen bzw. jahresendlichen Kontobeträge für monatliche und jahresendliche Saldierung einander gegenüber. Folgende Größen spielen dabei eine Rolle:
G0 = Schuld zu Beginn des Jahres R = monatliche Rate, die Zins und u.U. auch Tilgung enthält z = Bankzinssatz zeff = effektiver Jahreszinssatz Für den von der Bank genannten Zinssatz gilt nach i Monaten:
Für den effektiven Jahreszinssatz gilt nach einem Jahr (in Gegenüberstellung zu obiger Formel für i = 12):
Der Subtrahend ergibt sich zum einen aus den Raten, die innerhalb des Jahres keine Zinszahlungen enthalten - da ein effektiver Jahreszinssatz nur am Jahresende angewendet wird -, und aus der Verzinsung dieser vor dem Jahresende geleisteten Raten bis zum Ende des Jahres: Die erste liegt elf Monate an, die zweite zehn usw. und die letzte wird genau zum Jahresende geleistet und erzielt deshalb keine Verzinsung. Diese Verzinsung muss dem Tilgenden ebenfalls gutgeschrieben werden.
Gleichsetzung beider Formeln für G12 und Austausch von R durch x G0 liefert schließlich für zeff folgende Formel:
Die Berechnung des effektiven Jahreszinssatzes ist also nicht nur vom Bankzinssatz, sondern auch von der Geschwindigkeit der Tilgung abhängig, also vom Verhältnis zwischen R und G0. Stark vereinfacht wird die Formel, wenn keine Tilgung erfolgt, sondern die Raten nur die fälligen Zinsen begleichen. Dann wird x = z / 12, und daraus folgt:
Diese Formel mag unglaubwürdig erscheinen, weil sie für z = 24 / 11 nicht definiert ist und für noch höhere Werte z sogar unsinnige negative Ergebnisse liefert. Man muss sich jedoch klar machen, was es heißt, einen Bankzinssatz von 218 % präsentiert zu bekommen. Innerhalb von sechs Monaten wird über die monatlichen Beträge eine größere Summe gezahlt, als die Schuldsumme vom Jahresanfang ausmacht. Nach der Vorgehensweise des effektiven Jahreszinssatzes bedeutet dies, dass der Schuldner, der ja während des Jahres keine Zinsen zahlt, sondern nur tilgt, ab dem sechsten Monat ein Guthaben bei der Bank bildet. Dieses Guthaben muss die Bank natürlich ebenso verzinsen wie zuvor die Schuld - nur mit umgekehrtem Vorzeichen. Beide Zinsen werden gegeneinander aufgerechnet und müssen ohne jegliche Tilgung den Wert null ergeben. Das kann aber nicht funktionieren, wenn die Schuldsumme vom Jahresanfang bereits vor der Jahreshälfte getilgt worden ist. Folglich müssen die Zinsen auf die im Laufe statt am Ende des Jahres gezahlten Raten den Ausschlag geben. Und dazu müssen sie eben sehr hoch sein - im Extremfall unendlich.
Für Zinssätze in normalen Größenordnungen liefert die Formel jedoch nicht nur (ebenfalls) korrekte, sondern zudem einleuchtende Ergebnisse. Wird eine Schuldsumme von 100 Euro innerhalb eines Jahres getilgt, wobei ein Bankzinssatz von 10 % angesetzt wird, so ergibt sich der effektive Jahreszinssatz zu 10,65 %. Soll die Schuld bei gleichem Bankzinssatz nur gehalten werden, so beläuft sich der effektive Jahreszinssatz auf 10,48 %
Links
- Lernzettel zur Investitionsrechnung
- Die zeitliche Kapitalbindung als Grundlage zur Analyse von Investitionen
- Interaktive Berechnung mit Beispielen (in Javascript)
Quellen
- ↑ http://gaya.scienza.de/INVESTOR.HTM#Zinsfuss
- ↑ http://gaya.scienza.de/INVESTOR.HTM#PAngV
- ↑ http://gaya.scienza.de/aibd.htm
- ↑ Capital 2/1985, "Blinde Kuh", S.34-35
- ↑ test 4/1987, "Verbraucherschutz ausgetrickst"
Literatur
- Wolfgang Lücke: Investitionslexikon, 1991, ISBN 3800611945
- Konrad Wimmer: So rechnen Banken, 2000, ISBN 3423508221
Bitte beachte den Hinweis zu Rechtsthemen!
Wikimedia Foundation.


![\text{eff. Jahreszinssatz} = \left[ \left( \prod_{i=1}^\mathrm{Laufzeit}\left(1 + \frac{\%\mathrm{Zinssatz}_i}{100\%}\right) \right)^\frac{1}{\mathrm{Laufzeit}} - 1\right] \cdot 100\%](/pictures/dewiki/99/c8c30b4f93dc95807100a8aed2a9f72b.png)
![\mathrm{eff.\ Jahreszinssatz} = \left[ \left( (1+\frac{1{,}5\%}{100\%}) \cdot (1 + \frac{2\%}{100\%}) \cdot (1 + \frac{3\%}{100\%}) \right)^\frac{1}{3} - 1 \right] \cdot 100\%](/pictures/dewiki/49/11a3f5faa568c0542481eb352178c533.png)
![= \left[ ( 1{,}015 \cdot 1{,}02 \cdot 1{,}03 )^\frac{1}{3} - 1 \right] \cdot 100\%](/pictures/dewiki/99/cf36d210dd6356ad45fb077e0b495722.png)
![= \left[ \sqrt[3]{1{,}06636} - 1 \right] \cdot 100\%](/pictures/dewiki/100/db6e6341564e880948f0af0ff9bd68f3.png)
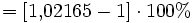
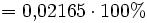
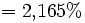
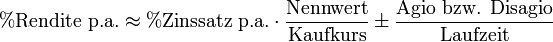
![\text{eff. Jahreszinssatz} = \left[ \left( \frac{\mathrm{Nennwert}}{\mathrm{Kaufkurs}} \prod_{i=1}^{\mathrm{Laufzeit}}\left( 1 + \frac{\%\mathrm{Zinssatz}_i}{100\%}\right) \right)^\frac{1}{\mathrm{Laufzeit}} - 1 \right] \cdot 100\%](/pictures/dewiki/57/98245048d1fcfcac4003e8e7fafdd1ef.png)
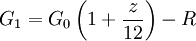
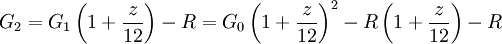
![G_3 = G_0 \left(1 + \frac{z}{12}\right)^3 - R \left[\left(1 + \frac{z}{12}\right)^2 + \left(1 + \frac{z}{12}\right) + 1\right]](/pictures/dewiki/53/5bf4862180a0126c5c8dc7539b6db442.png)
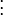
![G_{12} = G_0 \left(1 + \frac{z}{12}\right)^{12} - R \left[\left(1 + \frac{z}{12}\right)^{11} + \left(1 + \frac{z}{12}\right)^{10} + \cdots + \left(1 + \frac{z}{12}\right) + 1\right]](/pictures/dewiki/101/e287c5e1e3cd3296317bed7710414978.png)
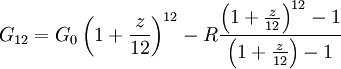
![G_{12} = G_0 \left(1 + \frac{z}{12}\right)^{12} - \frac{12 R}{z} \left[\left(1 + \frac{z}{12}\right)^{12} - 1\right]](/pictures/dewiki/101/eb4c3ae60a6e0926a5222fa178cb275a.png)
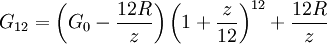
![G_{12} = G_0 \left(1 + z_{\mathrm{eff}}\right) - R \left[12 + \left(\frac{1}{12} + \frac{2}{12} + \cdots + \frac{11}{12} \right) z_{\mathrm{eff}}\right]](/pictures/dewiki/101/eaa863fa1bf2472d7f5f423f6ad3a712.png)